Bestimme bei folgenden Funktionen die Schnittpunkte mit den Koordinatenachsen.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte mit den Koordinatenachsen
Um die Schnittpunkte mit den Koordinatenachsen zu berechnen, wird eine der Variablen in der Funktion (, ) gleich gesetzt.
Schnittpunkte mit der x-Achse
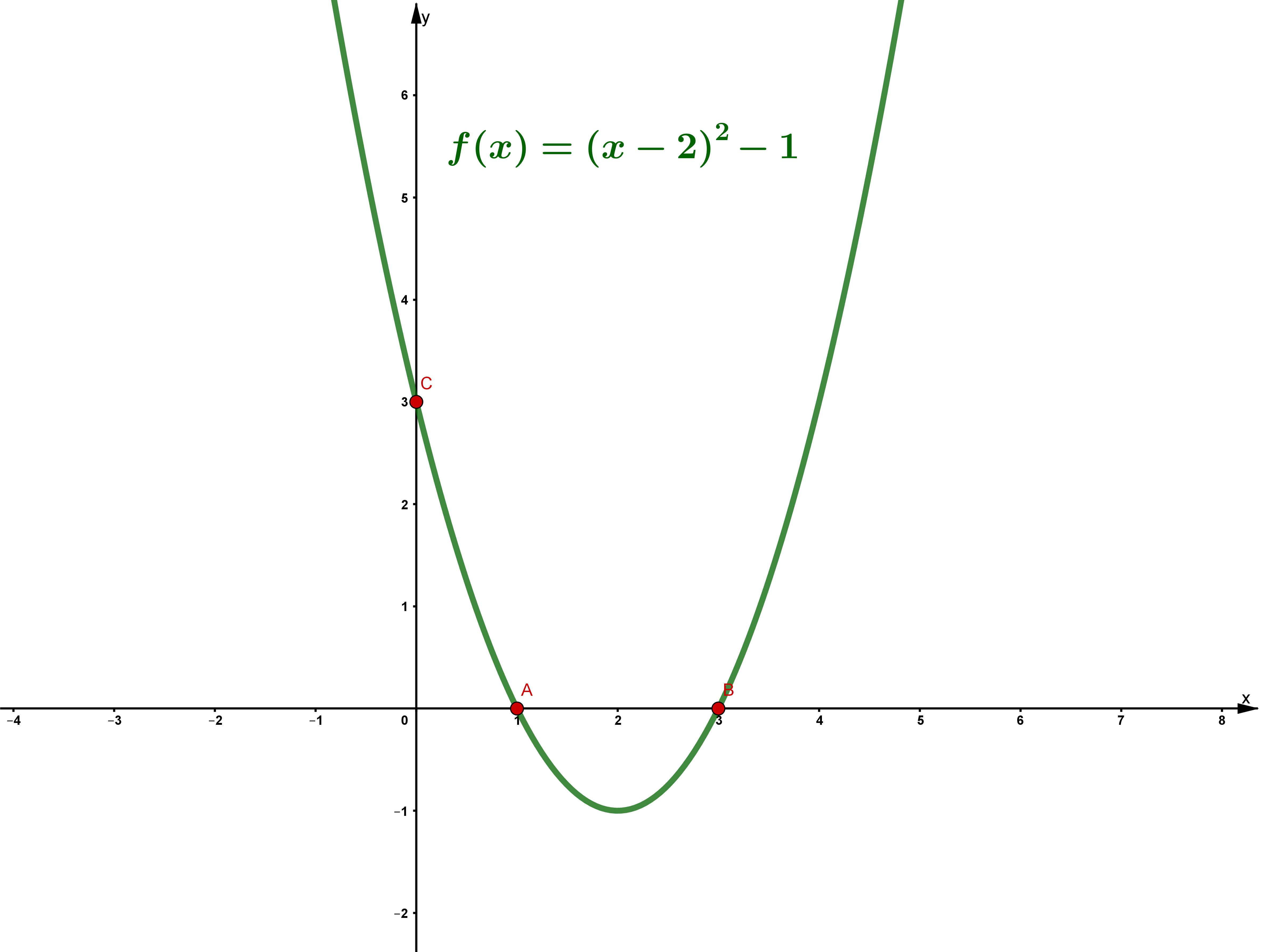
Die Schnittpunkte mit der -Achse sind die Nullstellen der Funktion.Man erhält sie, indem man die Funktion bzw. den -Wert gleich Null setzt.
Die Schnittpunkte mit der -Achse liegen bei und .
Schnittpunkt mit der y-Achse
Um den Schnittpunkt mit der -Achse zu ermitteln, muss für den -Wert eingesetzt werden.
Der Schnittpunkt mit der -Achse liegt bei .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte mit den Koordinatenachsen
Um die Schnittpunkte mit den Koordinatenachsen zu berechnen, wird eine der Variablen in der Funktion (, ) gleich gesetzt.
Schnittpunkte mit der x-Achse
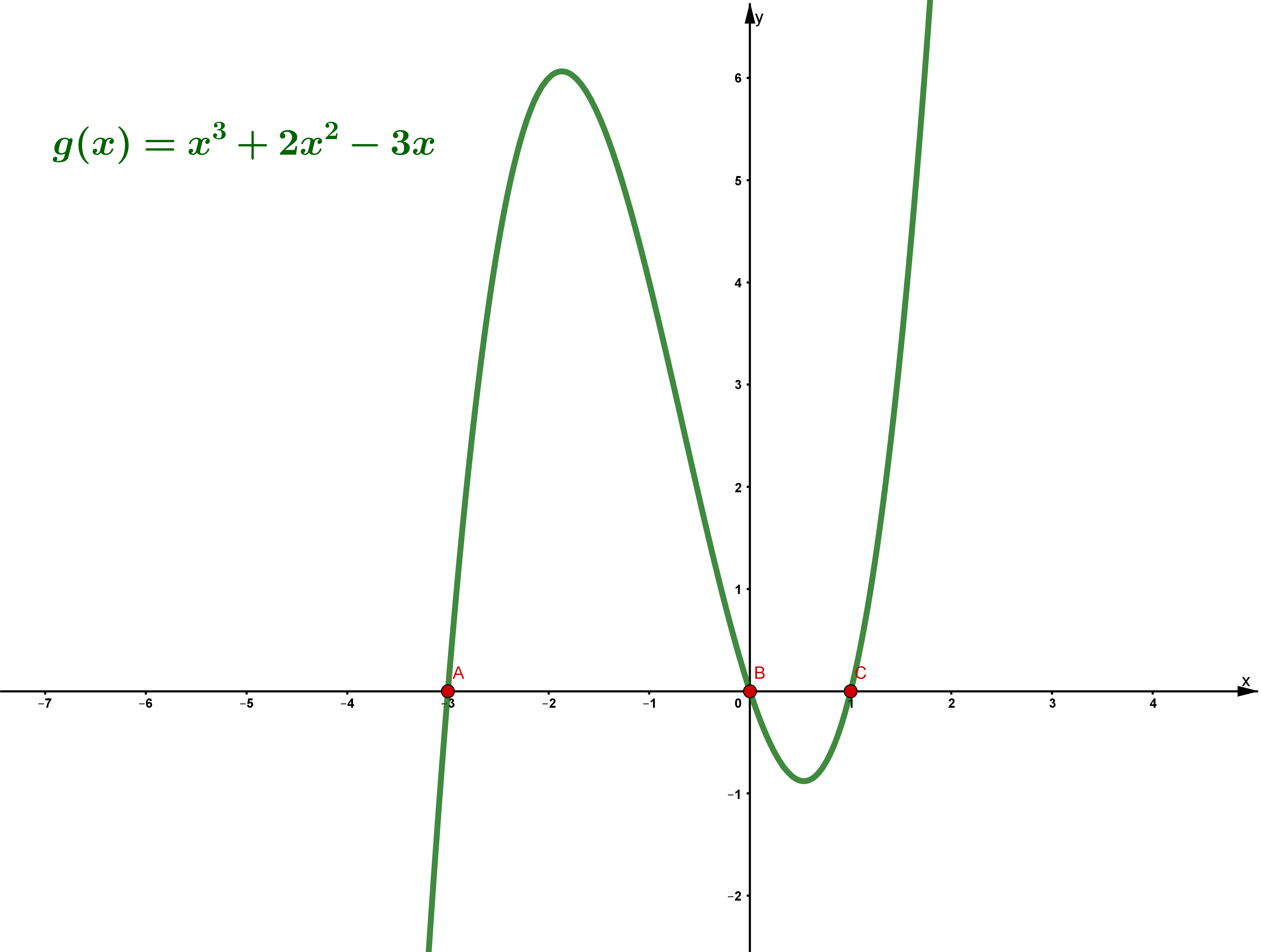
Die Schnittpunkte mit der -Achse sind die Nullstellen der Funktion.Man erhält sie, indem man die Funktion bzw. den -Wert gleich Null setzt.
↓ Kleinste Potenz von ausklammern.
↓ Ein Produkt wir dann Null, wenn einer der Faktoren Null ist.
Setze die Klammer gleich Null.
↓ Mitternachtsformel anwenden.
Die Schnittpunkte mit der -Achse liegen bei und und .
Schnittpunkt mit der y-Achse
Um den Schnittpunkt mit der -Achse zu ermitteln, muss für den -Wert eingesetzt werden.
Der Schnittpunkt mit der -Achse liegt bei .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte mit den Koordinatenachsen
Um die Schnittpunkte mit den Koordinatenachsen zu berechnen, wird eine der Variablen in der Funktion (, ) gleich gesetzt.
Schnittpunkte mit der x-Achse
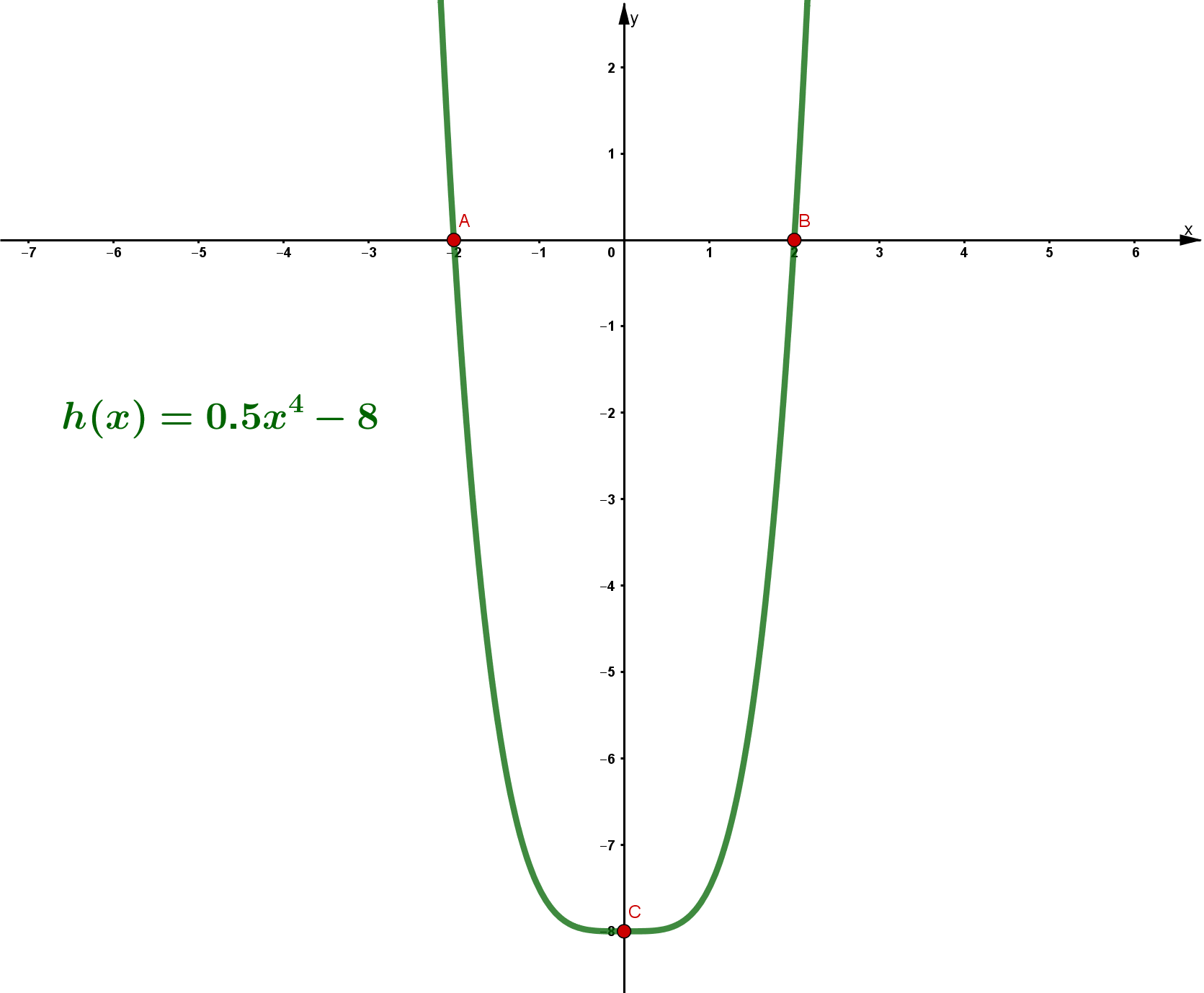
Die Schnittpunkte mit der -Achse sind die Nullstellen der Funktion.Man erhält sie, indem man die Funktion bzw. den -Wert gleich Null setzt.
Die Schnittpunkte mit der -Achse liegen bei und .
Schnittpunkt mit der y-Achse
Um den Schnittpunkt mit der -Achse zu ermitteln, muss für den -Wert eingesetzt werden.
Der Schnittpunkt mit der -Achse liegt bei .
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
