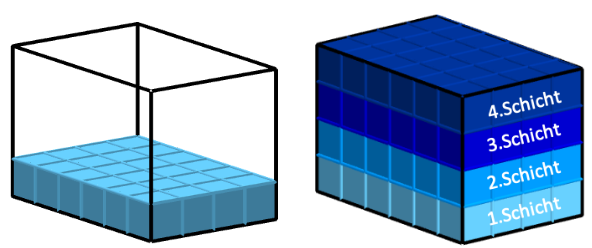
1 Übersicht
Inhalt des Kurses
Thema dieses Kurses ist das Volumen eines Quaders und das Volumen eines Würfels. Dabei wird dir erst gezeigt, wie du Rauminhalte mit Hilfe von Einheitswürfeln messen kannst und anschschließend wie du Rauminhalte auch direkt berechnen kannst.
Vorkenntnisse
Zur Bearbeitung des Kurses sollten dir folgende Themen bekannt sein:
Kursdauer
Der Kurs dauert etwa Minuten wenn du die Übungsaufgaben selbständig bearbeitest.
2 Der Weihnachtsmann und der Nikolaus
Der Weihnachtsmann erhält dieses Jahr Hilfe vom Nikolaus beim Austeilen der Weihnachtsgeschenke. Als Erstes sollen die Kinder im Dorf "Mathehausen" beschenkt werden.

Als sie sich die Wunschliste der Kinder anschauen, fällt ihnen auf, dass alle Kinder sich nur das neue Brettspiel "Mathenopoly" wünschen. Um die Geschenke auszuteilen, stehen ihnen zwei Boxen zur Wahl:
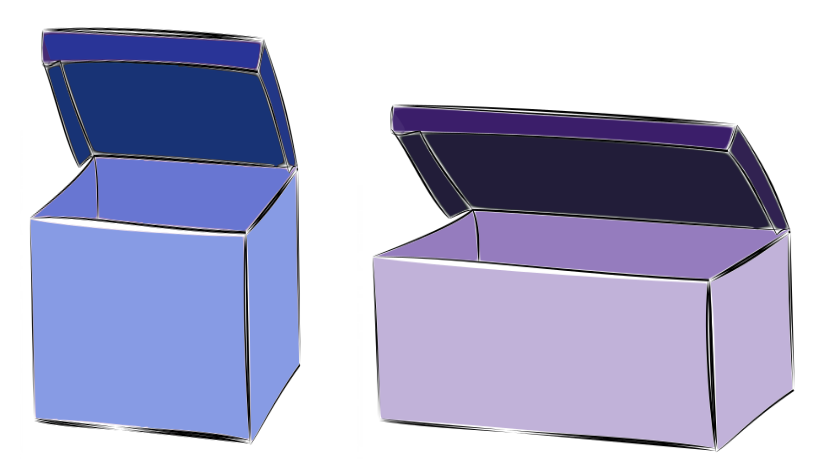
Der Weihnachtsmann möchte die linke Box nehmen, die ist nämlich größer, behauptet er.
Der Nikolaus ist da ganz anderer Meinung. Er behauptet die rechte Box sei größer.
Wer hat denn recht?
3 Erster Versuch: Direkter Vergleich
Der Weihnachtsmann und der Nikolaus legen beide Boxen nebeneinander hin, um zu sehen, welche nun größer ist.

Sie versuchen eine Box in die andere hineinzubringen. Das klappt aber nicht.

Da sie sich immer noch nicht einig sind, suchen sie nach einer neuen Methode, um entscheiden zu können, welche Box größer ist.
4 Zweiter Versuch: Auslegen mit Geschenken
Die Boxen sollen genutzt werden, um Geschenke zu transportieren. Die größere Box sollte also die sein, in der am meisten Geschenke reinpassen. Daher füllen beide ihre Boxen mit den "Mathenopoly" Geschenken und zählen dann wie viele reinpassen.
Zum Austeilen der Geschenke macht es also keinen Unterschied aus, ob die linke Box oder die rechte Box gewählt wird. Der Nikolaus ist aber dennoch nicht ganz überzeugt:

Um Rauminhalte von Quadern genau messen zu können, ist das Auslegen mit "Mathenopoly" Geschenke wohl nicht die beste Methode. Ein kleineres Objekt mit einer ganz bestimmten Form wird gebraucht: Der Einheitswürfel. Bevor dir der Einheitswürfel vorgestellt wird, erhältst du noch kurz einen Überblick über Würfel und Quader.
5 Würfel und Quader
Im Folgenden erhältst du einen kurzen Überblick über die beiden Körper Würfel und Quader und deren Merkmale.
Würfel
Ein Würfel ist ein dreidimensionaler Körper.
Er besitzt folgende Merkmale:
12 gleich lange Kanten
6 quadratische Seiten, die gleich groß sind
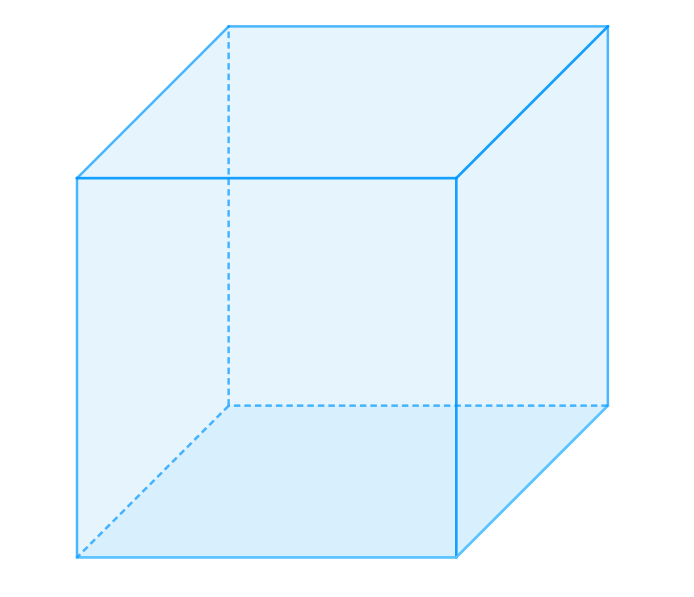
Quader
Ein Quader ist ein dreidimensionaler Körper. Er besitzt folgende Merkmale:
6 rechteckige Seiten
Die gegenüberliegende Seiten sind deckungsgleich
12 Kanten, von denen jeweils 4 gleich lang sind
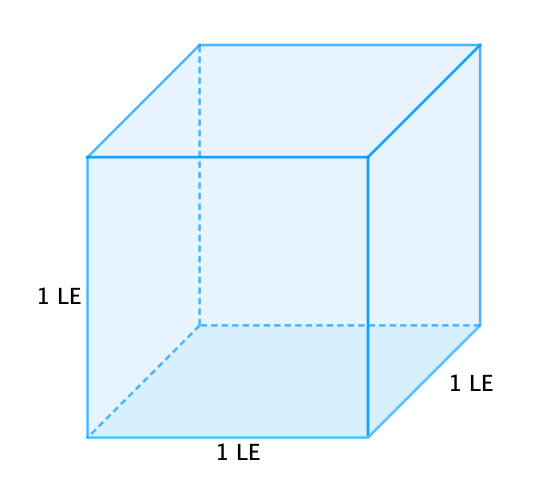
6 Einheitswürfel
Ein Würfel der Kantenlänge 1 Längeneinheit (kurz: 1 LE) wird als Einheitswürfel bezeichnet.
Achte darauf: Je nach Aufgabenstellung kann 1 LE unterschiedliche Längen entsprechen (zum Beispiel 1 cm, 1 m…).
Wozu brauchst du eigentlich den Einheitswürfel? Auf den folgenden Kursseiten werden dir zwei verschiedene Methoden vorgestellt. Dabei benutzt du die Hilfe von Einheitswürfeln, um Volumina von Würfel und Quader zu bestimmen.
7 Messen von Rauminhalten (1/2)
Auslegen mit Einheitswürfel
Du kannst den Rauminhalt einiger einfacher Körper schätzen, indem du diese mit Einheitswürfeln auslegst. Beim Platzieren der Einheitswürfel ist zu beachten, dass der Rauminhalt möglichst komplett ausgefüllt wird.
Beispiel 1: Würfel
Im folgenden Beispiel wird dir gezeigt, wie du das Volumen eines Würfels schätzen kannst, in dem du diesen mit Einheitswürfeln auslegst.
Im nebenstehenden Bild siehst du einen Würfel, dessen Volumen du schätzen sollst. Neben dem Würfel ist ein blauer Einheitswürfel abgebildet.
In den nächsten Schritten legst du nun nacheinander Einheitswürfel in den größeren Würfel, um dessen Volumen schätzen zu können.
Zunächst wird ein Einheitswürfel in den Würfel gelegt.
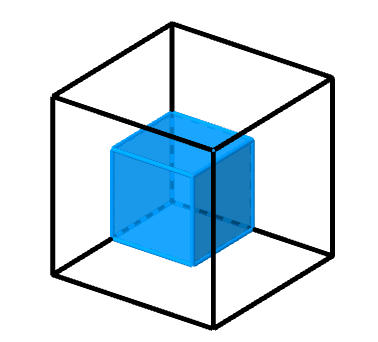
In diesem Bild sind bereits 3 Einheitswürfel in dem großen Würfel enthalten.
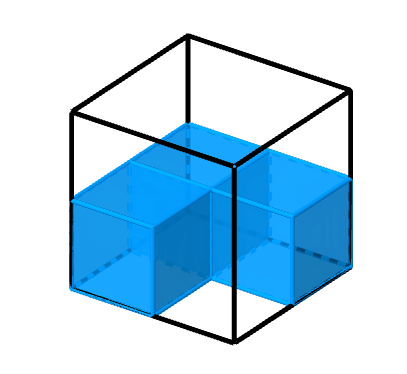
Der Würfel ist nun komplett mit Einheitswürfeln ausgefüllt. Dies erhältst du, in dem du das Schema der vorherigen Bilder fortsetzt.

Um die Gesamtlösung zu erhalten, zählst du nun die einzelnen Einheitswürfel. In der unteren Schicht des Würfels befinden sich 4 Einheitswürfel. Weitere 4 Einheitswürfel sind in der oberen Schicht des Würfels zu sehen. Zusammengezählt passen 8 Einheitswürfel in den großen Würfel.
8 Messen von Rauminhalten (2/2)
Beispiel 2: Quader
Im folgenden Beispiel wird dir gezeigt, wie du das Volumen eines Quaders schätzen kannst, in dem du diesen mit Einheitswürfeln auslegst.
Im nebenstehenden Bild siehst du einen Quader, dessen Volumen du schätzen sollst. Neben dem Quader ist ein Einheitswürfel abgebildet.
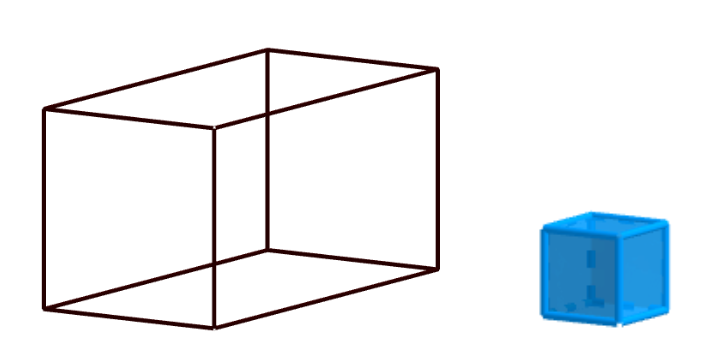
In den nächsten Schritten legst du nun nacheinander Einheitswürfel in den Quader, um dessen Volumen schätzen zu können.
Zunächst wird ein Einheitswürfel in den Quader gelegt.
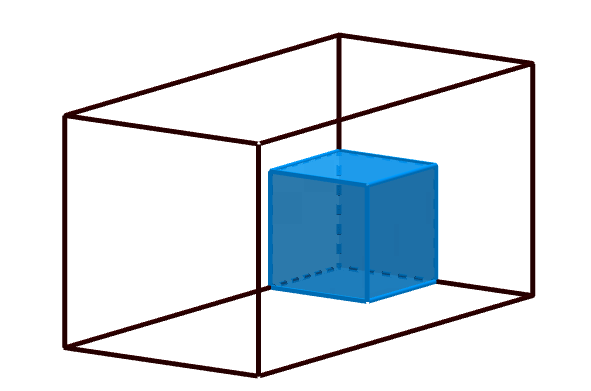
Im rechten Bild sind bereits 5 Einheitswürfel in dem Quader enthalten.
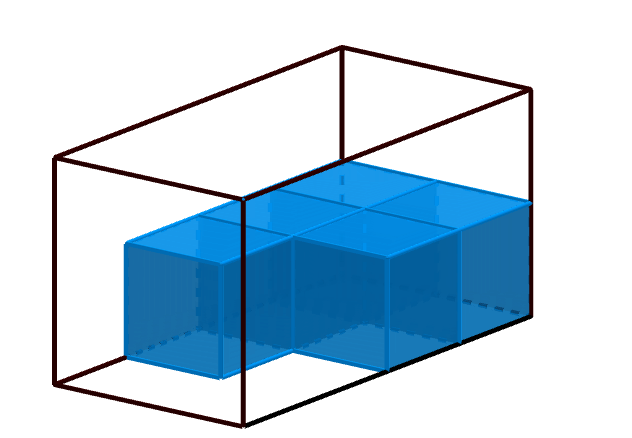
Der Quader ist nun komplett mit Einheitswürfeln ausgefüllt. Dies erhältst du, in dem du das Schema der vorherigen Bilder fortsetzt.
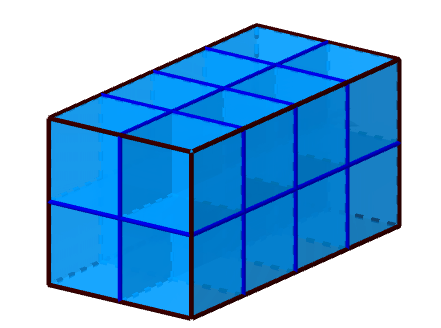
Um die Gesamtlösung zu erhalten, zählst du nun die einzelnen Einheitswürfel. In der unteren Schicht des Quaders befinden sich 8 Einheitswürfel. Weitere 8 Einheitswürfel sind in der oberen Schicht des Quaders zu sehen. Zusammengezählt passen 16 Einheitswürfel in den Quader.
9 Aufgaben
Laden
Laden
10 Volumen eines Quaders
Auf der vorherigen Kursseite wurde dir gezeigt, wie du das Volumen eines Quaders schätzen kannst. Dabei hast du zunächst gezählt, wie viele Einheitswürfel sich in der unteren Schicht befinden. Danach hast du die Anzahl der Schichten gezählt.
Die Anzahl der Einheitswürfel in einer Schicht ergibt sich aus der Anzahl der Einheitswürfel in einer Reihe mal der Anzahl der Reihen.
Daraus folgt:
Anzahl der Einheitswürfel in einer Reihe Anzahl der Reihen Anzahl der Schichten
Die Anzahl der Einheitswürfel in einer Reihe entspricht der
Die Anzahl der Reihen entspricht der
Die Anzahl der Schichten entspricht der
Die Formel für das Volumen eines Quaders lautet also:
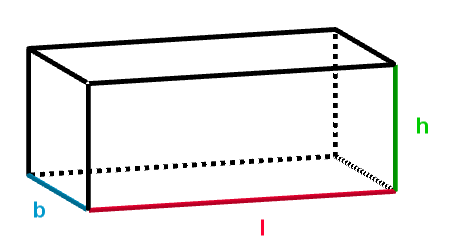
11 Beispielaufgabe zum Volumen eines Quaders
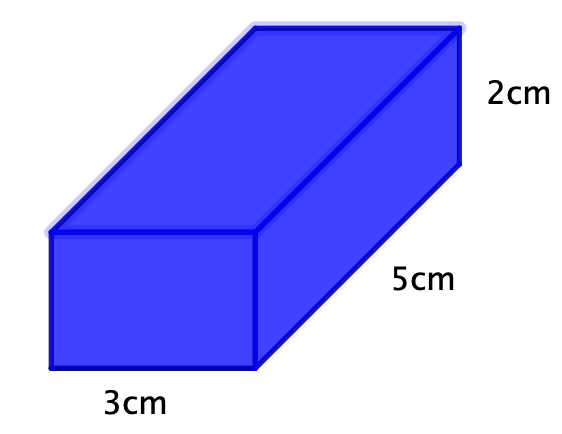
In der nebenstehenden Skizze ist ein Quader mit folgenden Maßen abgebildet:
Länge:
Breite:
Höhe:
Berechne das Volumen vom Quader.
Lösung
Das Volumen kannst du berechnen, indem du die Formel für das Volumen eines Quaders anwendest:
Die Maße für , und einsetzen.
Der Quader hat ein Volumen von .
12 Volumen eines Würfels
Der Würfel ist ein spezieller Quader bei dem die Länge, die Breite und die Höhe den gleichen Wert haben. Dieser Wert entspricht der des Würfels.
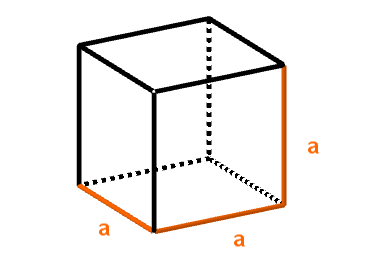
Die Formel für das Volumen eines Würfels lautet also:
Oder in der Potenzschreibweise:
13 Beispielaufgabe zum Volumen eines Würfels
In der nebenstehenden Skizze ist ein Würfel der Kantenlänge abgebildet. Berechne das Volumen des Würfels.
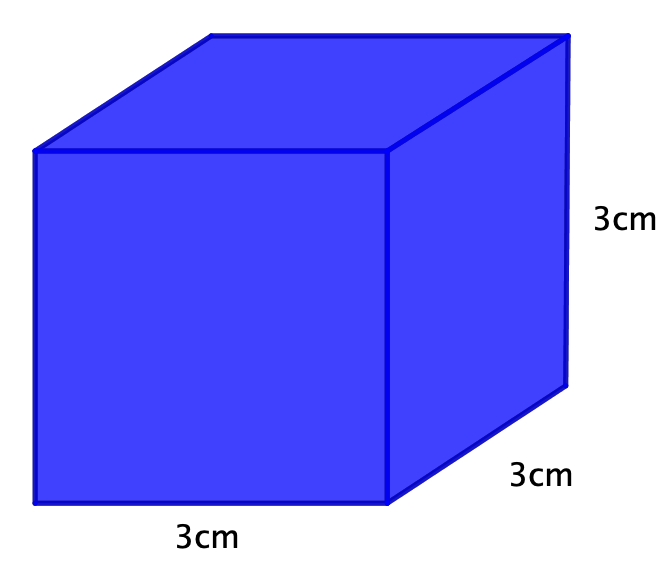
Lösung
Das Volumen eines Würfels kannst du mit Hilfe der Kantenlänge wie folgt berechnen:
einsetzen
Der Würfel hat ein Volumen von .
14 Aufgaben
Laden
Laden
15 Exkurs (1/2): zusammengesetzte Körper
Das Volumen eines Körpers, der aus verschiedenen Quadern besteht, kannst du ausrechnen, indem du die Volumina der Quader einzeln ausrechnest und diese dann zusammen addierst.
Beispiel
In der Skizze rechts wird ein Körper abgebildet. Dieser besteht aus einem Quader mit den Maßen:
Und einem Würfel mit der Kantenlänge .
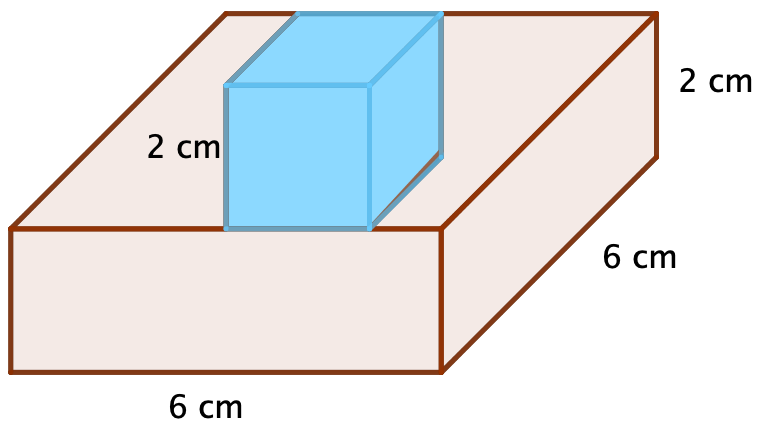
Das Volumen des Quaders lautet:
Das Volumen des Würfels lautet:
Das Gesamtvolumen berechnest du, indem du beide Volumina addierst:
Das Gesamtvolumen des Körpers beträgt also .
16 Exkurs (2/2): Ausschneiden
Wenn aus einem Körper ein Quader ausgeschnitten wird, kannst du das Volumen berechnen, indem du das Volumen des ausgeschnittenen Quaders vom Volumen des Körpers abziehst.
Beispiel
Bei der nebenstehenden Skizze wird ein Würfel von einem Quader ausgeschnitten. Die Maße des Quaders und des Würfels sind die gleichen wie beim vorherigen Beispiel. Somit ist:
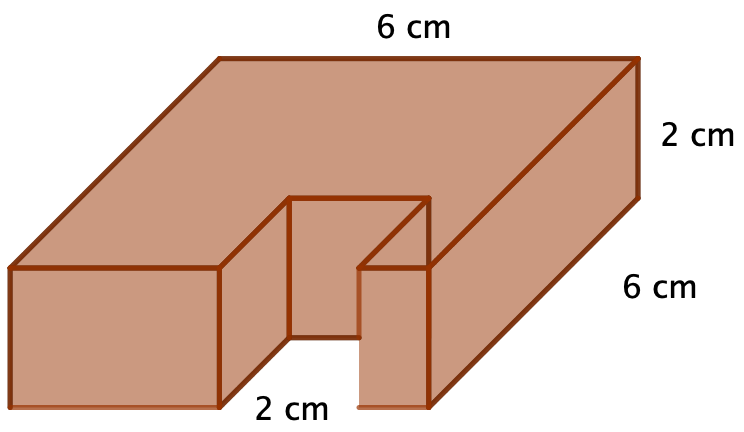
Das Gesamtvolumen berechnest du, indem du das Volumen des Würfels von dem Volumen des Quaders abziehst:
Das Gesamtvolumen dieses Körpers beträgt also .
17 Aufgaben zum Exkurs
Laden
Laden
18 Zusätzliche Knobelaufgabe zum Exkurs
Laden