Ein Rechteck ist ein Viereck, bei dem alle Innenwinkel 90° betragen.
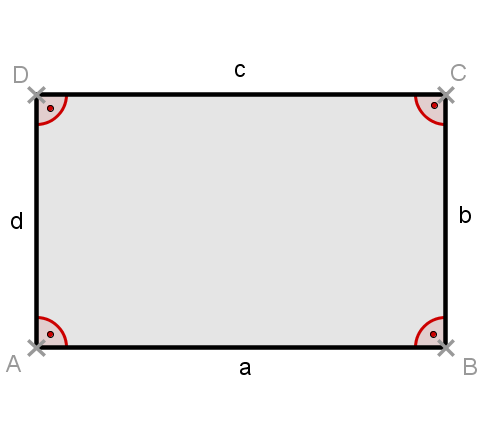
Fläche und Umfang
Flächeninhalt
Die Fläche eines Rechtecks ist das Produkt zweier beliebig aneinander liegender Seiten:
Oft sagt man auch:
Umfang
Der Umfang eines Rechtecks ist die Summe der Seitenlängen. Da die gegenüberliegenden Seiten stets gleich lang sind, also und ist der Umfang:
Weitere Eigenschaften des Rechtecks
Besonderheiten bei Seiten, Winkeln und Diagonalen
In einem Rechteck sind gegenüberliegende Seiten immer gleich lang:

In einem Rechteck betragen alle Winkel 90°:

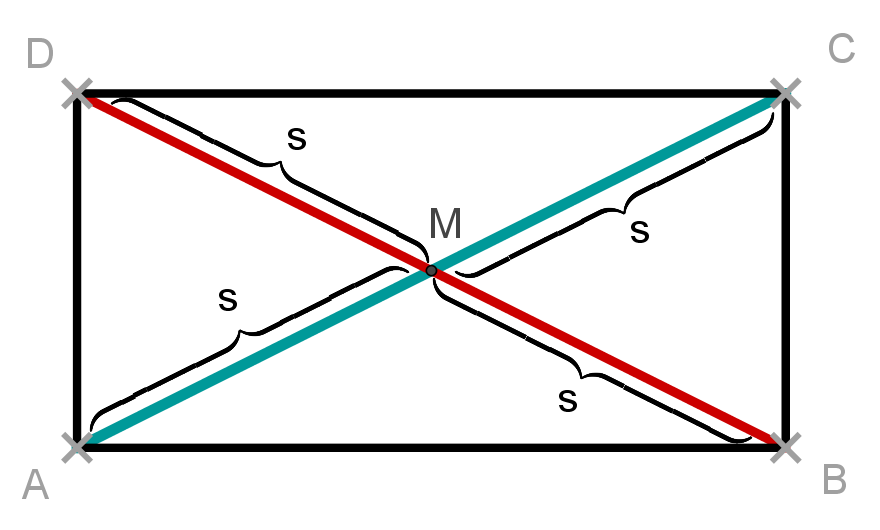
In einem Rechteck
sind die Diagonalen gleich lang.
halbieren sich die Diagonalen gegenseitig.
Einordnung als Viereck
Jedes Rechteck ist auch ein Parallelogramm.
Jedes Rechteck ist auch ein symmetrisches Trapez.
Spezialfälle von Rechtecken
Wenn ein Rechteck vier gleich lange Seiten hat, ist es ein Quadrat
Eine übersichtliche Einordnung des Rechtecks findest du im Haus der Vierecke.
Symmetrieeigenschaften
Punktsymmetrie Jedes Rechteck ist punktsymmetrisch zum Schnittpunkt seiner Diagonalen.
Achsensymmetrie Jedes Rechteck ist achsensymmetrisch und hat (mindestens) zwei Symmetrieachsen, nämlich die Mittelsenkrechten der Seiten.
Wenn ein Rechteck auch symmetrisch zu den Diagonalen ist, also vier Symmetrieachsen hat, ist es ein Quadrat.
Umkreis und Inkreis
Jedes Rechteck hat einen Umkreis, aber nicht unbedingt einen Inkreis.
Umkreis | Inkreis |
|---|---|
Jedes Rechteck hat einen Umkreis, nämlich den Thaleskreis über der Diagonalen. | Ein Rechteck hat im Allgemeinen keinen Inkreis. Die Ausnahme ist das Quadrat. |
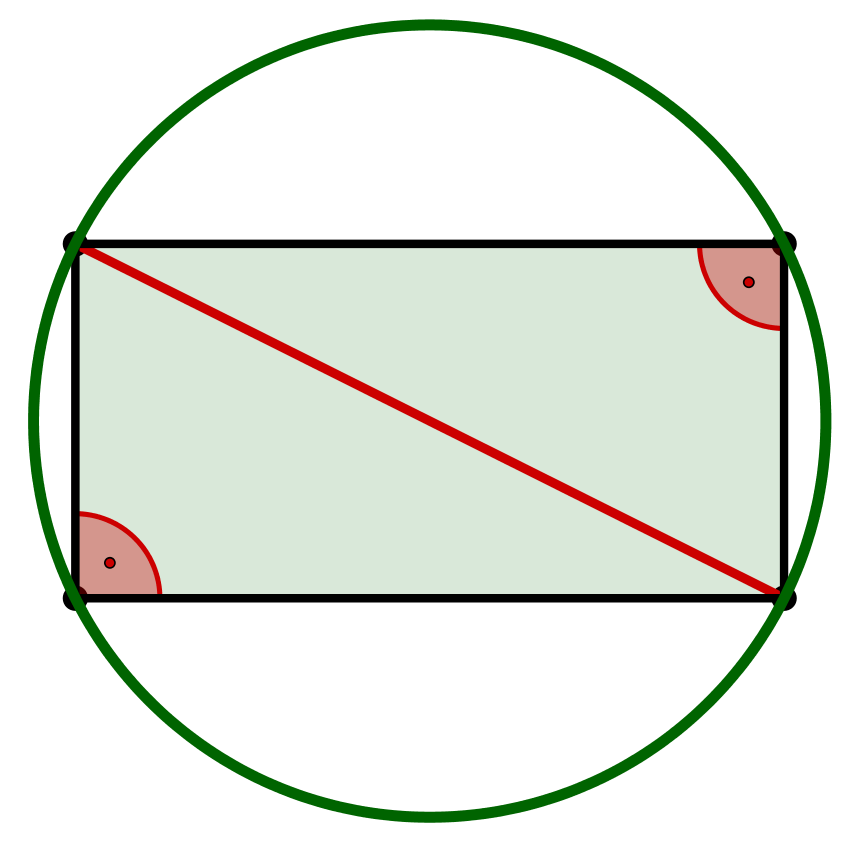 |  |
Goldenes Rechteck
Ein goldenes Rechteck ist ein Rechteck, bei dem die Seitenlängen im Verhältnis des goldenen Schnitts stehen:
Übungsaufgaben
Laden
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zu Rechtecken und Quadraten
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
