Aufgaben zur Flächeninhaltsberechung bei einem Kreis

1
Berechne den Flächeninhalt und Umfang eines Kreises mit dem
1. Radius $r = 1{,}5 \, cm$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Kreis
  Flächeninhalt
  $A = \pi \cdot r^2= \pi \cdot (1{,}5 \, cm)^2 = 3{,}14 \cdot 2{,}25\, cm^2 = 7{,}07 \, cm^2$
  Umfang
  $U=2 \cdot \pi \cdot r = 2 \cdot \pi \cdot 1{,}5 \, cm = 2 \cdot 3{,}14 \cdot 1{,}5 \, cm= 9{,}42 \, cm$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Radius $r= 4 \, cm$ .
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Kreis
  Flächeninhalt
  $A = \pi \cdot r^2= \pi \cdot (4 \, cm)^2 = 3{,}14 \cdot 16\, cm^2 = 50{,}24 \, cm^2$
  Umfang
  $U=2 \cdot \pi \cdot r = 2 \cdot \pi \cdot 4 \, cm = 2 \cdot 3{,}14 \cdot 4 \, cm= 25{,}12 \, cm$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2
Gib den Flächeninhalt eines Kreises mit dem Radius $2{,}5\,\text{cm}$ an.
Runde dein Ergebnis auf zwei Stellen nach dem Komma.
cm²

Für diese Aufgabe benötigst Du folgendes Grundwissen: Berechnungen am Kreis
$A = \pi \cdot r^2= \pi \cdot (2{,}5 \, cm)^2 = 3{,}14 \cdot 6{,}25\, cm^2 = 19{,}625 \, cm^2$
Runde auf 2 Stellen nach dem Komma.
$A\approx19{,}63\text{cm}^2$

Ermittle die fehlenden Größen in der Tabelle (auf die erste Dezimalstelle gerundet).

	a)	b)	c)	d)	e)
Radius r	1,5 cm	33,0 cm
Durchmesser d			2,4 m
Umfang U				71,6 m
Flächeninhalt					12,56 cm²

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kreisumfang und Kreisfläche

Berechnung der Kreisgrößen

Im Kreis gilt:

$\ U=2r\cdot\pi;\quad\ A=r^2\cdot\pi;\quad d=2r$

Berechnungen Spalte a.)

$\ d=2r\ \Rightarrow\ d=2\cdot1{,}5\ \text{cm}\$

$\ \boxed{d=3\ \text{cm}}$

$\ U=2r\cdot\pi\ \Rightarrow\ U=2\cdot1{,}5\ \text{cm}\cdot\pi$

$\ \boxed{U=9{,}4\ \text{cm}}$

$\ A=r^2\cdot\pi\ \Rightarrow\ A=2{,}25\ \text{cm}^2\cdot\pi$

$\ \boxed{A=7{,}1\ \text{cm}^2}$

Berechnungen Spalte b.) wie a.) jedoch $r=33{,}0\ \text{cm}$

Berechnungen Spalte c.)

$\ r=\dfrac{d}{2}\ \Rightarrow\ r=\dfrac{2{,}4\ \text{m}}{2}$

$\ \boxed{r=1{,}2\ \text{m}}$

$\ U=2r\cdot\pi\ \Rightarrow\ U=2\cdot1{,}2\ \text{m}\cdot\pi$

$\ \boxed{U=7{,}5\ \text{m}}$

$\ A=r^2\cdot\pi\ \Rightarrow\ A=1{,}44\ \text{cm}^2\cdot\pi$

$\ \boxed{A=4{,}5\ \text{m}^2}$

Berechnungen Spalte d.)

$\ U=2r\cdot\pi\ \Rightarrow\ 2r=\dfrac{U}{\pi}\ \Rightarrow\ 2r=\dfrac{71{,}6\text{\ m}}{\pi}$

$\ 2r=\boxed{d=22{,}8\text{\ m}}$

$\hspace{9mm}\boxed{r=11{,}4\text {\ m}}$

$\ A=r^2\cdot\pi\ \Rightarrow\ A=129{,}96\ \text{m}^2\cdot\pi$

$\ \boxed{A=408{,}3\text{\ m}^2}$

Berechnungen Spalte e.)

$\ A=r^2\cdot\pi\ \Rightarrow\ r=\sqrt{\dfrac{A}{\pi}}\ \Rightarrow\ r=\sqrt{\dfrac{12{,}6\text{\ cm}^2}{\pi}}$

$\ \boxed{r=2{,}0\ \text{cm}}\ \Rightarrow\ d=\ 2\cdot2{,}0\text{\ cm}$

$\ \boxed{d=4{,}0\text{\ cm}}$

$\ U=2r\cdot\pi\ \Rightarrow\ U=2\cdot2{,}0 \text{\ cm}\cdot\pi$

$\ \boxed{U=12{,}6\text{\ cm}}$

Ergänze die Tabelle entsprechend.

	a)	b)	c)	d)	e)
Radius r	1,5 cm	33,0 cm	1,2 m	11,4 m	2,0 cm
Durchmesser d	3,0 cm	66,0 cm	2,4 m	22,8 m	4,0 cm
Umfang U	9,4 cm	207,3 cm	7,5 m	71,6 m	12,6 cm
Flächeninhalt A	7,1 cm²	3421,2 cm²	4,5 m²	408,3 m²	12,6 cm²

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

4
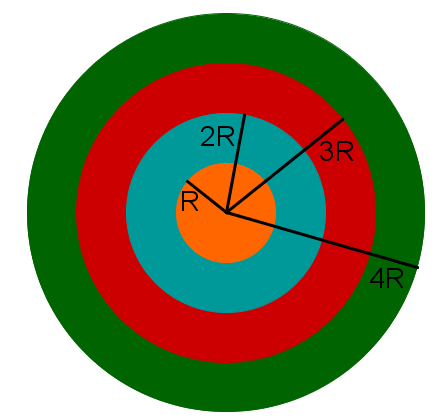
Begründe, wie sich jeweils Umfang und Flächeninhalt eines Kreises ändern, wenn man seinen Radius verdoppelt, verdreifacht bzw. vervierfacht.
Verdoppelt man den Radius, vervierfacht sich der Flächeninhalt.
Verdoppelt man den Radius, verdoppelt sich auch der Umfang.
Verdoppelt man den Radius, verdoppelt sich der Flächeninhalt.
Verdoppelt man den Radius, vervierfacht sich der Umfang.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Kreisumfang und Kreisfläche
Änderung des Umfangs beim Vervielfachen des Radius:
Stelle zuerst die Formel für den ursprünglichen, kleinen Umfang des Kreises auf.
$U_1=2\cdot r_1\cdot\pi$
Ebenfalls die Formel für den neuen Umfang aufstellen:
$U_2=2\cdot r_2\cdot\pi$
$r_1$ wird um den neuen Umfang $U_2$ zu erhalten vervielfacht: $r_2=n\cdot r_1$ . Setze ein.
$U_2=2\cdot\left(r_1\cdot n\right)\cdot\pi=n\cdot2\cdot r_1\cdot\pi$
Benutze $2\cdot r_1\cdot\pi=U_1$ um den Ausdruck zu vereinfachen.
$U_2=n\cdot U_1$
$\Rightarrow$ Das heißt der Umfang, des Kreises vergrößert sich um den Faktor $n$ .
Also wird der Umfang beispielsweise doppelt so groß, wenn der Radius verdoppelt wird.
Änderung des Flächeninhalts beim Vielfachen des Radius:
Stelle zuerst die Formel für den ursprünglichen Flächeninhalt des Kreises auf.
$A_1=r_1^2\pi$
Ebenfalls die Formel für den neuen Flächeninhalt aufstellen:
$A_2=r_2^2\pi$
$r_1$ wird um den neuen Flächeinhalt $A_2$ zu erhalten vervielfacht: $r_2=n\cdot r_1$
$A_2=\left(n\cdot r_1\right)^2\pi=n^2\cdot r_1^2\cdot\pi$
Benutze $r_1^2\pi=A_1$ , um den Zusammenhang zu vereinfachen.
$A_2=n^2\cdot{A}_1$
$\Rightarrow$ Multipliziert man den Radius $r$ mit $n$ , so wird der Flächeninhalt des Kreises immer mit $n^2$ vervielfacht. Zum Beispiel wird der Flächeninhalt bei Verdoppelung des Radius viermal so groß.

Berechne von den folgenden geometrischen Körpern/Figuren den Radius $r$ .

Ein Kreis hat den Umfang $U=6{,}283 \text{ cm}$ . Berechne den Radius $r$ . Runde das Ergebnis auf drei Dezimalstellen genau.

Ein Kreis hat die Fläche $A=7{,}35 \text{ m}^2$ . Berechne den Radius $r$ in $\text{cm}$ , runde dabei auf ganze $\text{cm}$ !

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle U$	$=$	$\displaystyle 2\pi r$	$\displaystyle :2\pi$
$\displaystyle \frac{U}{2\pi}$	$=$	$\displaystyle r$
	↓	Setze den Wert für den Umfang $U$ ein.
$\displaystyle r$	$=$	$\displaystyle \frac{6{,}283\text{ cm}}{2\pi}$
	↓	Berechne mit dem Taschenrechner und runde das Ergebnis.
$\displaystyle r$	$≈$	$\displaystyle 1{,}000\text{ cm}$

$\displaystyle A$	$=$	$\displaystyle \pi r^2$	$\displaystyle :\pi$
$\displaystyle \frac{A}{\pi}$	$=$	$\displaystyle r^2$
	↓	Ziehe die Wurzel.
$\displaystyle \pm\sqrt{\frac{A}{\pi}}$	$=$	$\displaystyle r$
	↓	Der Radius kann nur positiv sein. Daher kannst du das negtive Ergebnis ignorieren.
$\displaystyle r$	$=$	$\displaystyle \sqrt{\frac{A}{\pi}}$
	↓	Setze den Wert für die Fläche $A$ ein.
$\displaystyle r$	$=$	$\displaystyle \sqrt{\frac{7{,}35\text{ m}^2}{\pi}}$
	↓	Rechne mit dem Taschenrechner und runde das Ergebnis.
$\displaystyle r$	$≈$	$\displaystyle 1{,}53\text{ m}$
	↓	Rechne in $\text{cm}$ um.
$\displaystyle r$	$≈$	$\displaystyle 153\text{ cm}$

Aufgaben zur Flächeninhaltsberechung bei einem Kreis

Flächeninhalt

Umfang

Hast du eine Frage oder Feedback?

Flächeninhalt

Umfang

Hast du eine Frage oder Feedback?

Berechnung der Kreisgrößen

Ergänze die Tabelle entsprechend.

﻿

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?