Teil 1 Stochastik

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

Im Folgenden werden relative Häufigkeiten als Wahrscheinlichkeiten interpretiert.

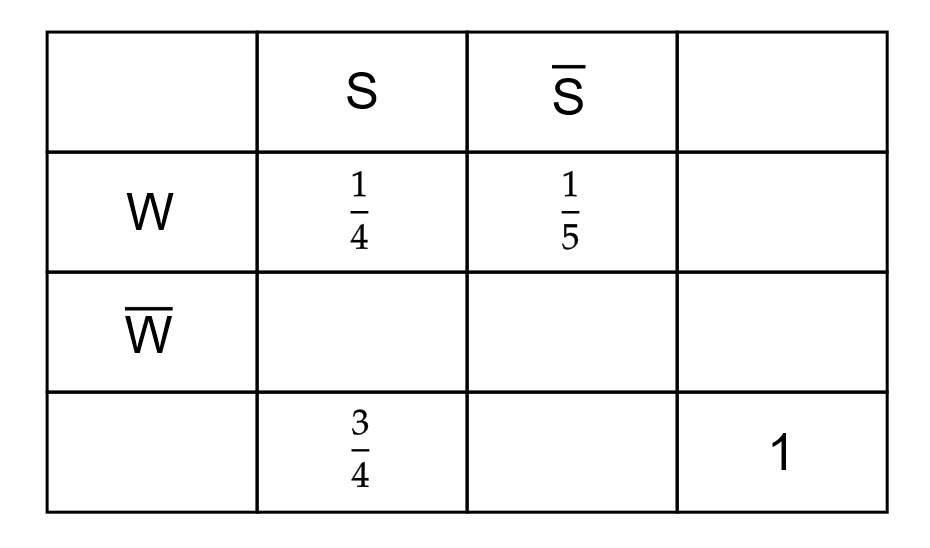
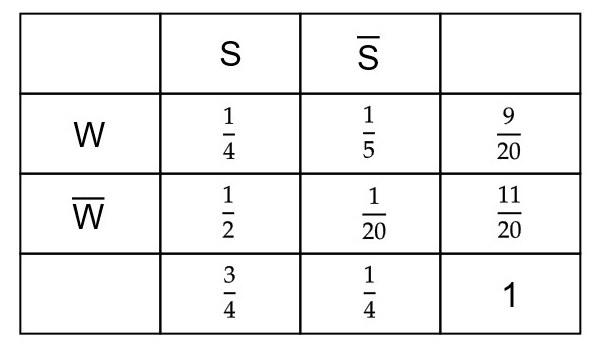
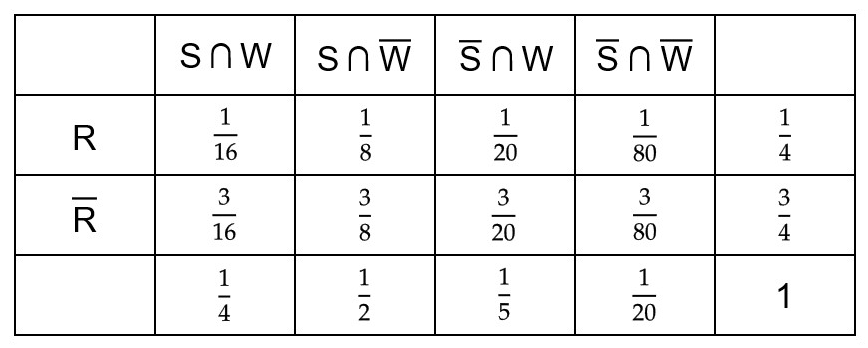
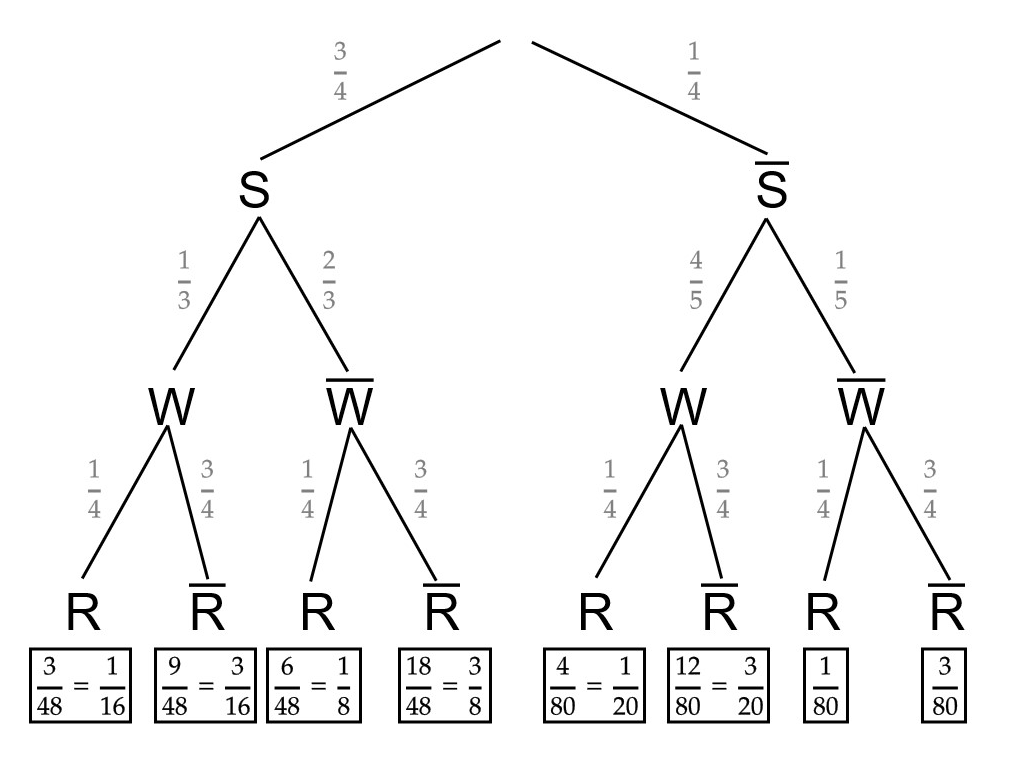
Eine Gemeinde in den Bergen ist ein beliebtes Reiseziel bei Winterurlaubern. Als Wintersportaktivitäten stehen Skifahren (S), Schneeschuhwandern (W) und Rodeln (R) zur Auswahl. Erfahrungsgemäß fahren drei Viertel der Urlauber Ski. Nur ein Drittel der Skifahrer nutzen auch das Angebot zum Schneeschuhwandern, unter den Nicht-Skifahrern unternehmen 80 % Schneeschuhwanderungen. Unabhängig von der Entscheidung für Skifahren oder Schneeschuhwandern geht jeder vierte Winterurlauber auch rodeln. Die Wahl der Wintersportaktivitäten eines beliebig herausgegriffenen Urlaubers wird als Zufallsexperiment aufgefasst. Geben Sie einen Term an, mit dem die Wahrscheinlichkeit berechnet werden kann, dass ein Urlauber genau zwei der Wintersportaktivitäten nachgeht. Zeichnen Sie dazu ein Baumdiagramm.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln

Berechnen der Wahrscheinlichkeiten der Ereignisse

Um die Werte der verschiedenen Wahrscheinlichkeiten zu berechnen, die man für das Baumdiagramm braucht, hilft es, Vierfeldertafeln zu erstellen.

Aus der Aufgabe kann man folgendes ablesen:

die Wahrscheinlichkeit, dass ein zufällig ausgewählter Urlauber skifährt ( $S$ ), beträgt $\frac{3}{4}$
die Wahrscheinlichkeit, dass ein Skifahrer auch schneeschuhwandert (( $S$ ) und ( $W$ )) , beträgt ein Drittel von $\frac{3}{4}$ , also $\frac{1}{4}$
die Wahrscheinlichkeit, dass ein Nicht-Skifahrer schneeschuhwandert (( $\overline{S}$ ) und ( $W$ ), beträgt 80 $\%$ von $\frac{1}{4}$ , also $\frac{1}{5}$

Jetzt kann man die leeren Felder durch ausrechnen füllen.

Danach erstellt man eine Vierfeldertafel für die aus der vorherigen Vierfeldertafel hervorgehenden Ereignisse $S\cap{W}$ , $S\cap{\overline{W}}$ , $\overline{S}\cap{W}$ und $\overline{S}\cap{\overline{W}}$ , geschnitten mit den Ergebnissen Rodeln (R) und

Nicht Rodeln ( $\overline{R}$ ):

Baumdiagramm erstellen

Aus diesen Ergebnissen kann man jetzt ein vollständiges Baumdiagramm erstellen:

Berechnen der Wahrscheinlichkeit, dass ein Urlauber genau zwei der Wintersportaktivitäten nachgeht

Um diese Wahrscheinlichkeit zu berechnen, addiert man jetzt einfach die Wahrscheinlichkeiten aller Pfade des Baumdiagramms, die auf die Beschreibung passen. Davon gibt es drei: den zweiten, den dritten und den fünften von links, also $S\cap W \cap \overline R$ $\left(\frac{3}{16}\right)$ , $S\cap\overline{W}\cap R$ $\left(\frac{1}{8}\right)$ und $\overline{S}\cap W\cap R$ $\left(\frac{1}{20}\right)$ .

	$\displaystyle \frac{3}{16}+\frac{1}{8}+\frac{1}{20}$
	↓ Erweitere, um die Brüche auf den selben Nenner zu bringen.
$=$	$\displaystyle \frac{15}{80}+\frac{10}{80}+\frac{4}{80}$
	↓ Addiere die Zähler und behalte den Nenner bei.
$=$	$\displaystyle \frac{29}{80}$
	↓ Rechne um in die Dezimalschreibweise.
$=$	$\displaystyle 0{,}3625$

Die Wahrscheinlichkeit, dass ein Urlauber genau zwei der Wintersportaktivitäten nachgeht, beträgt also $36{,}25 \%$ .

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Beim Kauf einer Liftkarte erhalten Personen, die Übernachtungsgäste in einem Hotel oder einer Pension vor Ort sind, einen Rabatt von 5 %. Erfahrungsgemäß ist dies bei 60 % aller Liftkartenkäufer der Fall. Kurz bevor der Lift in Betrieb geht, stehen an einer schon offenen Kasse bereits 15 Personen an. Interpretieren Sie folgenden Term im Sachzusammenhang:
$12\cdot 0{,}6^4\cdot 0{,}4^{11}$

Erfahrungsgemäß sind $60%$ % der Liftkartenkäufer Übernachtungsgäste. Damit ist die Wahrscheinlichkeit einen Übernachtungsgast anzutreffen genau $p=0{,}6$ und somit gilt für $q=0{,}4$ .
Vor der Kasse stehen 15 Personen und wegen der Wahrscheinlichkeiten $p$ und $q$ sind 4 Übernachtungsgäste und 11 Tagestouristen vor der Kasse. Wenn man sich die Liftkartenkäufer in einer Reihe vorstellt, so gibt es $\begin{pmatrix}15\\4\end{pmatrix}$ Möglichkeiten, die 4 Übernachtungsgäste auf die 15 Plätze zu verteilen.
Da $\begin{pmatrix}15\\4\end{pmatrix}>12$ gilt, sind die 4 Übernachtungsgäste nicht beliebig auf die 15 Plätze verteilt. Wenn aber die 4 Übernachtungsgäste benachbart sind, also die Plätze $1{,}2,3{,}4$ oder $2{,}3,4{,}5\lor 3{,}4,5{,}6\lor 4{,}5,6{,}7\lor...\lor12{,}13{,}14{,}15$ belegen, so gibt es genau $12$ Möglichkeiten.
Somit bedeutet: $12\cdot 0{,}6^4\cdot 0{,}4^{11}$ die Wahrscheinlichkeit für das Ereignis: Die $4$ Übernachtungsgäste stehen benachbart in der Reihe vor der offenen Kasse,
Zum Beispiel: HHHHTTTTTTTTTTT, THHHHTTTTTTTTTT, TTHHHHTTTTTTTTT,....
3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Um die Schneesicherheit zu erhöhen, wird im Skigebiet zwischen den Gemeinden Oberdorf ( $O$ ) und Unterdorf ( $\overline{O}$ ) darüber diskutiert, ob eine Beschneiungsanlage gebaut werden soll. Um sich einen Überblick zu verschaffen, wie die Einwohner zu diesem Vorhaben eingestellt sind, wird eine Umfrage durchgeführt. Aus den beiden Gemeinden nehmen insgesamt 1200 Personen daran teil. Die Auswertung ergab, dass unter den 700 befragten Oberdorfern 600 Befürworter ( $B$ ) sind. 25 % aller Befragten sind aus Unterdorf und äußern Einwände gegen die Anlage.
1. Bestimmen Sie mithilfe einer vollständigen Vierfeldertafel die Wahrscheinlichkeit, mit der ein zufällig ausgewählter Teilnehmer der Umfrage folgende Frage verneint: „Sind Sie aus Oberdorf und haben Sie gegen den Bau der Beschneiungsanlage gestimmt?“
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vierfeldertafel
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Es sind $700$ der Befragten aus Oberdorf (O). Somit sind $500$ der Befragten aus Unterdorf $(\overline{O}).$
  Weiter gilt $|B\cap O|=600\Rightarrow |\overline B\cap O|=100.$
  $25$ % aller Befragten sind aus Unterdorf und lehnen die Beschneiungsanlage ab. Also
  $|\overline B \cap \overline O|=\frac{1200}{4}=300$ .
  $\def\arraystretch{1.25} \begin{array}{c||c|c|c} \quad&O &\overline{O}\\\hline\hline B&600& \cdot&\cdot\\\hline \overline B &\cdot&300&\cdot\\\hline \cdot&700&500&1200 \end{array}$
  und ergänzt:
  $\def\arraystretch{1.25} \begin{array}{c||c|c|c} \quad&O &\overline{O}\\\hline\hline B&600& 200&800\\\hline \overline B &100&300&400\\\hline \cdot&700&500&1200 \end{array}$
  Damit ergibt sich für die Wahrscheinlichkeit des Ereignisses: "Sind Sie aus Oberdorf und haben Sie gegen die Beschneiungsanlage gestimmt" :
  $P(O\cap\overline B)=\frac{100}{1200}=\frac{1}{12}$ .
2. Geben Sie den Anteil der Befürworter der Beschneiungsanlage unter allen Befragten an und reflektieren Sie kritisch, ob die Umfrage für den Bau spricht.
  
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Aus der Vierfeldertafel in 3a) ergibt sich, dass $800$ aller Befragten für die Beschneiungsanlage gestimmt haben. Daher sind $\frac{2}{3}$ aller Befragten für den Bau der Anlage. Offensichtlich eine überwältigende Mehrheit.
  Da allerdings $300\$ der $500$ Befragten aus dem Unterdorf, also $60$ % der Befragten aus dem Unterdorf gegen die Beschneiungsanlage gestimmt haben, spricht die Umfrage nicht sicher für den Bau der Anlage.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?