In einem abgeschiedenen Dorf verbreitet der Bewohner Maxl zum Zeitpunkt das Gerücht, dass der berühmte Sänger Fritzi Vordergucker seinen Urlaub hier im Ort verbringen möchte.
Die Funktion beschreibt näherungsweise die Anzahl der Dorfbewohner, die nach Tagen von dem Gerücht gehört haben, und ist durch die Funktionsgleichung mit und festgelegt. Bei den Rechnungen kann auf die Verwendung von Einheiten verzichtet werden. Runden Sie Ihre Ergebnisse sinnvoll.
Ermitteln Sie die Parameter und , wenn nach 5 Tagen bereits 120 Dorfbewohner von dem Gerücht erfahren haben und am Anfang nur Maxl Bescheid wusste. (5 BE)
Berechnen Sie, nach wie vielen Tagen bereits 500 Bewohner von dem Gerücht gehört haben. (3 BE)
Bestimmen Sie und erklären Sie die Bedeutung dieses Grenzwertes im Sachzusammenhang. (2 BE)
Untersuchen Sie das Monotonieverhalten der Funktion .
Bestimmen Sie ferner das Verhalten der 1. Ableitungsfunktion von für und interpretieren Sie das Ergebnis im Sachzusammenhang. (5 BE)
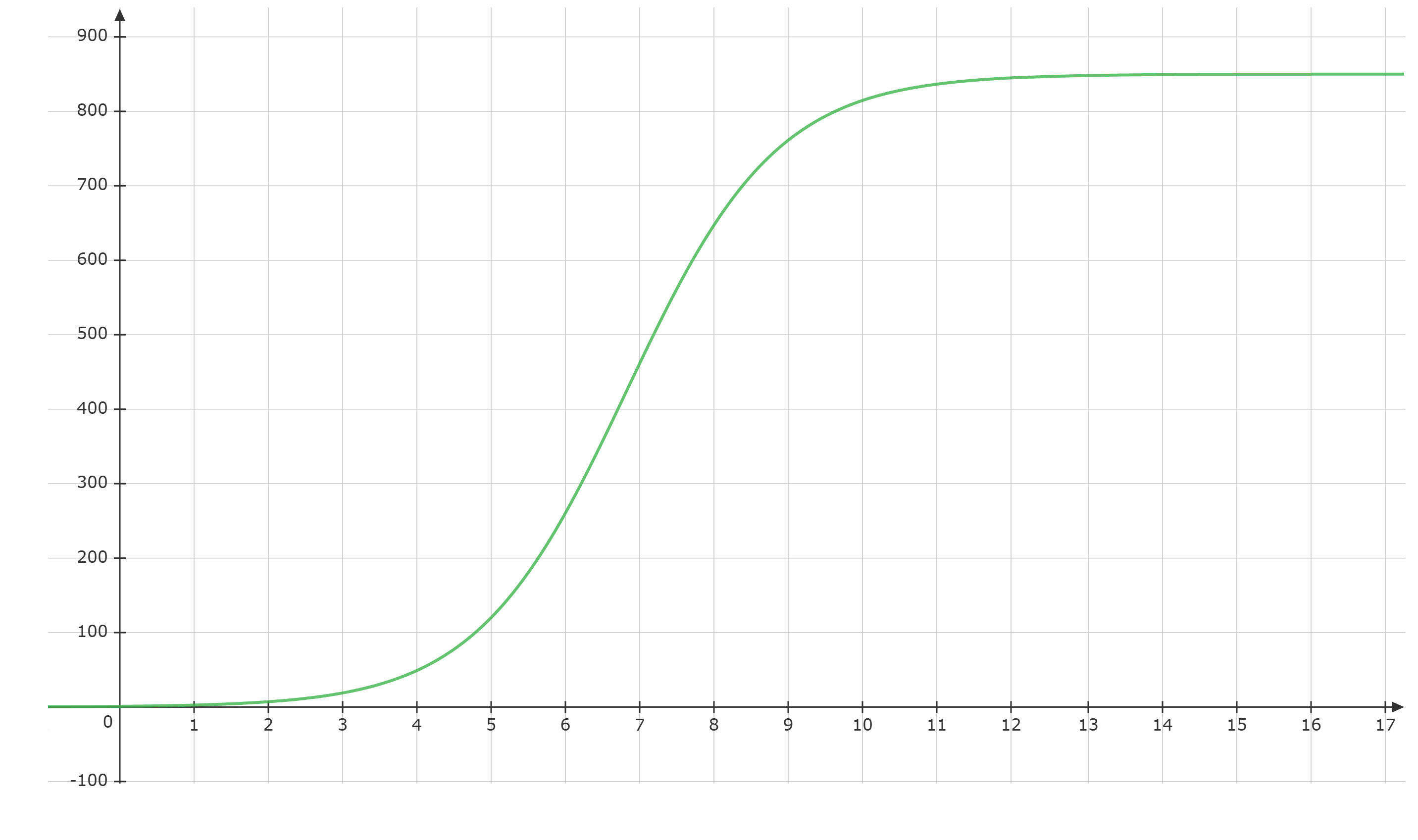
Zeichnen Sie für den Graphen von in ein geeignetes Koordinatensystem. (4 BE)