A I

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Gegeben ist die Funktion $f : \mapsto \frac{x^{2} - 4 x - 5}{2 x + 4}$ in der maximalen Definitionsmenge $D_{f} = ℝ$ . Ihr Graph heißt $G_{f}$ .
1. Bestimmen Sie die Nullstellen von $f$ und die Art der Definitionslücke. Ermitteln Sie das Verhalten der Funktionswerte in der Umgebung der Definitionslücke. (4 BE)
2. Ermitteln Sie die Gleichungen der beiden Asymptoten von $G_{f}$ und deren Art. (4 BE)
  $[T e i l e r g e b n i s : f (x) = \frac{1}{2} x - 3 + \frac{7}{2 x + 4}]$
3. Bestimmen Sie Art und Lage der Extrempunkte von $G_{f}$ . Geben Sie deren Koordinaten auf zwei Dezimalstellen gerundet an. (7 BE)
  $[M \ddot{o} g l i c h e s T e i l e r g e b n i s : f^{'} (x) = \frac{x^{2} + 4 x - 3}{2 (x + 2)^{2}}]$
4. Zeichnen Sie $G_{f}$ und seine Asymptoten unter Verwendung bisherigerErgebnisse für $- 8 \leq x \leq 8$ in ein kartesisches Koordinatensystem. (5 BE)
5. $G_{f}$ schließt mit der x-Achse ein endliches Flächenstück ein. Schraffieren Sie dieses in der Zeichnung von Teilaufgabe 1.4 und zeigen Sie, dass die exakte Maßzahl seines Flächeninhalts $12 - 3,5 \cdot l n (7)$ beträgt. (6 BE)
6. Bestimmen Sie die Gleichung der Tangente an $G_{f}$ bei $x = - 1$ , zeichnen Sie diese in das Koordinatensystem von Teilaufgabe 1.4 ein und berechnen Sieden Flächeninhalt des Dreiecks, das die Tangente mit der schiefen Asymptote von $G_{f}$ und der x-Achse einschließt. (6 BE)

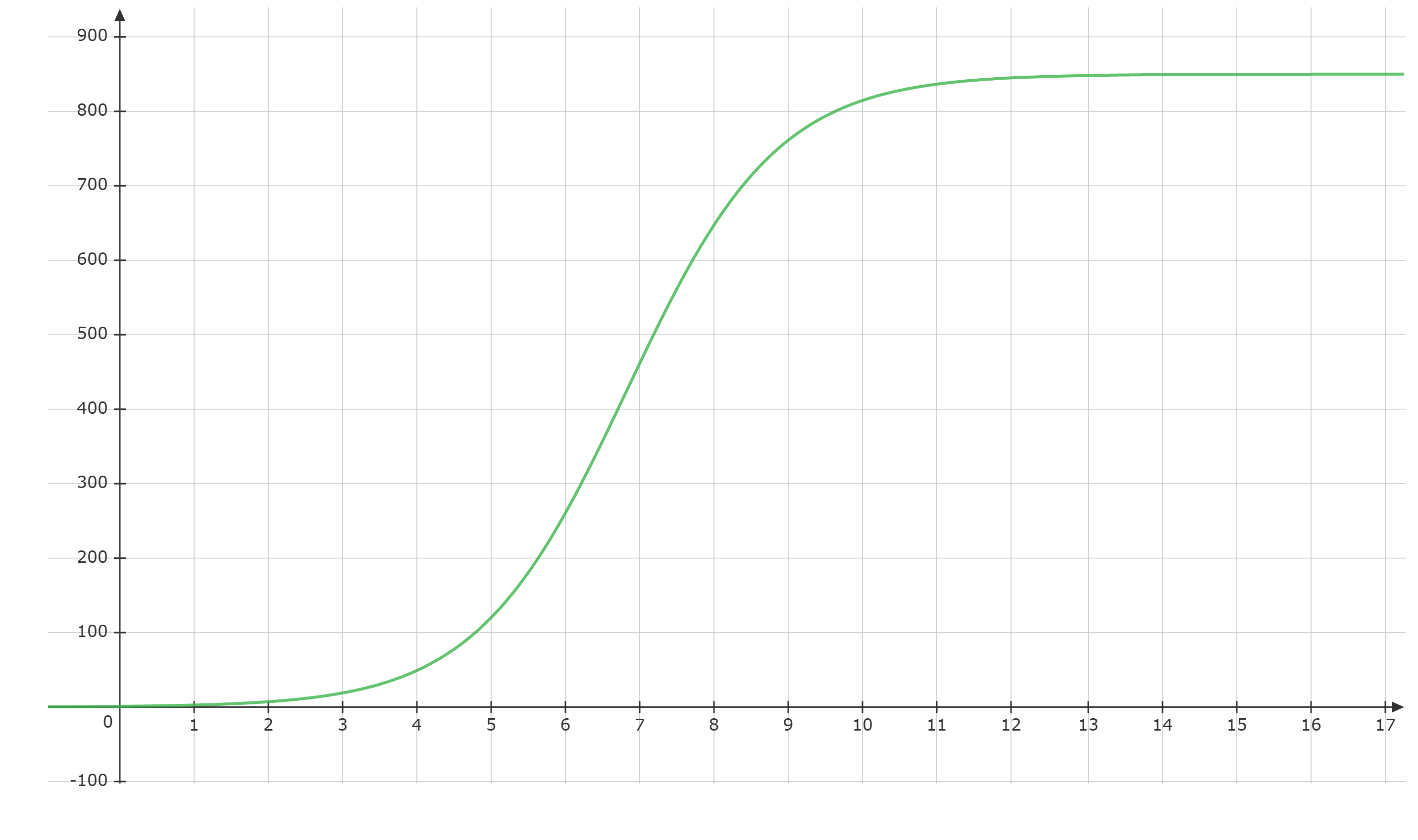
In einem abgeschiedenen Dorf verbreitet der Bewohner Maxl zum Zeitpunkt $t = 0$ das Gerücht, dass der berühmte Sänger Fritzi Vordergucker seinen Urlaub hier im Ort verbringen möchte.

Die Funktion $B$ beschreibt näherungsweise die Anzahl der Dorfbewohner, die nach $t$ Tagen von dem Gerücht gehört haben, und ist durch die Funktionsgleichung $B (t) = \frac{A}{1 + 849 \cdot e^{c \cdot t}}$ mit $t \geq 0$ und $A, c \in ℝ$ festgelegt. Bei den Rechnungen kann auf die Verwendung von Einheiten verzichtet werden. Runden Sie Ihre Ergebnisse sinnvoll.

Ermitteln Sie die Parameter $A$ und $c$ , wenn nach 5 Tagen bereits 120 Dorfbewohner von dem Gerücht erfahren haben und am Anfang nur Maxl Bescheid wusste. (5 BE)

$[Ergebnis : A = 850; c = 0,988]$

Berechnen Sie, nach wie vielen Tagen bereits 500 Bewohner von dem Gerücht gehört haben. (3 BE)

Bestimmen Sie $\lim_{t \to \infty} B (t)$ und erklären Sie die Bedeutung dieses Grenzwertes im Sachzusammenhang. (2 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Überblick – Limes-Schreibweise
Bestimmung des Limes
Wenn man für $t$ sehr große Zahlen einsetzt, dann wird der Exponent von $e$ eine sehr große negative Zahl. $e$ strebt dann gegen $0$ und der Nenner strebt gegen $1$ . Also strebt der gesamt Bruch gegen 850, wenn $t$ gegen $\infty$ strebt:
$\lim_{t \to \infty} \frac{850}{1 + 849 \cdot e^{- 0,988 \cdot t}} = 850$
Erklärung des Wertes im Sachzusammenhang
Das Gerücht kann sich nicht auf mehr als $850$ Bewohner ausbreiten. Daraus kann man ableiten, dass in dem Dorf insgesamt $850$ Leute wohnen.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Überlege, welchen Wert der Funktionsterm annimmt, wenn man für $t$ sehr große Zahlen einsetzt
Erkläre dann, was das Ergebnis über Maxls Dorf aussagt

Untersuchen Sie das Monotonieverhalten der Funktion $B$ .

Bestimmen Sie ferner das Verhalten der 1. Ableitungsfunktion von $B$ für $t \to + \infty$ und interpretieren Sie das Ergebnis im Sachzusammenhang. (5 BE)

$[Teilergebnis : \dot{B} (t) = \frac{712 990,2 \cdot e^{- 0,988 t}}{(1 + 849 \cdot e^{- 0,988 t})^{2}}]$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Monotonieverhalten berechnen

Ableitung der Funktion bestimmen

	$(\frac{850}{1 + 849 \cdot e^{- 0,988 \cdot t}})^{'}$
	↓ Wende die Quotientenregel an
$=$	$\frac{0 \cdot (1 + 849 \cdot e^{- 0,988 \cdot t}) - 850 \cdot (849 \cdot e^{- 0,988 \cdot t}) \cdot (- 0,988)}{(1 + 849 \cdot e^{- 0,988 \cdot t})^{2}}$
$=$	$\frac{0 - (- 712 990,2 \cdot e^{- 0,988 \cdot t})}{(1 + 849 \cdot e^{- 0,988 \cdot t})^{2}}$
$=$	$\frac{712 990,2 \cdot e^{- 0,988 \cdot t}}{(1 + 849 \cdot e^{- 0,988 \cdot t})^{2}}$

Extremwerte berechnen

Setze die Ableitung gleich null:
	↓
$0$	$=$	$\frac{712 990,2 \cdot e^{- 0,988 \cdot t}}{(1 + 849 \cdot e^{- 0,988 \cdot t})^{2}}$	$\cdot (1 + 849 \cdot e^{- 0,988 \cdot t})^{2}$
$0$	$=$	$712 990,2 \cdot e^{- 0,988 \cdot t}$	$/ 712 990,2$
$0$	$=$	$e^{- 0,988 \cdot t}$

Da $e^{x}$ niemals $0$ werden kann, hat die Ableitung keine Nullstelle, das heißt, der Graph von $f (x)$ hat keinen Extrempunkt.

Steigung der Funktion bestimmen

Da der Graph von $f (x)$ keine Extremstellen hat, ist er entweder streng monoton steigend oder fallend. Um das herauszufinden, schaut man sich die Ableitung an:

\frac{712 990,2 \cdot e^{- 0,988 \cdot t}}{(1 + 849 \cdot e^{- 0,988 \cdot t})^{2}}

Dabei fällt auf das weder der Zähler noch der Nenner einen negativen Wert annehmen können:

Da $e^{- 0.988 \cdot t}$ , egal für welches t nur positive Werte ergibt und $712 990,2$ eine positive Zahl ist, ist der Zähler immer positiv
Da der Term im Nenner quadriert wird, ist der Nenner immer positiv

Der ganze Bruch kann also auch nur positive Werte annehmen.

$\Rightarrow$ Die Ableitung ist nie negativ, dass heißt, der Graph der Funktion $f (x)$ steigt

streng monoton.

Verhalten der Ableitungsfunktion im Unendlichen bestimmen

Für diese Aufgabe benötigst Du folgendes Grundwissen: Überblick - Limes-Schreibweise

Wenn $t$ gegen $+ \infty$ strebt, streben beide $e^{- 0,988}$ gegen $0$ , sowohl im Nenner als auch im Zähler. Der Zähler als Ganzes strebt somit ebenfalls gegen $0$ . Im Nenner strebt das Produkt aus $849$ und $e^{- 0,988}$ gegen $0$ , was bedeutet, dass der ganze Nenner gegen $1$ strebt. Insgesamt strebt also der Zähler gegen $0$ und der Nenner gegen $1$ . Somit strebt der ganze Bruch gegen $0$ .

\lim_{t \to + \infty} \frac{712 990,2 \cdot e^{- 0,988 \cdot t}}{(1 + 849 \cdot e^{- 0,988 \cdot t})^{2}} = 0

Erklärung im Sachzusammenhang

Strebt $t$ gegen unendlich, strebt die Ableitung also gegen $0$ . Im Sachzusammenhang bedeutet das, wenn mehr Zeit vergeht, sinkt die Zahl derer, die von dem Gerücht erfahren, irgendwann auf $0$ , weil alle Bewohner schon davon gehört haben.

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Zeichnen Sie für $t \in [0; 16]$ den Graphen von $B$ in ein geeignetes Koordinatensystem. (4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Graph einer Funktion
Wertetabelle erstellen
Setze verschiedene Werte in die Funktion ein, runde gegebenenfalls und erstelle eine Wertetabelle:
0
1
2
3
4
5
6
7
8
$1$
$2,7$
$7,2$
$19$
$49,1$
$120,2$
$260,6$
$461,4$
$647,1$
9
10
11
12
13
14
15
16
$761,2$
$814,6$
$836,5$
$844,9$
$848,1$
$849,3$
$849,7$
$849,9$
Wähle nun ein geeignetes Koordinatensystem, trage die Werte ein und verbinde die Punkte zu einem Graphen:
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Erstelle mithilfe der Funktion eine Wertetabelle
Trage die Werte in ein geeignetes Koordinatensystem ein
Verbinde die Punkte

3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Zur Wiederaufforstung von steilen Gebirgshängen werden zunächst Baumsetzlinge gezüchtet und anschließend gepflanzt. Die Höhe $h$ (in $c m$ ) eines Baumsetzlings in Abhängigkeit von der Zeit $t$ (in Monaten) wird durch folgende Funktion $h$ näherungsweise beschrieben:
$h : t \mapsto 70 + 30 \cdot \ln (3 t + 2)$ für $t \in [0; 240]$ .
Die Pflanzung des Setzlings erfolgt zum Zeitpunkt $t = 0$ . Nach $240$ Monaten ist das Höhenwachstum im Wesentlichen beendet. Auf die Verwendung von Einheiten kann bei der Rechnung verzichtet werden. Ergebnisse sind sinnvoll zu runden.
1. Berechnen Sie die Höhe eines Setzlings zum Zeitpunkt der Anpflanzung und am Ende der Wachstumsphase. (2 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung der Logarithmus-Funktion
  Die Funktion $h : t \mapsto 70 + 30 \cdot \ln (3 t + 2)$ beschreibt die Höhe des Setzlings in Abhängigkeit der Zeit $t$ beschreibt. Um die Aufgabe zu lösen, setze die Werte $0$ und $240$ ein und rechne aus:
  $h (0) = 70 + 30 \cdot \ln (3 \cdot 0 + 2) \approx 90,8$
  $h (240) = 70 + 30 \cdot \ln (3 \cdot 240 + 2) \approx 267,5$
  Der Setzling hatte bei der Pflanzung eine Höhe von $90,8 c m$ und am Ende der Wachstumsperiode $267,5 c m$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Haben die Bäume eine Höhe von mindestens $250 c m$ erreicht, sind sie sicher mit dem Gebirgshang verwurzelt und können so einen Murenabgang nach sehr starken Regenfällen verhindern.
  Berechnen Sie, wie viele Jahre es ab dem Beginn der Pflanzung dauert, bis ein Murenabgang aufgrund der Aufforstung erfolgreich abgewendet werden kann. (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung der Logarithmus-Funktion
  Suche den Zeitpunkt $t$ , zu dem die Bäume die Höhe von $250 c m$ genau erreichen. Setze dafür die Funktion $h$ gleich $250$ und löse nach $t$ auf:
  $h (t) = 250$
  $70 + 30 \cdot \ln (3 t + 2) = 250$
  $\Leftrightarrow 30 \cdot \ln (3 t + 2) = 180$
  $\Leftrightarrow \ln (3 t + 2) = 6$
  $\Leftrightarrow 3 t + 2 = e^{6}$
  $\Leftrightarrow t = \frac{e^{6} - 2}{3} \approx 133,8$
  Dabei wurde im vorletzten Schritt beide Seiten exponiert. Auf der linken Seite kürzt sich dann wegen $e^{\ln (3 t + 2)} = 3 t + 2$ der Logarithmus raus.
  Damit müssen mehr als 134 Monate vergehen, bis die Bäume Murenabgänge verhindern können. Das sind ungefähr $\frac{134}{12} \approx 11,2$ Jahre. Das heißt, es müssen mindestens 12 Jahre vergehen, bis die Bäume stark genug verwurzelt sind.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Zeigen Sie, dass die Baumsetzlinge für $t = 0$ am stärksten wachsen. (4 BE) $[Teilergebnis: \dot{h} (t) = \frac{90}{3 t + 2}]$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung der Logarithmus-Funktion
  Die Funktion $h$ beschreibt die Höhe der Setzlinge. Wenn du die Funktion $h$ ableitest, dann beschreibt das die Änderung der Höhe, damit also die Wachstumsrate. Berechne also die Ableitung von $h$ :
  $h^{'} (t) = (70)^{'} + 30 \cdot (\ln (3 t + 2))^{'} = 30 \cdot (\ln (3 t + 2))^{'}$
  Die Summe lässt sich getrennt ableiten, der erste Summand fällt als Konstante weg. Um den zweiten Summand abzuleiten, benötigst du die Kettenregel. Dabei ist die innere Funktion $3 t + 2$ , ihre Ableitung ist 3 (Stichwort Nachdifferenzieren). Damit gilt
  $(\ln (3 t + 2))^{'} = \frac{1}{3 t + 2} \cdot 3 = \frac{3}{3 t + 2}$
  Insgesamt gilt also
  $h^{'} (t) = 30 \cdot \frac{3}{3 t + 2} = \frac{90}{3 t + 2}$
  Nun suchst du die höchste Wachstumsrate und damit das Maximum von $h^{'}$ .
  Du siehst, dass $h^{'}$ eine Hyperbel ist, die ihre Polstelle bei $t = - \frac{2}{3}$ hat. Als monoton fallende Funktion im Bereich $t > - \frac{2}{3}$ muss also die Stelle 0 das Maximum im Intervall $[0,240]$ sein.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

0	1	2	3	4	5	6	7	8
$1$	$2,7$	$7,2$	$19$	$49,1$	$120,2$	$260,6$	$461,4$	$647,1$

9	10	11	12	13	14	15	16
$761,2$	$814,6$	$836,5$	$844,9$	$848,1$	$849,3$	$849,7$	$849,9$

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$120$	$=$	$\frac{850}{1 + 849 \cdot e^{5 c}}$	$\cdot (1 + 849 \cdot e^{5 c})$
$120 \cdot (1 + 849 \cdot e^{5 c})$	$=$	$850$
$120 + 101 880 \cdot e^{5 c}$	$=$	$850$	$- 120$
$101 880 \cdot e^{5 c}$	$=$	$730$	$/ 101.880$
$e^{5 c}$	$=$	$\frac{73}{10.188}$	$l n$
$5 c$	$=$	$\ln (\frac{73}{10.188})$	$/ 5$
$c$	$=$	$\frac{\ln (\frac{73}{10.188})}{5}$
	↓	Berechne und runde
$c$	$\approx$	$- 0,988$

$500$	$=$	$\frac{850}{1 + 849 \cdot e^{- 0,988 \cdot t}}$	$\cdot (1 + 849 \cdot e^{- 0,988 \cdot t})$
$500 \cdot (1 + 849 \cdot e^{- 0,988 \cdot t})$	$=$	$850$
$500 + 424 500 \cdot e^{- 0,988 \cdot t}$	$=$	$850$	$- 500$
$424 500 \cdot e^{- 0,988 \cdot t}$	$=$	$350$	$/ 424.500$
$e^{- 0,988 \cdot t}$	$=$	$\frac{350}{424 500}$
$e^{- 0,988 \cdot t}$	$=$	$\frac{7}{8.490}$	$\ln$
$- 0,988 \cdot t$	$=$	$\ln (\frac{7}{8 490})$	$/ (- 0,988)$
$t$	$=$	$\frac{\ln (\frac{7}{8 490})}{- 0,988}$
	↓	Berechne und runde
$t$	$\approx$	$7,2$

A I

Gleichungen aufstellen

Gleichungen umformen

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Bestimmung des Limes

Erklärung des Wertes im Sachzusammenhang

Hast du eine Frage oder Feedback?

Ableitung der Funktion bestimmen

Extremwerte berechnen

Steigung der Funktion bestimmen

Verhalten der Ableitungsfunktion im Unendlichen bestimmen

Erklärung im Sachzusammenhang

Hast du eine Frage oder Feedback?

Wertetabelle erstellen

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?