Analysis, Teil A, Aufgabengruppe 2
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
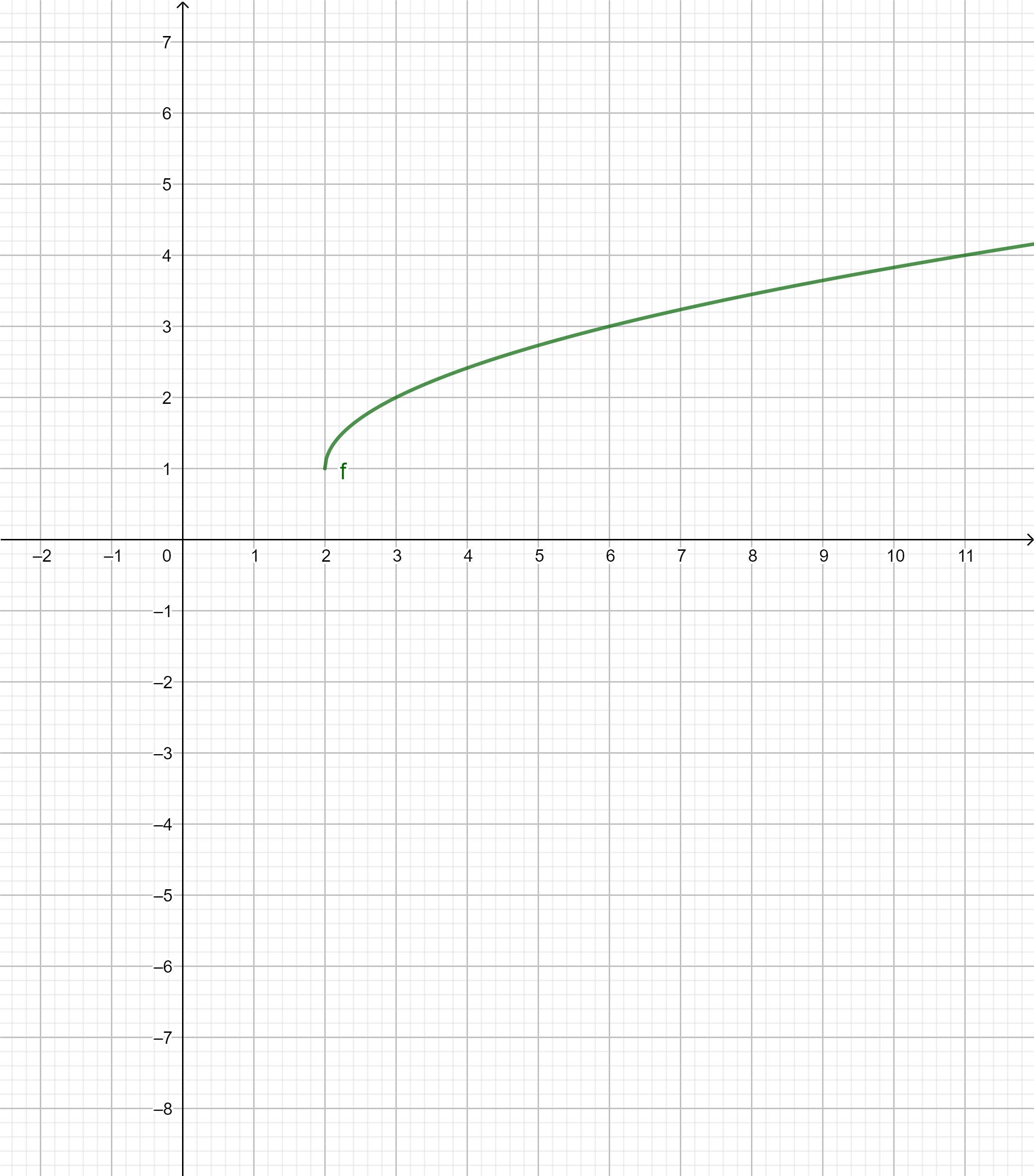
Gegeben ist die Funktion mit und maximalem Definitionsbereich.
Zeichnen Sie den Graphen von im Bereich in ein Koordinatensystem. (3P)
Berechnen Sie den Wert des Integrals . (3P)
- 2
Geben Sie jeweils den Term einer in definierten Funktion an, die die angegebene Wertemenge hat.
(2P)
(2P)
- 3
Wir betrachten im Folgenden zwei verschiedene Funktionen.
Betrachtet werden eine in definierte ganzrationale Funktion und der Punkt . Beschreiben Sie, wie man rechnerisch die Gleichung der Tangente an den Graphen von p im Punkt Q ermitteln kann. (2P)
Gegeben ist eine in definierte Funktion mit , deren Graph im Punkt die Tangente mit der Gleichung besitzt. Bestimmen Sie und . (3P)
- 4
Die Abbildung zeigt den Graphen einer in definierten Funktion . ist streng monoton fallend und schneidet die x-Achse im Punkt . Betrachtet wird ferner die Funktion mit und maximalem Definitionsbereich .
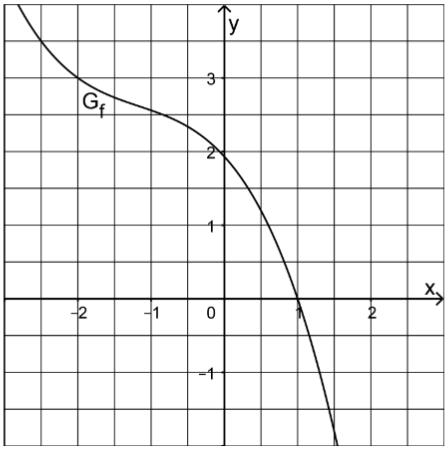
Begründen Sie, dass nicht in enthalten ist, und geben Sie den Funktionswert an. (2P)
Ermitteln Sie mithilfe der Abbildung die x-Koordinaten der Schnittpunkte der Graphen von und . (3P)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?