Teil A
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
Aufgabe A1
Informationen über die Leistungsfähigkeit eines Sportlers kann man mithilfe von sogenannten Laktat-Tests ermitteln, da die Laktat-Konzentration im Blut mit steigender Laufgeschwindigkeit zunimmt.
Bei einem solchen Test wird die Laktat-Konzentration (Millimol pro Liter Blut) in Abhängigkeit von der Geschwindigkeit erfasst.
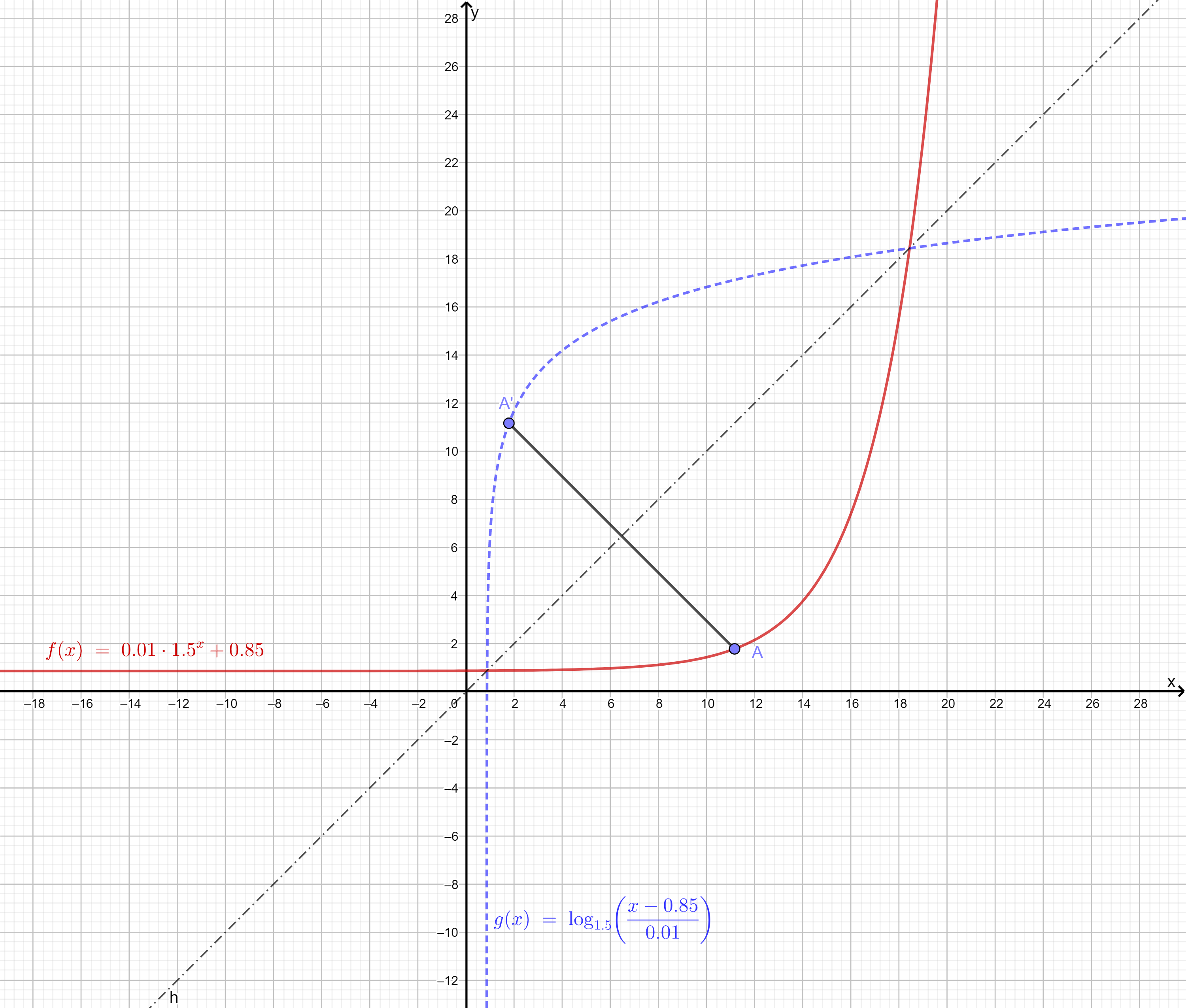
Für Paul lässt sich dieser Zusammenhang bei einem Test näherungsweise durch die Funktion mit der Gleichung () beschreiben.
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
Bei Paul wurde für die Geschwindigkeiten von und jeweils eine Messung der Laktat-Konzentration durchgeführt.
Berechnen Sie mithilfe der Funktion die zugehörigen Funktionswerte für diese beiden Geschwindigkeiten und ermitteln Sie sodann, um wie viel Prozent sich die Laktat-Konzentration zwischen diesen beiden Messungen erhöht hat. (3 P)
Berechnen Sie die nach aufgelöste Gleichung der Umkehrfunktion zu . (2 P)
- 2
Aufgabe A2
Punkte und Punkte liegen auf der Geraden mit der Gleichung
(). Sie sind für zusammen mit dem Punkt und Punkten Eckpunkte von Trapezen .
Es gilt: [] [].
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
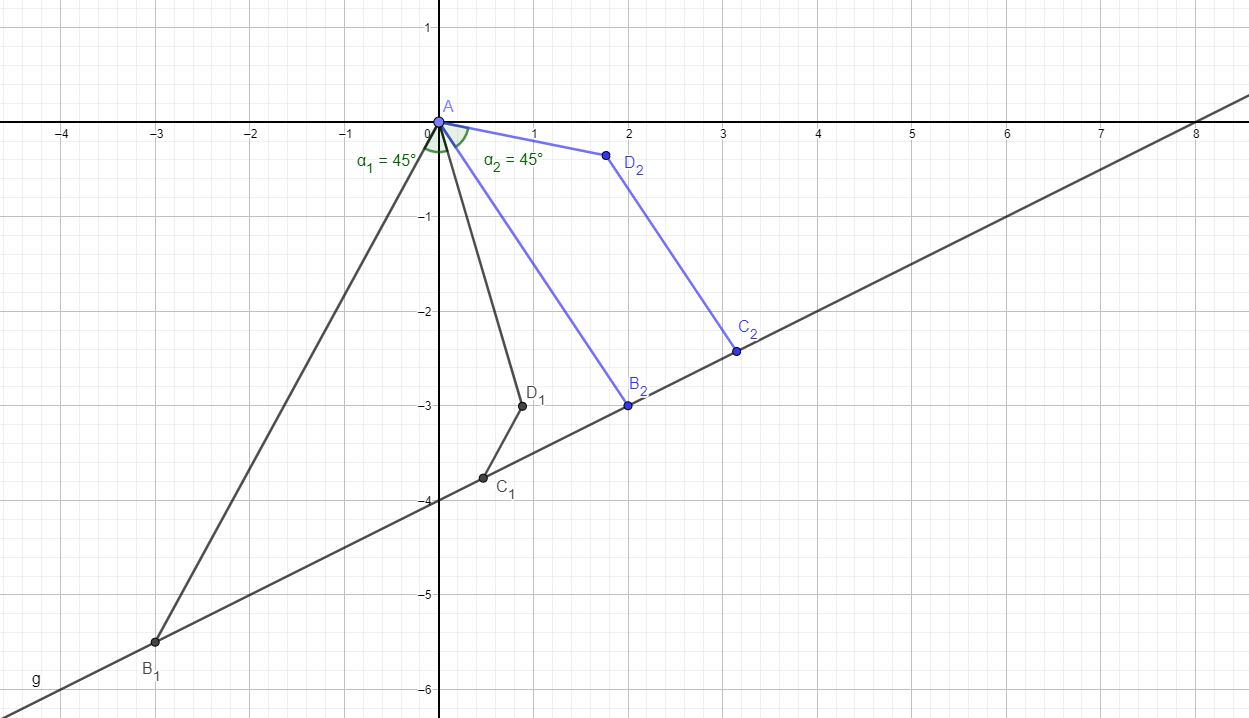
Im Koordinatensystem sind die Gerade und das Trapez für bereits eingezeichnet.
Zeichnen Sie das Trapez für ein. (1 P)
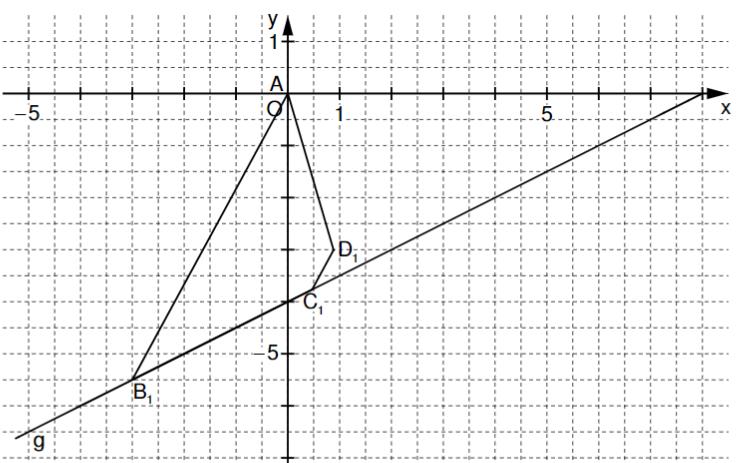
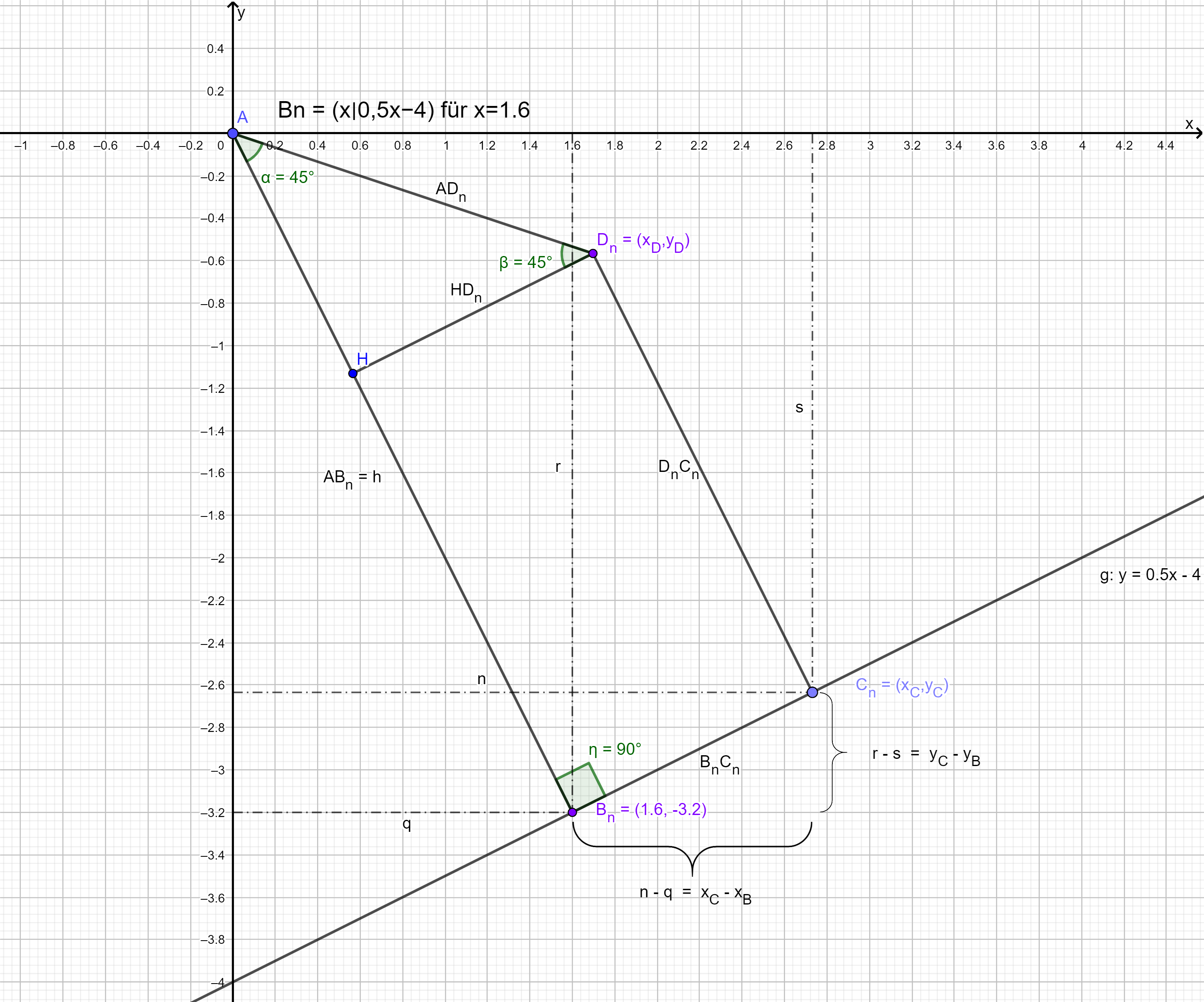
Im Trapez gilt: .
Berechnen Sie den zugehörigen Wert von . (3 P)
Zeigen Sie rechnerisch, dass für die Koordinaten der Punkte in Abhängigkeit von gilt: . (3 P)
Berechnen Sie die Gleichung des Trägergraphen der Punkte und zeichnen Sie diesen in das Koordinatensystem zu 2a) ein. (3 P)
- 3
Aufgabe A3
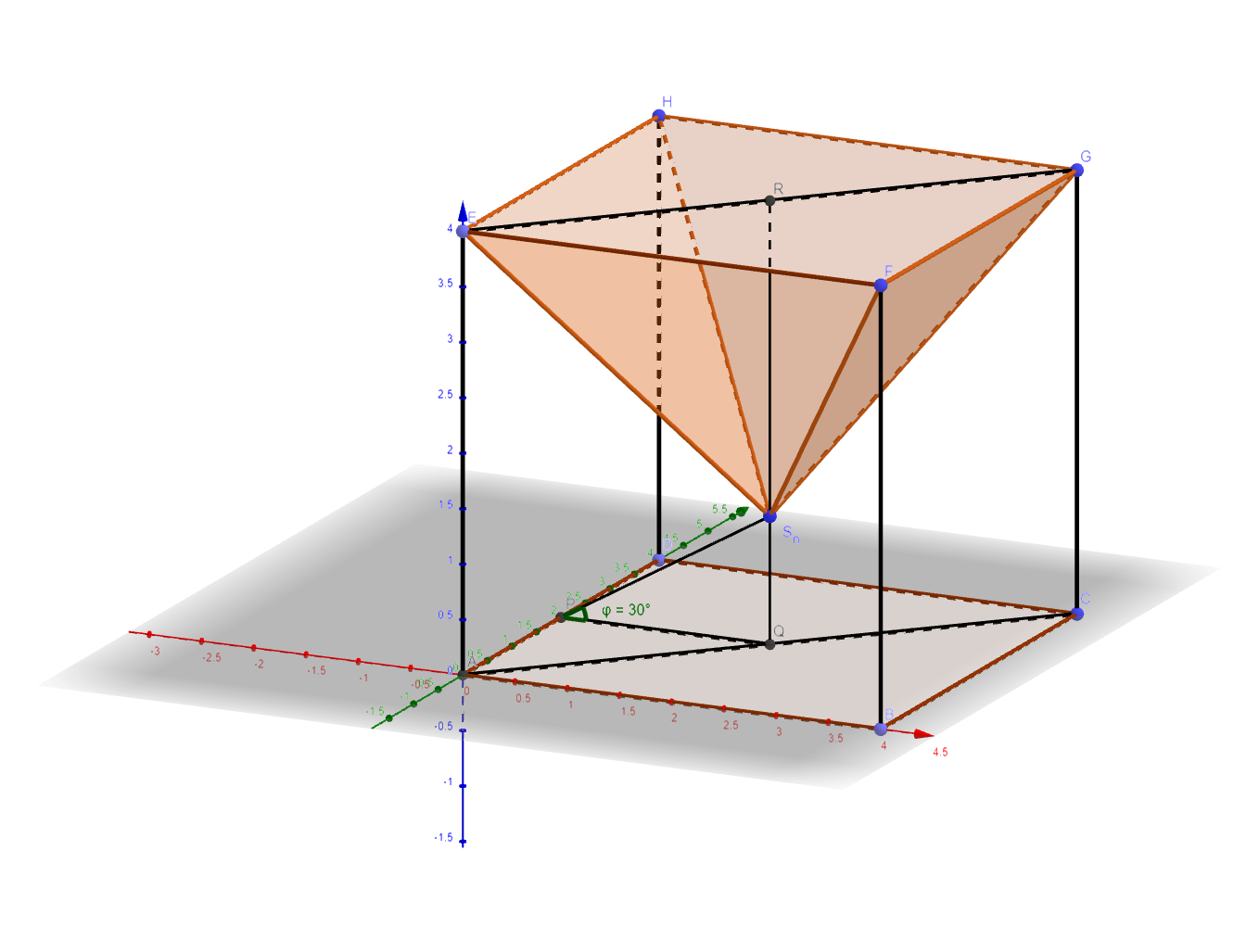
Gegeben ist ein Schrägbild des Würfels mit .
ist der Mittelpunkt der Strecke , ist der Mittelpunkt der Strecke und ist der Mittelpunkt der Strecke .
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
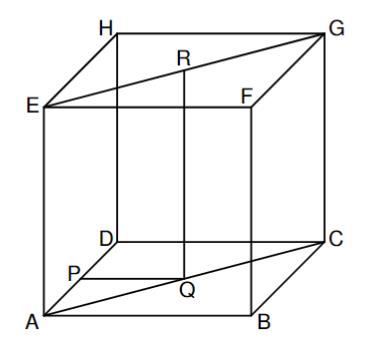
Punkte legen zusammen mit und Winkel mit dem Maß fest.
Sie sind für die Spitzen von Pyramiden mit der Grundfläche .
Zeichnen Sie die Strecke und die Pyramide für in die Zeichnung zu 3 ein. (1 P)
Zeigen Sie rechnerisch, dass für das Volumen der Pyramiden in Abhängigkeit von gilt: . (3 P)
Unter den Pyramiden hat die Pyramide das maximale Volumen .
Begründen Sie, weshalb gilt: (2 P)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?