Spiegelung einer Geraden an einer Geraden

Der Artikel beschreibt die Spiegelung einer Geraden $g$ an einer Geraden $h$ .

Es werden zwei verschiedene Berechnungsmöglichkeiten vorgestellt.

1. Berechnung mit dem Lotfußpunkt $F$

2 Berechnung mit einer Hilfsebene $H$

Berechnungsmöglichkeit 1 mit Lotfußpunkt $F$

Gegeben sind zwei Geraden $g : \vec{x} = \vec{O A} + r \cdot \vec{u}$ und $h : \vec{x} = \vec{O B} + s \cdot \vec{v}$ .

Die Gerade $g$ wird an der Geraden $h$ gespiegelt.

Vorgehensweise

1. Ermittle je nach Lagebeziehung zwischen den beiden Geraden entweder von einem Punkt auf der Geraden $g$ oder von 2 Punkten auf der Geraden $g$ die Koordinaten der Punkte $P$ und $Q$ . Spiegele dann den Punkt $P$ an der Geraden $h$ und gegebenenfalls auch den Punkt $Q$ .

2. Schreibe einen allgemeinen Vektor für einen Punkt $F_{1}$ auf der Geraden $h$ :

$\vec{O F_{1}} = (\begin{array}{c} b_{1} + s \cdot v_{1} \\ b_{2} + s \cdot v_{2} \\ b_{3} + s \cdot v_{3} \end{array})$

3. Bilde den Vektor $\vec{P F_{1}} = \vec{O F_{1}} - \vec{O P}$ .

4. Der Vektor $\vec{P F_{1}}$ muss senkrecht auf der Geraden $h$ stehen, d.h. das Skalarprodukt ist gleich null: $\vec{P F_{1}} \circ \vec{v} = 0$ . Diese Gleichung liefert für den Parameter $s$ einen Wert $s_{F}$ .

5. Setze $s_{F}$ in $\vec{O F_{1}}$ ein und berechne den Spiegelpunkt mithilfe der Gleichung:

$\vec{O P^{'}} = \vec{O P} + 2 \cdot \vec{P F_{1}}$ oder $\vec{O P^{'}} = \vec{O F_{1}} + \vec{P F_{1}}$

6. Verfahre gegebenenfalls für den zweiten Punkt $Q$ entsprechend und berechne den Spiegelpunkt $Q^{'}$ .

Beispiel zu Berechnungsmöglichkeit 1

Gegeben sind die beiden (echt) parallelen Geraden $g : \vec{x} = (\begin{array}{c} 1 \\ 1 \\ 2 \end{array}) + r \cdot (\begin{array}{c} 2 \\ 2 \\ 2 \end{array})$ und $h : \vec{x} = (\begin{array}{c} 3 \\ 2 \\ 1 \end{array}) + s \cdot (\begin{array}{c} 2 \\ 2 \\ 2 \end{array})$ . Die Gerade $g$ wird an der Geraden $h$ gespiegelt.

1. Benutze den Aufpunkt der Geraden $g$ : $P (1 | 1 | 2)$ .

(Da die beiden Geraden parallel zueinander sind, genügt es diesen Punkt zu spiegeln.)

Spiegele den Punkt $P$ an der Geraden $h$ .

2. Schreibe einen allgemeinen Vektor für einen Punkt $F$ auf der Geraden $h$ :

$\vec{O F} = (\begin{array}{c} 3 + 2 s \\ 2 + 2 s \\ 1 + 2 s \end{array})$

3. Bilde den Vektor $\vec{P F} = \vec{O F} - \vec{O P}$ .

$\vec{P F} = (\begin{array}{c} 3 + 2 s \\ 2 + 2 s \\ 1 + 2 s \end{array}) - (\begin{array}{c} 1 \\ 1 \\ 2 \end{array}) = (\begin{array}{c} 2 + 2 s \\ 1 + 2 s \\ - 1 + 2 s \end{array})$ .

4. Berechne das Skalarprodukt: $\vec{P F} \circ \vec{v} = 0$ .

$(\begin{array}{c} 2 + 2 s \\ 1 + 2 s \\ - 1 + 2 s \end{array}) \circ (\begin{array}{c} 2 \\ 2 \\ 2 \end{array}) = 0$

$(2 + 2 s) \cdot 2 + (1 + 2 s) \cdot 2 + (- 1 + 2 s) \cdot 2$	$=$	$0$
	↓	Löse die Klammern auf.
$4 + 4 s + 2 + 4 s - 2 + 4 s$	$=$	$0$
	↓	Fasse zusammen.
$4 + 12 s$	$=$	$0$	$- 4$
$12 s$	$=$	$- 4$	$: 12$
$s$	$=$	$- \frac{4}{12}$
	↓	Kürze.
$s$	$=$	$- \frac{1}{3}$

5. Setze $s = - \frac{1}{3}$ in $\vec{P F}$ ein:

$\vec{P F} = (\begin{array}{c} 2 + 2 \cdot (- \frac{1}{3}) \\ 1 + 2 \cdot (- \frac{1}{3}) \\ - 1 + 2 \cdot (- \frac{1}{3}) \end{array}) = (\begin{array}{c} \frac{4}{3} \\ \frac{1}{3} \\ - \frac{5}{3} \end{array})$

Berechne den Spiegelpunkt mithilfe der Gleichung: $\vec{O P^{'}} = \vec{O P} + 2 \cdot \vec{P F}$

$\vec{O P^{'}} = (\begin{array}{c} 1 \\ 1 \\ 2 \end{array}) + 2 \cdot (\begin{array}{c} \frac{4}{3} \\ \frac{1}{3} \\ - \frac{5}{3} \end{array}) = (\begin{array}{c} 1 + \frac{8}{3} \\ 1 + \frac{2}{3} \\ 2 - \frac{10}{3} \end{array}) = (\begin{array}{c} \frac{11}{3} \\ \frac{5}{3} \\ - \frac{4}{3} \end{array})$

Der Spiegelpunkt $P^{'}$ hat die Koordinaten: $P^{'} (\frac{11}{3} | \frac{5}{3} | - \frac{4}{3})$ .

6. Der berechnete Spiegelpunkt ist der Aufpunkt der Spiegelgeraden $g^{'}$ . Für den Richtungsvektor der Spiegelgeraden nimmt man den Richtungsvektor $\vec{u} = (\begin{array}{c} 1 \\ 1 \\ 2 \end{array})$ der Geraden $g$ . Somit ergibt sich für die Gleichung der Spiegelgeraden:

$g^{'} : \vec{x} = \vec{O P^{'}} + t \cdot \vec{u}$ $\Rightarrow g^{'} : \vec{x} = (\begin{array}{c} \frac{11}{3} \\ \frac{5}{3} \\ - \frac{4}{3} \end{array}) + t \cdot (\begin{array}{c} 2 \\ 2 \\ 2 \end{array})$

Berechnung für sich schneidende Geraden und windschiefe Geraden

1. Im Fall sich schneidender Geraden $g$ und $h$ muss ein beliebiger Punkt $P$ der Geraden $g$ an der Geraden $h$ gespiegelt werden. Der gespiegelte Punkt $P^{'}$ und der Schnittpunkt $S$ , der bei der Spiegelung erhalten bleibt, sind zwei Punkte, die auf der gespiegelten Geraden $g^{'}$ liegen. Mit diesen beiden Punkten kann die Geradengleichung erstellt werden:

g^{'} : \vec{x} = \vec{O P^{'}} + t \cdot (\vec{O S} - \vec{O P^{'}})

2. Im Fall windschiefer Geraden $g$ und $h$ müssen jeweils zwei Punkte $P$ und $Q$ der Geraden $g$ ermittelt und an der Geraden $h$ gespiegelt werden. Mit diesen beiden Spiegelpunkten $P^{'}$ und $Q^{'}$ kann die Geradengleichung $g^{'}$ erstellt werden:

g^{'} : \vec{x} = \vec{O P^{'}} + t \cdot (\vec{O Q^{'}} - \vec{O P^{'}})

Berechnungsmöglichkeit 2 mit einer Hilfsebene H

Hier werden zwei Fälle unterschieden:

Fall 1: Die beiden Geraden sind (echt) parallel zueinander

Fall 2: Die beiden Geraden schneiden sich in einem Punkt $S$ .

(Der Fall windschiefer Geraden wird als Sonderfall in einem Spoiler am Artikelende behandelt.)

1. Fall:

Gegeben sind zwei (echt) parallele Geraden $g : \vec{x} = \vec{O P} + r \cdot \vec{u}$ und $h : \vec{x} = \vec{O Q} + s \cdot \vec{u}$ .

Die Gerade $g$ wird an der Geraden $h$ gespiegelt.

Vorgehensweise

Berechnung der gespiegelten Geraden g' mit einer Hilfsebene $H$

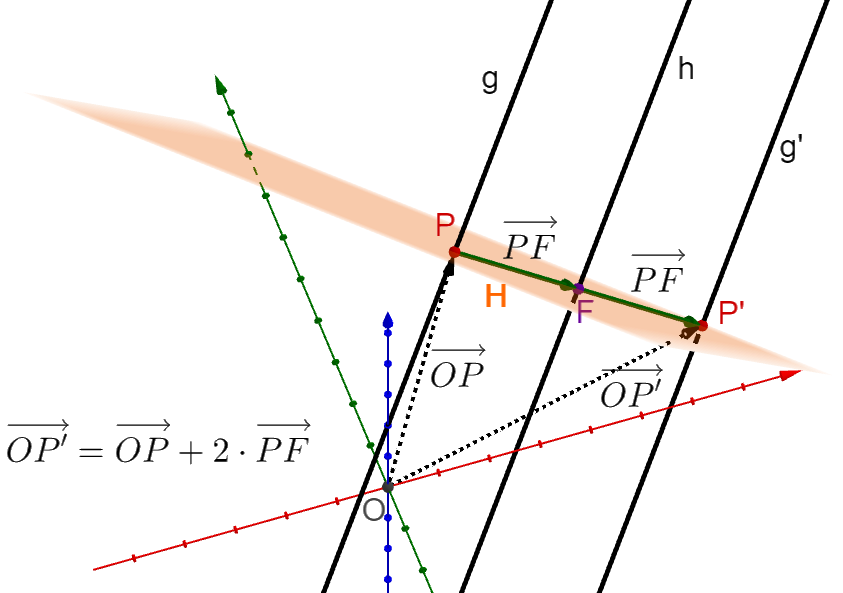
1. Erstelle eine Hilfsebene $H$ in Normalenform $E : (\vec{x} - \vec{O A}) \circ \vec{n} = 0$

Verwende dabei für $H$ den Aufpunkt $P$ der Geraden $g$ und setze für den Normalenvektor $\vec{n}$ den Richtungsvektor $\vec{u}$ der Geraden $g$ ein.

$H : (\vec{x} - \vec{O P}) \circ \vec{u} = 0$

2. Schneide die Gerade $h$ mit der Hilfsebene $H$ . Du erhältst den Fußpunkt $F$ .

3. Berechne den Vektor $\vec{P F}$

4. Zur Berechnung des Spiegelpunktes $P^{'}$ setze $\vec{O P}$ und $\vec{P F}$ in die Vektorgleichung $\vec{O P^{'}} = \vec{O P} + 2 \cdot \vec{P F}$ ein.

5. Der berechnete Punkt $P^{'}$ ist der Aufpunkt der Spiegelgeraden g'. Die Spiegelgerade hat den Richtungsvektor $\vec{u}$ (parallele Gerade zu $g$ und $h$ ) $\Rightarrow g^{'} : \vec{x} = \vec{O P^{'}} + t \cdot \vec{u}$

Beispiel zu Fall 1

1. Erstelle die Gleichung einer Hilfsebene $H$ mit dem Aufpunkt $P$ der Geraden $g$ und dem Richtungsvektor $\vec{u}$ der Geraden $g$ als Normalenvektor:

$H : (\vec{x} - (\begin{array}{c} 1 \\ 1 \\ 2 \end{array})) \circ (\begin{array}{c} 2 \\ 2 \\ 2 \end{array}) = 0$

2. Schneide $h$ mit $H$ :

$(\vec{x} - (\begin{array}{c} 1 \\ 1 \\ 2 \end{array})) \circ (\begin{array}{c} 2 \\ 2 \\ 2 \end{array})$	$=$	$0$
	↓	Setze $h : \vec{x} = (\begin{array}{c} 3 \\ 2 \\ 1 \end{array}) + s \cdot (\begin{array}{c} 2 \\ 2 \\ 2 \end{array})$ in $H$ ein.
$((\begin{array}{c} 3 \\ 2 \\ 1 \end{array}) + s \cdot (\begin{array}{c} 2 \\ 2 \\ 2 \end{array}) - (\begin{array}{c} 1 \\ 1 \\ 2 \end{array})) \circ (\begin{array}{c} 2 \\ 2 \\ 2 \end{array})$	$=$	$0$
	↓	Berechne die Vektordifferenz in der Klammer.
$((\begin{array}{c} 2 \\ 1 \\ - 1 \end{array}) + s \cdot (\begin{array}{c} 2 \\ 2 \\ 2 \end{array})) \circ (\begin{array}{c} 2 \\ 2 \\ 2 \end{array})$	$=$	$0$
	↓	Fasse zusammen.
$(\begin{array}{c} 2 + 2 s \\ 1 + 2 s \\ - 1 + 2 s \end{array}) \circ (\begin{array}{c} 2 \\ 2 \\ 2 \end{array})$	$=$	$0$
	↓	Berechne das Skalarprodukt.
$(2 + 2 s) \cdot 2 + (1 + 2 s) \cdot 2 + (- 1 + 2 s) \cdot 2$	$=$	$0$
	↓	Löse die Klammern auf.
$4 + 4 s + 2 + 4 s - 2 + 4 s$	$=$	$0$
	↓	Löse nach $s$ auf.
$12 s + 4$	$=$	$0$	$- 4$
$12 s$	$=$	$- 4$	$: 12$
$s$	$=$	$- \frac{4}{12}$
	↓	Kürze
$s$	$=$	$- \frac{1}{3}$

Setze $s = - \frac{1}{3}$ in die Geradengleichung $h$ ein, um den Punkt $F$ zu berechnen.

${\vec{x}}_{F} = (\begin{array}{c} 3 \\ 2 \\ 1 \end{array}) + (- \frac{1}{3}) \cdot (\begin{array}{c} 2 \\ 2 \\ 2 \end{array}) = (\begin{array}{c} 3 - \frac{2}{3} \\ 2 - \frac{2}{3} \\ 1 - \frac{2}{3} \end{array}) = (\begin{array}{c} \frac{7}{3} \\ \frac{4}{3} \\ \frac{1}{3} \end{array}) \Rightarrow$ $F (\frac{7}{3} | \frac{4}{3} | \frac{1}{3})$

3. Berechne den Vektor $\vec{P F}$

$\vec{P F} = \vec{O F} - \vec{O P} = (\begin{array}{c} \frac{7}{3} \\ \frac{4}{3} \\ \frac{1}{3} \end{array}) - (\begin{array}{c} 1 \\ 1 \\ 2 \end{array}) = (\begin{array}{c} \frac{4}{3} \\ \frac{1}{3} \\ - \frac{5}{3} \end{array})$

4. Setze $\vec{O P}$ und $\vec{P F}$ in die Vektorgleichung $\vec{O P^{'}} = \vec{O P} + 2 \cdot \vec{P F}$ ein:

Der Spiegelpunkt hat die Koordinaten $P^{'} (\frac{11}{3} | \frac{5}{3} | - \frac{4}{3})$ .

5. Setze in $g^{'} : \vec{x} = \vec{O P^{'}} + t \cdot \vec{u}$ den Spiegelpunkt $P^{'}$ und den Richtungsvektor $\vec{u}$ der Geraden $g$ ein.

Antwort: Die Gleichung der Spiegelgeraden lautet: $g^{'} : \vec{x} = (\begin{array}{c} \frac{11}{3} \\ \frac{5}{3} \\ - \frac{4}{3} \end{array}) + t \cdot (\begin{array}{c} 2 \\ 2 \\ 2 \end{array})$

Anmerkung: Die obige Darstellung zeigt das berechnete Beispiel im 1. Fall.

2. Fall:

Gegeben sind zwei sich im Punkt $S$ schneidende Geraden $g : \vec{x} = \vec{O P} + r \cdot \vec{u}$ und $h : \vec{x} = \vec{O Q} + s \cdot \vec{v}$ . Die Gerade $g$ wird an der Geraden $h$ gespiegelt.

Vorgehensweise

Berechnung der gespiegelten Geraden g' mit einer Hilfsebene $H$

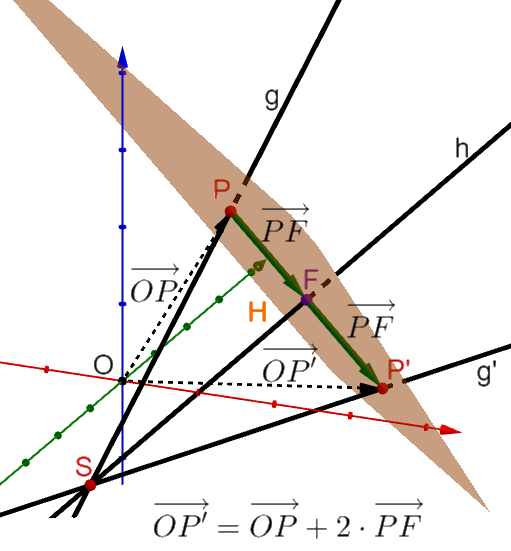
Spiegelung von zwei sich schneidenden Geraden

1. Erstelle eine Hilfsebene $H$ in Normalenform $E : (\vec{x} - \vec{O A}) \circ \vec{n} = 0$

Verwende dabei für $H$ den Aufpunkt $P$ der Geraden $g$ und setze für den Normalenvektor $\vec{n}$ den Richtungsvektor $\vec{v}$ der Geraden $h$ ein.

$H : (\vec{x} - \vec{O P}) \circ \vec{v} = 0$

2. Schneide die Gerade $h$ mit der Hilfsebene $H$ . Du erhältst den Fußpunkt $F$ .

3. Berechne den Vektor $\vec{P F}$

4. Zur Berechnung des Spiegelpunktes $P^{'}$ setze $\vec{O P}$ und $\vec{P F}$ in die Vektorgleichung $\vec{O P^{'}} = \vec{O P} + 2 \cdot \vec{P F}$ ein.

5. Der berechnete Punkt $P^{'}$ ist der Aufpunkt der Spiegelgeraden $g^{'}$ . Die Spiegelgerade hat den Richtungsvektor $\vec{P^{'} S}$ (mit dem gegebenen Geradenschnittpunkt $S$ ):

$\Rightarrow g^{'} : \vec{x} = \vec{O P^{'}} + t \cdot \vec{P^{'} S}$

Beispiel zu Fall 2

Gegeben sind die Gerade $g : \vec{x} = (\begin{array}{c} 1 \\ 1 \\ 2 \end{array}) + r \cdot (\begin{array}{c} 1 \\ 2 \\ 3 \end{array})$ , die Gerade $h : \vec{x} = (\begin{array}{c} 3 \\ 2 \\ 2 \end{array}) + s \cdot (\begin{array}{c} 2 \\ 2 \\ 2 \end{array})$ und der Schnittpunkt der beiden Geraden $S (0 | - 1 | - 1)$ .

1. Erstelle die Gleichung einer Hilfsebene $H$ mit dem Aufpunkt $P$ der Geraden $g$ und dem Richtungsvektor $\vec{v}$ der Geraden $h$ als Normalenvektor:

$H : (\vec{x} - (\begin{array}{c} 1 \\ 1 \\ 2 \end{array})) \circ (\begin{array}{c} 2 \\ 2 \\ 2 \end{array}) = 0$

2. Schneide $h$ mit $H$ :

$(\vec{x} - (\begin{array}{c} 1 \\ 1 \\ 2 \end{array})) \circ (\begin{array}{c} 2 \\ 2 \\ 2 \end{array})$	$=$	$0$
	↓	Setze $h : \vec{x} = (\begin{array}{c} 3 \\ 2 \\ 2 \end{array}) + s \cdot (\begin{array}{c} 2 \\ 2 \\ 2 \end{array})$ in $H$ ein.
$((\begin{array}{c} 3 \\ 2 \\ 2 \end{array}) + s \cdot (\begin{array}{c} 2 \\ 2 \\ 2 \end{array}) - (\begin{array}{c} 1 \\ 1 \\ 2 \end{array})) \circ (\begin{array}{c} 2 \\ 2 \\ 2 \end{array})$	$=$	$0$
	↓	Berechne die Vektordifferenz in der Klammer.
$((\begin{array}{c} 2 \\ 1 \\ 0 \end{array}) + s \cdot (\begin{array}{c} 2 \\ 2 \\ 2 \end{array})) \circ (\begin{array}{c} 2 \\ 2 \\ 2 \end{array})$	$=$	$0$
	↓	Fasse zusammen.
$(\begin{array}{c} 2 + 2 s \\ 1 + 2 s \\ 0 + 2 s \end{array}) \circ (\begin{array}{c} 2 \\ 2 \\ 2 \end{array})$	$=$	$0$
	↓	Berechne das Skalarprodukt.
$(2 + 2 s) \cdot 2 + (1 + 2 s) \cdot 2 + (0 + 2 s) \cdot 2$	$=$	$0$
	↓	Löse die Klammern auf.
$4 + 4 s + 2 + 4 s + 4 s$	$=$	$0$
	↓	Löse nach $s$ auf.
$12 s + 6$	$=$	$0$	$- 6$
$12 s$	$=$	$- 6$	$: 12$
$s$	$=$	$- \frac{6}{12}$
	↓	Kürze
$s$	$=$	$- \frac{1}{2}$

Setze $s = - \frac{1}{2}$ in die Geradengleichung $h$ ein, um den Punkt $F$ zu berechnen.

${\vec{x}}_{F} = (\begin{array}{c} 3 \\ 2 \\ 2 \end{array}) + (- \frac{1}{2}) \cdot (\begin{array}{c} 2 \\ 2 \\ 2 \end{array}) = (\begin{array}{c} 3 - \frac{2}{2} \\ 2 - \frac{2}{2} \\ 2 - \frac{2}{2} \end{array}) = (\begin{array}{c} 2 \\ 1 \\ 1 \end{array}) \Rightarrow$ $F (2 | 1 | 1)$

3. Berechne den Vektor $\vec{P F}$

$\vec{P F} = \vec{O F} - \vec{O P} = (\begin{array}{c} 2 \\ 1 \\ 1 \end{array}) - (\begin{array}{c} 1 \\ 1 \\ 2 \end{array}) = (\begin{array}{c} 1 \\ 0 \\ - 1 \end{array})$

4. Setze $\vec{O P}$ und $\vec{P F}$ in die Vektorgleichung $\vec{O P^{'}} = \vec{O P} + 2 \cdot \vec{P F}$ ein:

$\vec{O P^{'}} = (\begin{array}{c} 1 \\ 1 \\ 2 \end{array}) + 2 \cdot (\begin{array}{c} 1 \\ 0 \\ - 1 \end{array}) = (\begin{array}{c} 1 + 2 \\ 1 + 0 \\ 2 - 2 \end{array}) = (\begin{array}{c} 3 \\ 1 \\ 0 \end{array})$

Der Spiegelpunkt hat die Koordinaten $P^{'} (3 | 1 | 0)$ .

5. Berechne den Vektor $\vec{P^{'} S} = \vec{O S} - \vec{O P^{'}} = (\begin{array}{c} 0 \\ - 1 \\ - 1 \end{array}) - (\begin{array}{c} 3 \\ 1 \\ 0 \end{array}) = (\begin{array}{c} - 3 \\ - 2 \\ - 1 \end{array})$

Der berechnete Punkt $P^{'}$ ist der Aufpunkt der Spiegelgeraden $g^{'}$ . Die Spiegelgerade hat den Richtungsvektor $\vec{P^{'} S}$ (mit dem gegebenen Geradenschnittpunkt $S$ ):

$\Rightarrow g^{'} : \vec{x} = \vec{O P^{'}} + t \cdot \vec{P^{'} S}$

Setze in $g^{'}$ den Spiegelpunkt $P^{'}$ und den Richtungsvektor $\vec{P^{'} S}$ ein.

Antwort: Die Gleichung der Spiegelgeraden lautet $g^{'} : \vec{x} = (\begin{array}{c} 3 \\ 1 \\ 0 \end{array}) + t \cdot (\begin{array}{c} - 3 \\ - 2 \\ - 1 \end{array})$ bzw.

$g^{'} : \vec{x} = (\begin{array}{c} 3 \\ 1 \\ 0 \end{array}) + t \cdot (\begin{array}{c} 3 \\ 2 \\ 1 \end{array})$ .

Anmerkung: Die obige Darstellung zeigt das berechnete Beispiel im 2. Fall.

Übungsaufgaben

Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zur Spiegelung in der analytischen Geometrie

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Spiegelung einer Geraden an einer Geraden

Berechnungsmöglichkeit 1 mit Lotfußpunkt F

Vorgehensweise

Beispiel zu Berechnungsmöglichkeit 1

Berechnung für sich schneidende Geraden und windschiefe Geraden

Berechnungsmöglichkeit 2 mit einer Hilfsebene H

1. Fall:

Vorgehensweise

Berechnung der gespiegelten Geraden g' mit einer Hilfsebene H

Beispiel zu Fall 1

2. Fall:

Vorgehensweise

Berechnung der gespiegelten Geraden g' mit einer Hilfsebene H

Beispiel zu Fall 2

Übungsaufgaben

Berechnungsmöglichkeit 1 mit Lotfußpunkt $F$

Berechnung der gespiegelten Geraden g' mit einer Hilfsebene $H$

Berechnung der gespiegelten Geraden g' mit einer Hilfsebene $H$