Aufgaben zu Berechnungen am Kreis
- 1
Ermittle die fehlenden Größen in der Tabelle. Runde dabei auf eine Stelle nach dem Komma.
a)
b)
c)
d)
e)
Radius r
4,5 cm
0,7 mm
Durchmesser d
40,0 cm
5,6 m
Umfang U
92,4 m
- 2
Ermittle die fehlenden Größen in der Tabelle (auf die erste Dezimalstelle gerundet).
a)
b)
c)
d)
e)
Radius r
1,5 cm
33,0 cm
Durchmesser d
2,4 m
Umfang U
71,6 m
Flächeninhalt
12,56 cm²
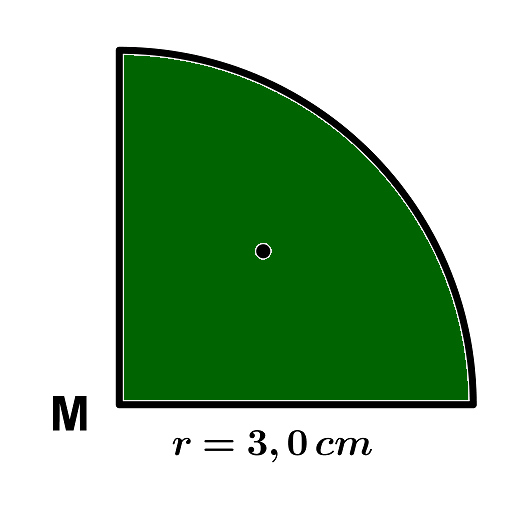
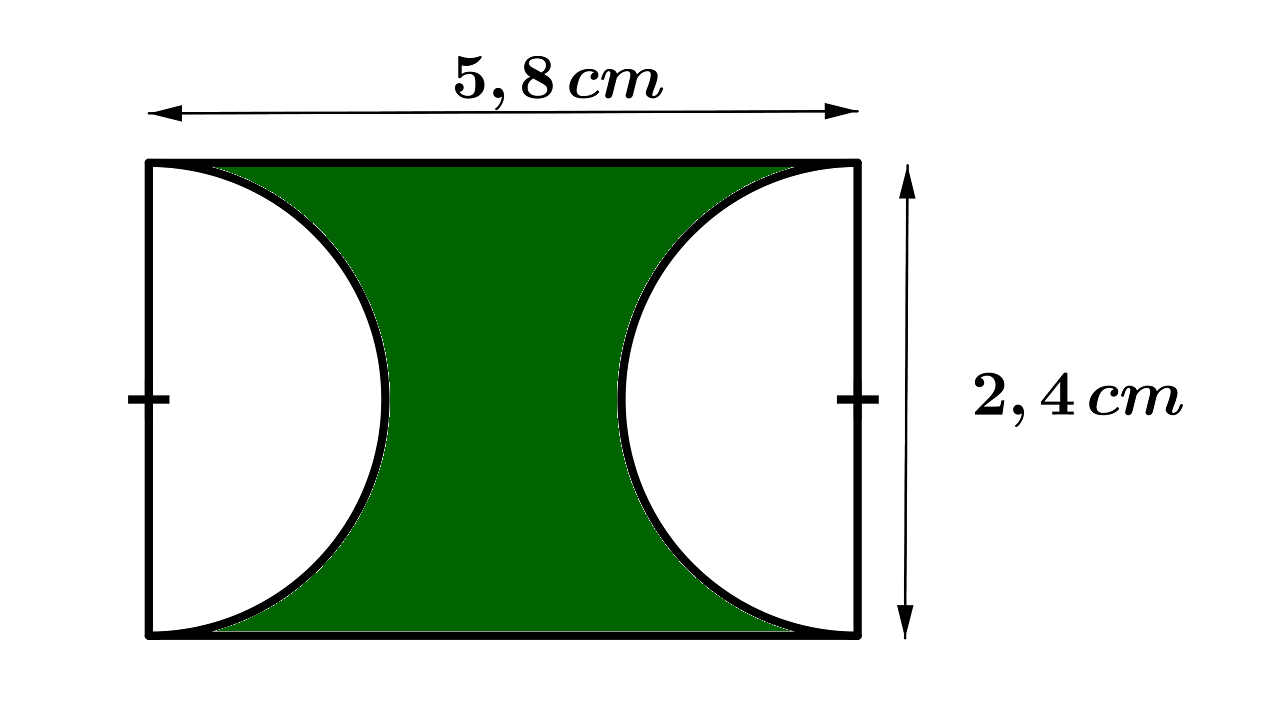
- 3
- 4
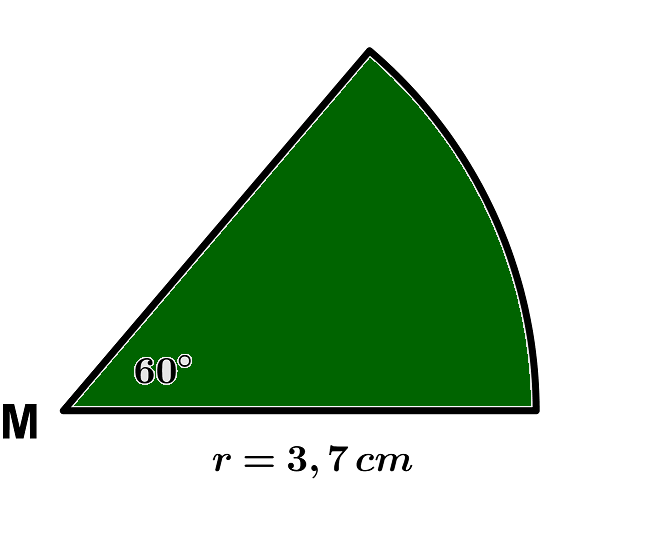
In einem Kreis mit Radius ist ein Sektor mit Mittelpunktswinkel eingezeichnet.
Gib die Fläche des Sektors und die Länge des zugehörigen Bogens an.
- 5
Ein runder Tisch zum Ausziehen hat einen Durchmesser von . Er kann durch rechteckige Einlegeplatten, die jeweils breit sind, vergrößert werden (siehe Skizze).
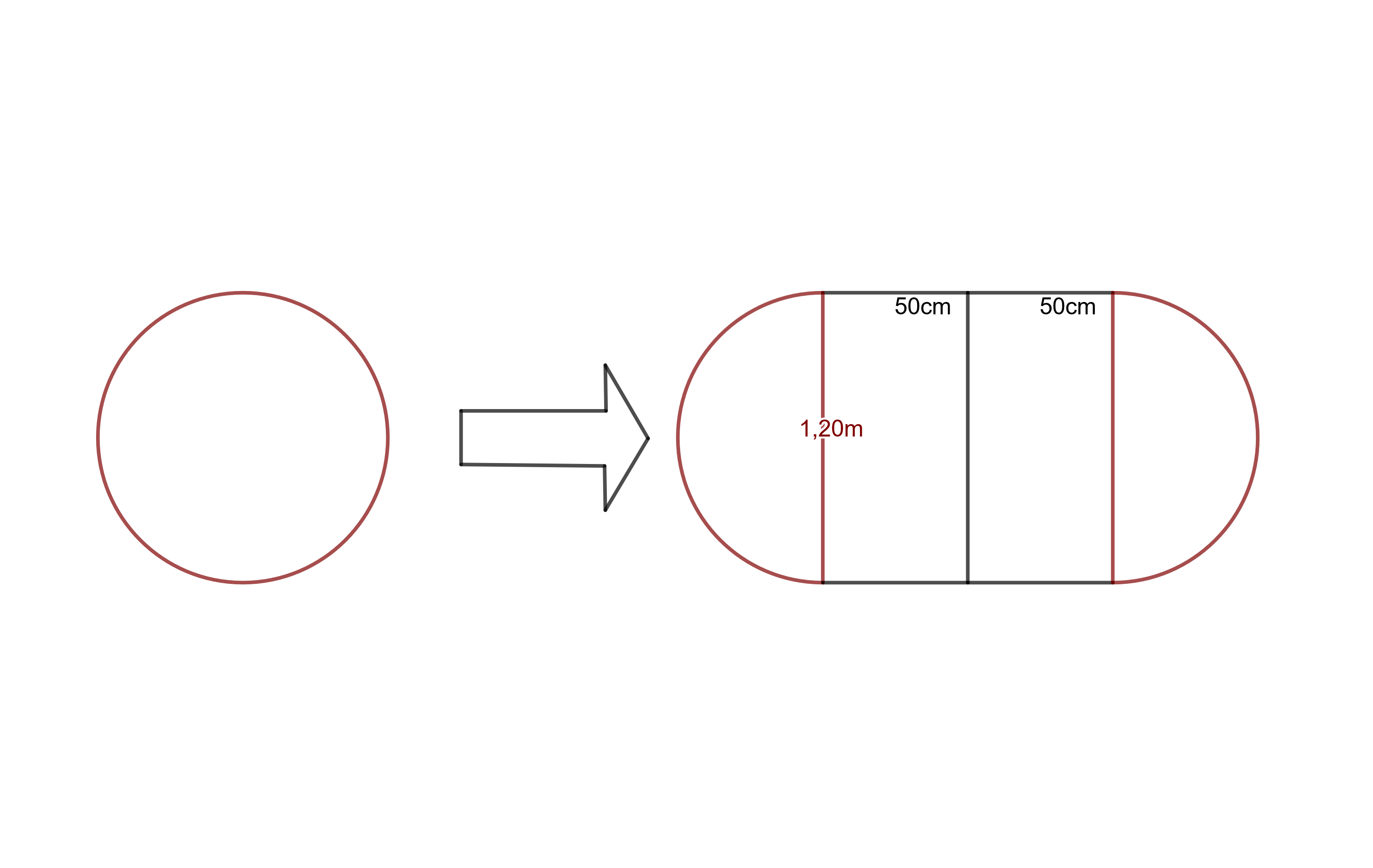
Berechne den Flächeninhalt und den Umfang der vergrößerten Tischplatte.
Für den ausgezogenen Tisch soll eine Tischdecke gekauft werden, die überall mindestens überhängt. Welche der angebotenen Tischdecken eignet sich?
140 cm
260 cm
150 cm
250 cm
160 cm
240 cm
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?