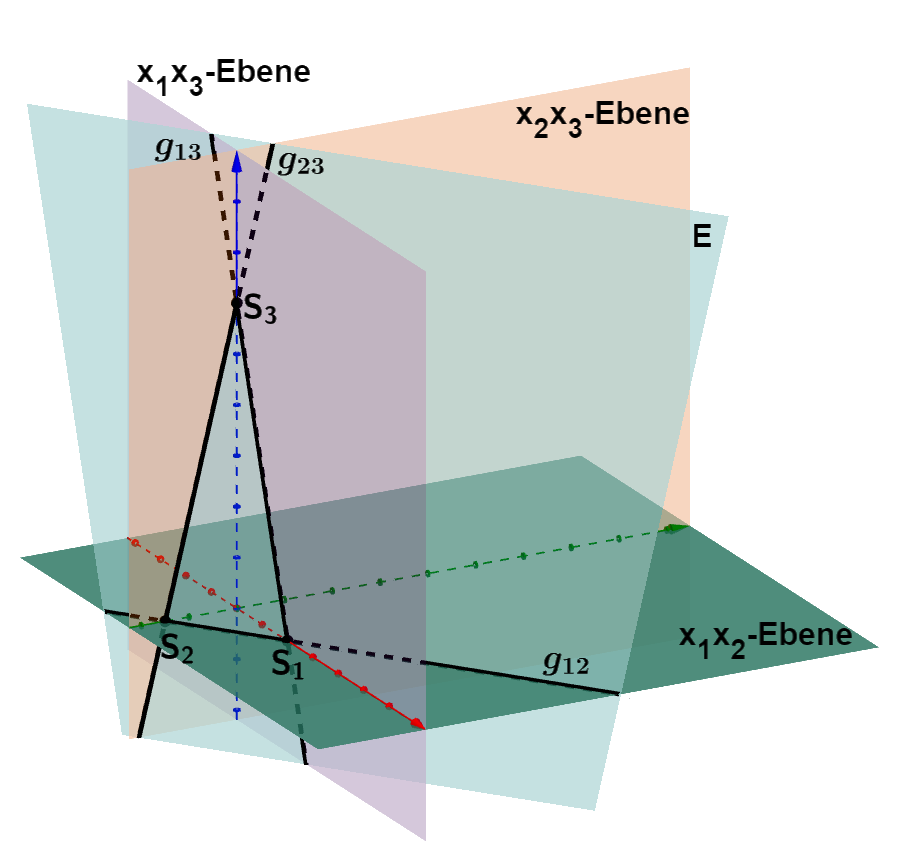
Aufgaben zu Spurpunkten und Spurgeraden einer Ebene

Wie gut kennst du dich aus? Vertiefe dein Wissen mit diesen Aufgaben zu den Spurpunkten und Spurgeraden von Ebenen.

Gegeben ist die Ebene $E:\; 3x_1-4x_2+x_3=12$

Berechne die Spurpunkte der Ebene $E$ .

Bestimme die Spurgeraden der Ebene $E$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Spurgeraden einer Ebene

Spurgerade in der $x_1x_2$ -Ebene

Für die Spurgerade in der $x_1x_2$ -Ebene benötigt man die beiden Spurpunkte $S_{1}$ und $S_2$ , die in Aufgabe a) berechnet worden sind.

$S_1(4|0|0)$ und $S_2(0|-3|0)$

Mit den beiden Punkten $S_{1}$ und $S_{2}$ erstellt man die Gleichung der Spurgeraden in der $x_1x_2$ -Ebene $\;\Rightarrow\;$ $g_{12}:\;\overrightarrow{X}=\overrightarrow{S_1}+r\cdot\left(\overrightarrow{S_2}-\overrightarrow{S_1}\right)$ .

$\displaystyle g_{12}:\;\overrightarrow{X}$	$=$	$\displaystyle \overrightarrow{S_1}+r\cdot\left(\overrightarrow{S_2}-\overrightarrow{S_1}\right)$
	↓	Setze $S_{1}$ und $S_{2}$ ein.
	$=$	$\displaystyle \begin{pmatrix}4 \\ 0 \\ 0 \end{pmatrix}+r\cdot \left(\begin{pmatrix} 0 \\ -3 \\ 0 \end{pmatrix}-\begin{pmatrix} 4 \\0 \\ 0 \end{pmatrix}\right)$
	$=$	$\displaystyle \begin{pmatrix}4 \\ 0 \\ 0 \end{pmatrix}+r\cdot \begin{pmatrix} -4 \\ -3 \\ 0 \end{pmatrix}$

Die Gleichung der Spurgeraden in der $x_1x_2$ -Ebene lautet:

$g_{12}:\;\overrightarrow{X}=\begin{pmatrix}4 \\ 0 \\ 0 \end{pmatrix}+r\cdot \begin{pmatrix} -4 \\ -3 \\ 0 \end{pmatrix}$

Spurgerade in der $x_1x_3$ -Ebene

Für die Spurgerade in der $x_1x_3$ -Ebene benötigt man die beiden Spurpunkte $S_{1}$ und $S_3$ , die in Aufgabe a) berechnet worden sind.

$S_1(4|0|0)$ und $S_3(0|0|12)$

Mit den beiden Punkten $S_{1}$ und $S_{3}$ erstellt man die Gleichung der Spurgeraden in der $x_1x_3$ -Ebene $\;\Rightarrow\;$ $g_{13}:\;\overrightarrow{X}=\overrightarrow{S_1}+r\cdot\left(\overrightarrow{S_3}-\overrightarrow{S_1}\right)$ .

$\displaystyle g_{13}:\;\overrightarrow{X}$	$=$	$\displaystyle \overrightarrow{S_1}+r\cdot\left(\overrightarrow{S_3}-\overrightarrow{S_1}\right)$
	↓	Setze $S_{1}$ und $S_{3}$ ein.
	$=$	$\displaystyle \begin{pmatrix}4 \\ 0 \\ 0 \end{pmatrix}+r\cdot \left(\begin{pmatrix} 0 \\ 0 \\ 12 \end{pmatrix}-\begin{pmatrix} 4 \\0 \\ 0 \end{pmatrix}\right)$
	$=$	$\displaystyle \begin{pmatrix}4 \\ 0 \\ 0 \end{pmatrix}+r\cdot \begin{pmatrix} -4 \\ 0 \\ 12 \end{pmatrix}$

Die Gleichung der Spurgeraden in der $x_1x_3$ -Ebene lautet:

$g_{13}:\;\overrightarrow{X}=\begin{pmatrix}4 \\ 0 \\ 0 \end{pmatrix}+r\cdot \begin{pmatrix} -4 \\ 0\\ 12 \end{pmatrix}$

Spurgerade in der $x_2x_3$ -Ebene

Für die Spurgerade in der $x_2x_3$ -Ebene benötigt man die beiden Spurpunkte $S_{2}$ und $S_3$ , die in Aufgabe a) berechnet worden sind.

$S_2(0|-3|0)$ und $S_3(0|0|12)$

Mit den beiden Punkten $S_{2}$ und $S_{3}$ erstellt man die Gleichung der Spurgeraden in der $x_2x_3$ -Ebene $\;\Rightarrow\;$ $g_{23}:\;\overrightarrow{X}=\overrightarrow{S_2}+r\cdot\left(\overrightarrow{S_3}-\overrightarrow{S_2}\right)$ .

$\displaystyle g_{23}:\;\overrightarrow{X}$	$=$	$\displaystyle \overrightarrow{S_2}+r\cdot\left(\overrightarrow{S_3}-\overrightarrow{S_2}\right)$
	↓	Setze $S_{2}$ und $S_{3}$ ein.
	$=$	$\displaystyle \begin{pmatrix}0 \\ -3 \\ 0 \end{pmatrix}+r\cdot \left(\begin{pmatrix} 0 \\ 0 \\ 12 \end{pmatrix}-\begin{pmatrix} 0 \\-3 \\ 0 \end{pmatrix}\right)$
	$=$	$\displaystyle \begin{pmatrix}0 \\ -3 \\ 0 \end{pmatrix}+r\cdot \begin{pmatrix} 0 \\ 3 \\ 12 \end{pmatrix}$

Die Gleichung der Spurgeraden in der $x_2x_3$ -Ebene lautet:

$g_{23}:\;\overrightarrow{X}=\begin{pmatrix}0 \\ -3 \\ 0 \end{pmatrix}+r\cdot \begin{pmatrix} 0 \\ 3\\ 12 \end{pmatrix}$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Zeichne die Spurpunkte und die Spurgeraden in ein Koordinatensystem.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Spurpunkte einer Ebene
Darstellung der Spurpunkte $S_1$ , $S_2$ und $S_3$ und die entsprechenden Spurgeraden im Koordinatensystem.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

2
Eine Ebene $E$ hat zwei Spurgeraden
$g_{12}: \vec X=\begin{pmatrix}1\\2\\0\end{pmatrix}+r\cdot\begin{pmatrix} 1 \\0 \\0 \end{pmatrix}$ und $g_{23}: \vec X=\begin{pmatrix}0\\2\\2\end{pmatrix}+r\cdot\begin{pmatrix} 0 \\0 \\1 \end{pmatrix}$ .
1. Wie lautet die Gleichung der Ebene $E$ ?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ebene aus 2 Geraden
  Für die Parameterform der Ebene wird ein Stützvektor gewählt, entweder der von $g_{12}$ oder $g_{23}$ und beide Richtungsvektoren der Geraden als Spannvektoren.
  Die Ebene ist damit direkt gegeben durch:
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Zeige, dass die Ebene $E$ keine Spurgerade in der $x_1x_3$ -Ebene besitzt.
  Welche Schlussfolgerung ergibt sich daraus für die Lage dieser Ebene im Koordinatensystem?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Spurgeraden einer Ebene
  Für die Spurgerade (Schnittgerade) der Ebene $E$ mit der $x_1x_3$ -Ebene setzt man $x_2=0$ , da die $x_1x_3$ -Ebene die Gleichung $x_2=0$ hat.
  $\displaystyle x_2$ $=$ $\displaystyle 2+r\cdot 0+s\cdot 0$
  ↓
  Setze $x_2=0$ .
  $\displaystyle 0$ $=$ $\displaystyle 2+r\cdot 0+s\cdot 0$
  Du hast die Gleichung $0=2$ erhalten. Das ist eine falsche Aussage. Es gibt somit keine Schnittgerade mit der $x_1x_3$ -Ebene.
  Die Konsequenz aus dieser Tatsache ist, dass die Ebene $E$ parallel zur $x_1x_3$ -Ebene verläuft.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Eine Ebene $E$ hat die Spurgeraden $g_{12}:\;\overrightarrow{X}=\begin{pmatrix}-1 \\ 0 \\ 0 \end{pmatrix}+r\cdot \begin{pmatrix} 2 \\ 1 \\ 0 \end{pmatrix}$ und $g_{23}:\;\overrightarrow{X}=\begin{pmatrix}0 \\ 0{,}5 \\ 0 \end{pmatrix}+s\cdot \begin{pmatrix} 0 \\ -3 \\ 2 \end{pmatrix}$ :

Bestimme eine Koordinatengleichung der Ebene $E$ und die Gleichung der fehlenden Spurgeraden.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Ebene aus 2 Geraden

Ebenengleichung in Parameterform aufstellen

Für die Parameterform der Ebene wird ein Stützvektor gewählt, entweder der von $g_{12}$ oder von $g_{23}$ und beide Richtungsvektoren der Spurgeraden als Spannvektoren.

Die Ebene ist damit direkt gegeben durch:

\displaystyle E:\overrightarrow{X}=\begin{pmatrix}-1 \\ 0 \\ 0 \end{pmatrix}+r\cdot \begin{pmatrix} 2 \\ 1 \\ 0 \end{pmatrix}+s\cdot \begin{pmatrix} 0 \\ -3 \\ 2 \end{pmatrix}

Umwandlung der Parameterform in die Normalenform

Berechne den Normalenvektor $\vec{n}$ als Vektorprodukt der beiden Richtungsvektoren der Ebene.

$\vec{n}=\begin{pmatrix} 2 \\ 1 \\ 0 \end{pmatrix}\times \begin{pmatrix} 0\\ -3 \\ 2\end{pmatrix}=\begin{pmatrix} 2 \\-4\\ -6 \end{pmatrix}=2\cdot\begin{pmatrix} 1 \\-2\\ -3 \end{pmatrix}$

Für die Ebene in Normalenform $E: \;\left(\overrightarrow{X}-\overrightarrow{A}\right)\circ\vec n =0$ wird noch ein Punkt der Ebene benötigt. Setze $\vec A =\begin{pmatrix}-1\\0\\0\end{pmatrix}$ und den "gekürzten" Normalenvektor $\vec n =\begin{pmatrix} 1 \\-2\\ -3 \end{pmatrix}$ in die Normalenform ein.

$E: \;\left(\overrightarrow{X}-\begin{pmatrix}-1\\0\\0\end{pmatrix}\right)\circ\begin{pmatrix} 1 \\-2\\ -3 \end{pmatrix}=0$

Umwandlung der Normalenform in die Koordinatenform

Berechne das Skalarprodukt:

$\displaystyle E: \;\left(\begin{pmatrix}x_1 \\ x_2\\ x_3 \end{pmatrix}-\begin{pmatrix}-1\\0\\0\end{pmatrix}\right)\circ\begin{pmatrix} 1 \\-2\\ -3 \end{pmatrix}$	$=$	$\displaystyle 0$
	↓	Berechne das Skalarprodukt.
$\displaystyle 1\cdot x_1-2\cdot x_2-3\cdot x_3-((-1)\cdot 1 +0\cdot(-2)+0\cdot(-3)$	$=$	$\displaystyle 0$
$\displaystyle 1\cdot x_1-2\cdot x_2-3\cdot x_3+1$	$=$	$\displaystyle 0$

Die Ebenengleichung $E$ in Koordinatenform lautet: $1\cdot x_1-2\cdot x_2-3\cdot x_3=-1$

Berechnung der fehlenden Spurgeraden

Die fehlende Spurgerade ist die Gerade $g_{13}$ . Diese Gerade liegt in der $x_1x_3$ -Ebene, die die Gleichung $x_2=0$ hat.

Setze $x_2=0$ in der Parameterform der Ebene $E$ und löse die erhaltene Gleichung z.B. nach dem Parameter $r$ auf.

$\displaystyle E:\begin{pmatrix}x_1 \\ x_2\\ x_3 \end{pmatrix}$	$=$	$\displaystyle \begin{pmatrix}-1 \\ 0 \\ 0 \end{pmatrix}+r\cdot \begin{pmatrix} 2 \\ 1 \\ 0 \end{pmatrix}+s\cdot \begin{pmatrix} 0 \\ -3 \\ 2 \end{pmatrix}$
$\displaystyle x_2$	$=$	$\displaystyle 0+r-3s$
	↓	Setze $x_2=0$ .
$\displaystyle 0$	$=$	$\displaystyle r-3s$	$\displaystyle +3s$
	↓	Löse nach r auf.
$\displaystyle 3s$	$=$	$\displaystyle r$

Setze $r=3s$ in die Ebenengleichung ein, um die Gleichung der Spurgeraden $g_{13}$ zu erhalten.

$\displaystyle E:\overrightarrow{X}$	$=$	$\displaystyle \begin{pmatrix}-1 \\ 0 \\ 0 \end{pmatrix}+r\cdot \begin{pmatrix} 2 \\ 1 \\ 0 \end{pmatrix}+s\cdot \begin{pmatrix} 0 \\ -3 \\ 2 \end{pmatrix}$
	↓	Setze $r=3s$ ein.
$\displaystyle g_{13}:\;\overrightarrow{X}$	$=$	$\displaystyle \begin{pmatrix}-1 \\ 0 \\ 0 \end{pmatrix}+3s\cdot \begin{pmatrix} 2 \\ 1 \\ 0 \end{pmatrix}+s\cdot \begin{pmatrix} 0 \\ -3 \\ 2 \end{pmatrix}$
	↓	Fasse zusammen.
	$=$	$\displaystyle \begin{pmatrix}-1 \\ 0 \\ 0 \end{pmatrix}+s\cdot\begin{pmatrix}6+0 \\ 3-3 \\ 0 +2\end{pmatrix}$
	↓	Vereinfache.
	$=$	$\displaystyle \begin{pmatrix}-1 \\ 0 \\ 0 \end{pmatrix}+s\cdot\begin{pmatrix}6 \\0 \\2\end{pmatrix}$

Die fehlende Spurgerade hat die Gleichung $g_{13}:\;\overrightarrow{X}=\begin{pmatrix}-1 \\ 0 \\ 0 \end{pmatrix}+s\cdot\begin{pmatrix}6 \\0 \\2\end{pmatrix}$

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle 3x_1-4x_2+x_3$	$=$	$\displaystyle 12$
	↓	Setze $x_2=x_3=0$ ein.
$\displaystyle 3\cdot x_1-4\cdot 0+0$	$=$	$\displaystyle 12$	$\displaystyle :3$
$\displaystyle x_1$	$=$	$\displaystyle 4$

$\displaystyle 3x_1-4x_2+x_3$	$=$	$\displaystyle 12$
	↓	Setze $x_1=x_3=0$ ein.
$\displaystyle 3\cdot 0-4\cdot x_2+0$	$=$	$\displaystyle 12$	$\displaystyle :(-4)$
$\displaystyle x_2$	$=$	$\displaystyle -3$

$\displaystyle 3x_1-4x_2+x_3$	$=$	$\displaystyle 12$
	↓	Setze $x_1=x_2=0$ ein.
$\displaystyle 3\cdot 0-4\cdot 0+x_3$	$=$	$\displaystyle 12$
$\displaystyle x_3$	$=$	$\displaystyle 12$

Aufgaben zu Spurpunkten und Spurgeraden einer Ebene

Berechnung des Spurpunktes $S_{1}$

Berechnung des Spurpunktes $S_{2}$

Berechnung des Spurpunktes $S_{3}$

Hast du eine Frage oder Feedback?

Spurgerade in der $x_1x_2$ -Ebene

Spurgerade in der $x_1x_3$ -Ebene

Spurgerade in der $x_2x_3$ -Ebene

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Ebenengleichung in Parameterform aufstellen

Umwandlung der Parameterform in die Normalenform

Umwandlung der Normalenform in die Koordinatenform

Berechnung der fehlenden Spurgeraden

$\displaystyle x_2$	$=$	$\displaystyle 2+r\cdot 0+s\cdot 0$
	↓	Setze $x_2=0$ .
$\displaystyle 0$	$=$	$\displaystyle 2+r\cdot 0+s\cdot 0$

Aufgaben zu Spurpunkten und Spurgeraden einer Ebene

Berechnung des Spurpunktes S1​ S_{1}​ S1​​

Berechnung des Spurpunktes S2​ S_{2}​ S2​​

Berechnung des Spurpunktes S3​ S_{3}​ S3​​

Hast du eine Frage oder Feedback?

Spurgerade in der x1x2x_1x_2x1​x2​-Ebene

Spurgerade in der x1x3x_1x_3x1​x3​-Ebene

Spurgerade in der x2x3x_2x_3x2​x3​-Ebene

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Ebenengleichung in Parameterform aufstellen

Umwandlung der Parameterform in die Normalenform

Umwandlung der Normalenform in die Koordinatenform

Berechnung der fehlenden Spurgeraden

Berechnung des Spurpunktes $S_{1}$

Berechnung des Spurpunktes $S_{2}$

Berechnung des Spurpunktes $S_{3}$

Spurgerade in der $x_1x_2$ -Ebene

Spurgerade in der $x_1x_3$ -Ebene

Spurgerade in der $x_2x_3$ -Ebene