Eine Geradenschar ist eine Funktionenschar, die aus unendlich vielen Geraden besteht. Ihr Term ist der einer linearen Funktion mit Parameter.
Aussehen
Bei einer Geradenschar unterscheidet man drei mögliche Szenarien.
Parallelenschar
Alle Repräsentanten aus der Geradenschar sind zueinander parallel und haben keinen gemeinsamen Punkt.
Bei einer Geradenschar ist dies der Fall, wenn alle Repräsentanten die gleiche Steigung haben.
Alle Repräsentanten haben die gleiche Steigung , aber unterschiedliche y-Achsenabschnitte.
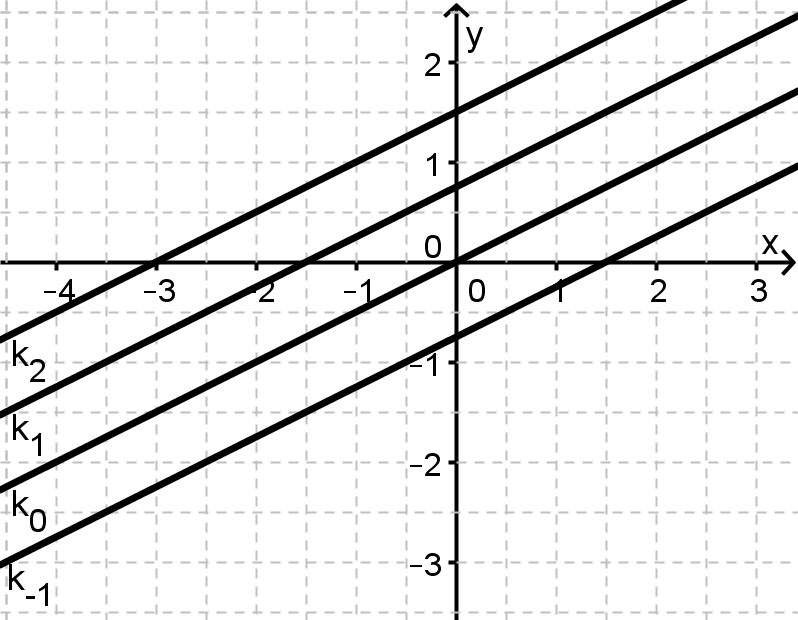
Parallelenschar
Geradenbüschel
Alle Repräsentanten schneiden sich in einem Punkt. Dieser Punkt wird bestimmt, indem man den Schnittpunkt von zwei Repräsentanten bestimmt und diesen zur Probe in die Funktionsgleichung der Geradenschar einsetzt:
Die Geradenschar hat einen Büschelpunkt.
Zur rechnerischen Ermittlung berechnest du den Schnittpunkt der beiden Repräsentanten und :
Setze die beiden Funktionen gleich | |||
| ↓ | |||
Anschließend setzt du den x-Wert in die Geradenschar ein. Fällt dabei der Parameter weg, hast du den Büschelpunkt erfolgreich bestimmt:
Büschelpunkt:
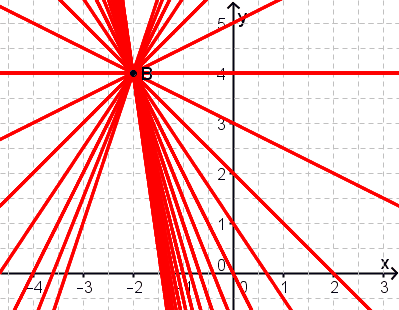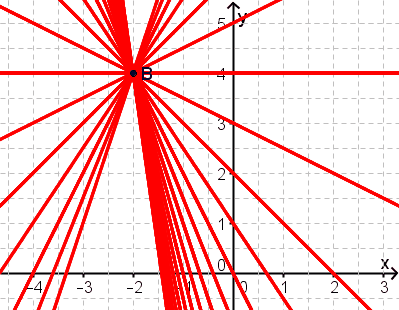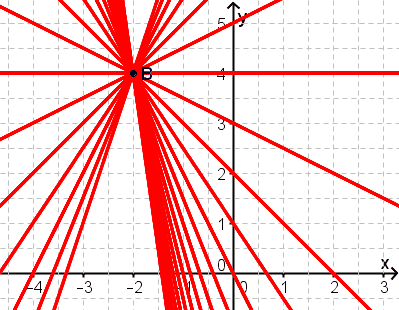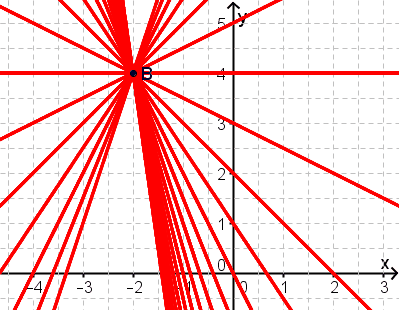
Geradenbüschel
allgemeine Geradenschar
Geradenscharen müssen nicht Parallelenscharen oder Geradenbüschel sein. Wenn sich je zwei Repräsentanten schneiden, aber nicht alle Repräsentanten im gleichen Punkt, handelt es sich um eine allgemeine Geradenschar.
