1 Überblick
In diesem Kurs lernst du nach und nach wichtige Begriffe rund um das Themenfeld Hypothesentest kennen. Dabei arbeitest du mit einem Beispiel "Farben erkennen" und wirst zunächst ohne Hypothesentest die Begriffe Nullhypothese, Gegenhypothese, Stichprobenlänge, kritischer Wert, Entscheidungsregel, An- und Ablehnungsbereich und Fehler 1. und 2. Art kennenlernen.
Am Ende des Kurses kannst du:
Hypothesentests durchführen
Graphisch erklären, was bei einem Hypothesentest passiert
Fehler 1. Art zu vorgegebenen Entscheidungsregeln bestimmen
Voraussetzungen:
Umgang mit einem Tafelwerk oder anderen stochastischen Tabellen
Kursdauer: 45 Min
2 Bist du telepathisch begabt?
Kannst du Farben erkennen, ohne sie zu sehen? Mach das Experiment!
Lege dir vier gleichartige, aber unterschiedlichfarbige Gegenstände zurecht, zum Beispiel vier verschiedenfarbige Buntstifte oder Fineliner. Wichtig ist, dass du durch die Form nicht erkennen kannst, welche Farbe du in der Hand hast.
Schließe nun die Augen und mische die Gegenstände so, dass du nicht mehr sagen kannst, wo welche Farbe liegt.
Wiederhole dann das folgende Experiment 20 Mal:
Ziehe blind einen Gegenstand.
Entscheide dich (immer noch blind) welche Farbe er hat.
Öffne deine Augen und markiere auf einer Strichliste, ob du richtig geraten hast
Lege den Gegenstand zurück und mische.

Vier unterschiedliche Farben, aber identische Stiftform
Was ist bei einem Versuchsdurchlauf (ziehen, raten, überprüfen) die Wahrscheinlichkeit dafür, richtigzuliegen?
Wie viele richtig erratene Gegenstände (=Treffer) würdest du durchschnittlich erwarten?
Ab wie vielen Treffern würdest du nicht mehr von Glück reden?
3 Hypothesen
Wenn du davon ausgehst, dass du telepathisch begabt bist, stellst du damit eine Hypothese (=Vermutung) auf.
Ausgangssituation: Du nennst eine von vier möglichen Farben, jede Farbe ist gleich wahrscheinlich. Also ist die Wahrscheinlichkeit, dass du bei einem Versuch richtig rätst, bzw. . Dies ist die aktuell gültige Hypothese über die Trefferwahrscheinlichkeit. Man nennt sie auch Nullhypothese .
Neue Annahme: Du denkst, dass du telepathisch begabt bist und deshalb mit einer höheren Wahrscheinlichkeit richtig liegst als . Dabei musst du gar nicht sagen, um wie viel (obwohl du es natürlich kannst), sondern stellst lediglich die Gegenhypothese auf: "Ich glaube, dass ich mit mehr als Wahrscheinlichkeit den richtigen Stift finde."
4 Entscheidungsregel
Ab welcher Anzahl richtig erratener Gegenstände würdest du bei einer Stichprobenlänge von 20 Versuchen behaupten, dass es sich nicht um Glück, sondern um Telepathie handelt?
Wo du jetzt ohne weitere Überlegungen die Grenze ziehst und sagst: "Ab dieser Zahl kann man doch nicht mehr von Raten reden!" ist subjektiv. Sagst du zum Beispiel, dass bereits ab 10 erratenen Gegenständen für dich die Gegenhypothese, also Telepathie, die anzunehmende Hypothese ist, kannst du die folgende Entscheidungsregel aufstellen:
Dein kritischer Wert c sind die 10 korrekt erratenen Gegenstände bzw. allgemein deine 10 Treffer.
Der Annahmebereich von der Nullhypothese , also der Bereich, in dem du davon ausgehst, dass nur geraten wurde, ist somit
Der Ablehnungsbereich von der Nullhypothese, also der Bereich, an dem du der Meinung bist, dass die Gegenhypothese eher verwendet werden soll, ist der restliche Bereich .
Optisch kannst du dir das erstmal wie einen Zahlenstrahl vorstellen, der die Länge der Stichprobe, also , hat und der kritische Wert c ist der Wert, der den Zahlenstrahl in zwei Bereiche unterteilt:
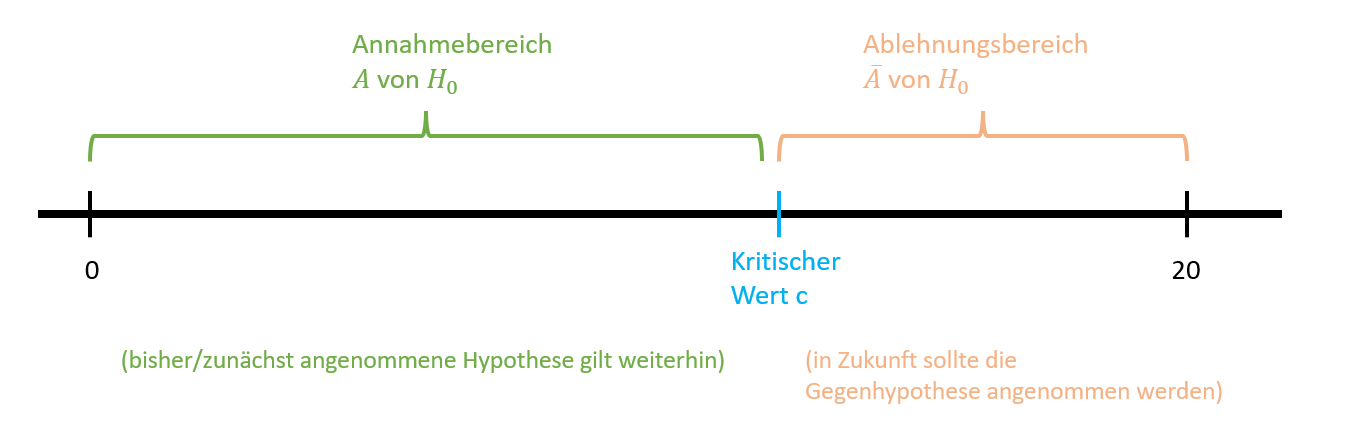
Annahme- und Ablehnungsbereich sind abhängig vom kritischen Wert und der Stichprobenlänge
5 Zugrundeliegende Zufallsgröße
Sich einfach einen kritischen Wert zu überlegen, ist nicht sehr empirisch und natürlich kann in der Forschung nicht so vorgegangen werden! Um besser zu verstehen, wie der kritische Wert bestimmt werden sollte, musst du die grundlegende Situation nochmal mathematischer beleuchten.
Bei diesem Gesamtexperiment handelt es sich um eine Bernoulli-Kette, denn
Jeder einzelne Versuch hat nur zwei mögliche Ergebnisse: Treffer und Nichttreffer
Die Wahrscheinlichkeit für einen Treffer bleibt gleich
Die Reihenfolge der Treffer und Nichttreffer ist egal, es interessiert nur die Anzahl
Aufgrund des dritten Punktes hast du gleichzeitig eine Zufallsgröße : "Anzahl der richtig erratenen Gegenstände". Diese Zufallsgröße ist binomialverteilt mit der Stichprobenlänge und der Trefferwahrscheinlichkeit , wenn man die Nullhypothese, also das Raten annimmt.
Durch obige Feststellung kannst du die Wahrscheinlichkeitsverteilung für (Wahrscheinlichkeit, genau k-mal zu treffen) in einem Histogramm darstellen, zum Beispiel im Tafelwerk die zugehörigen Wahrscheinlichkeiten ablesen oder mit der Bernoulli-Formel selbst berechnen:
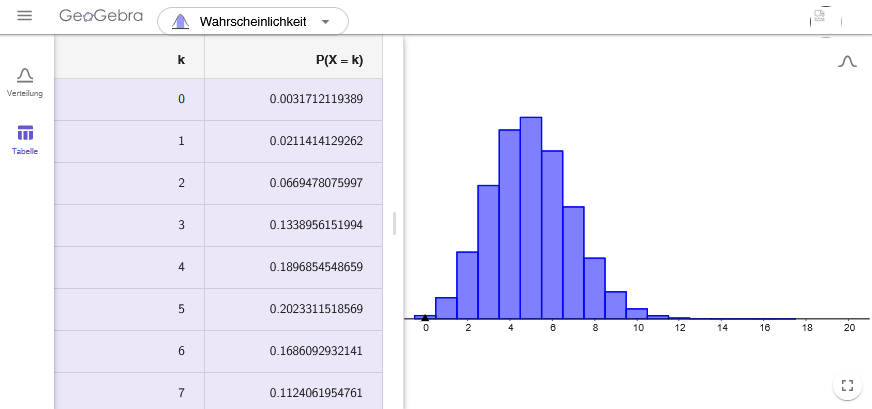
Screenshot aus Geogebra Rechner Suite
Die Verteilung hilft dir, besser einzuschätzen, welche Ereignisse du als wahrscheinlich oder als eher unwahrscheinlich annehmen kannst.
6 Fehlerhafte Annahmen
Das Problem an der ganzen Situation: Man kann nie ausschließen, dass die gewählte Hypothese nicht doch falsch ist. Vielleicht hattest du als Telepath*in heute nur einen schlechten Tag und eigentlich kannst du es wirklich oder du hattest als ratende Person unglaubliches Glück. Selbst wenn man die Stichprobenlänge stark erhöht, kann man nie ausschließen, dass nicht doch versehentlich die falsche Annahme getroffen wird.
Wie wahrscheinlich es ist, dass du dich irrtümlich für eine Hypothese entschieden hast, kannst du bei
Vorgegebenem kritischen Wert
Bekannter Stichprobenlänge und Trefferwahrscheinlichkeit
sogar ganz einfach bestimmen. Dafür brauchst du die kumulierte Wahrscheinlichkeit, also anstelle von bestimmst du (oder je nach Situation auch direkt ).
Du glaubst, dass gilt, also dass die Person nur rät. Du führst den Versuch Mal aus und legst fest, dass ab mindestens Treffern die Hypothese abgelehnt werden soll. Die Wahrscheinlichkeit, dass du die Hypothese ablehnst, also einen Wert erhältst, obwohl nur geraten wurde, ist die Wahrscheinlichkeit , wobei du an der Trefferwahrscheinlichkeit und Stichprobenlänge festhältst.
Die so ermittelte Wahrscheinlichkeit für eine Fehlentscheidung nennt man Fehler 1. Art oder -Fehler.
Hypothese gilt | Gegenhypothese gilt | |
|---|---|---|
wird als gültig angenommen | Richtige Entscheidung! | Man geht von aus, obwohl gilt. wird also irrtümlich abgelehnt. Fehler 2. Art oder -Fehler |
wird als gültig angenommen | Man geht von aus, obwohl gilt, wird also irrtümlich abgelehnt. Fehler 1. Art oder -Fehler | Richtige Entscheidung! |
7 Signifikanzniveau und Signifikanztest
Empirischer, als den kritischen Wert selbst festzulegen, ist es, sich eine Irrtumswahrscheinlichkeit zu überlegen, die man verkraften kann und den kritischen Wert zu dieser Irrtumswahrscheinlichkeit zu bestimmen. Sagen wir, du möchtest mit deinem telepathischen Talent in eine Talkshow. Das Produktionsteam könnte jetzt vorgeben: "Du darfst nur in der Show auftreten, wenn die Wahrscheinlichkeit dafür, dass wir irrtümlich davon ausgehen, dass du nicht rätst, bei 20 Versuchen höchstens beträgt."
Die stehen dabei für den -Fehler (Fehler 1. Art) und beschreiben die Wahrscheinlichkeit dafür, dass die Nullhypothese abgelehnt wird, obwohl sie gilt. Gibt man den -Fehler fest vor, wie es beim Signifikanztest immer der Fall ist, wird er häufig auch als Irrtumswahrscheinlichkeit oder Signifikanzniveau bezeichnet.
Je kleiner man das Signifikanzniveau wählt, desto unwahrscheinlicher ist es, dass man mit seiner Hypothese falsch liegt. Allerdings ist der Test dann eventuell nicht brauchbar, weil man zum Beispiel zu wenig Risiken eingeht.
8 Hypothesentest durchführen
Um den kritischen Wert c zu bestimmen beziehungsweise die Entscheidungsregel abhängig von einem Signifikanzniveau aufzustellen, gehst du folgendermaßen vor:
Testgröße, Stichprobenlänge und Signifikanzniveau definieren
Hypothesen mit Trefferwahrscheinlichkeit aufstellen
Annahme und Ablehnungsbereich in Abhängigkeit von aufstellen (Entscheidung linksseitiger oder rechtsseitiger Hypothesentest)
Term zur "Berechnung" von angeben und ggf. vereinfachen
kritischen Wert z.B. mithilfe vom Tafelwerk bestimmen
Entscheidungsregel angeben und ggf. weiterführende Fragen beantworten.
Du schaffst es bei 20 Versuchen 10 Objekte korrekt zu erkennen. Würdest du in die Talkshow eingeladen werden, wenn das Signifikanzniveau 5% beträgt?
Testgröße: T: "Anzahl der korrekt erratenen Gegenstände"
Stichprobenlänge: 20 Versuche
Hypothesen und Entscheidungsregel in Abhängigkeit von :
Nullhypothese | Gegenhypothese | |
|---|---|---|
In Worten | Person rät nur (Standardfall) | Person kann häufiger als erwartet blind die Farbe erkennen |
mit Trefferwahrscheinlichkeit p | ||
Als Annahme- bzw. Ablehnungsbereich in Abhängigkeit von c |
Term zur Berechnung von :
ist die maximale Wahrscheinlichkeit, dass man einen Wert in erhält (also in diesem Fall ) und trotzdem die Hypothese gilt:
| ↓ | Es können nur kummulierte Wahrscheinlichkeiten der Form . Benutze das Gegenereignis | ||
| ↓ | statt kannst du auch schreiben | ||
| ↓ | z.B. im Tafelwerk schlägst du nach, wann die kummulierte Wahrscheinlichkeit letztmals unter 0,95 liegt. | ||
Im Tafelwerk oder anderen tabellarischen Übersichten nimmst du am besten ein Lineal und schiebst dieses so lange nach unten zu größeren Werten von , bis du die 95% erreichst. Der letzte Wert unter 0,95 ist die obere Grenze des Annahmebereichs, der erste darüber ist die untere Grenze des Ablehnungsbereichs. So erhältst du:
und mit den 10 geglückten Versuchen würdest du in die Sendung eingeladen werden!
Die meisten Fehler passieren an der Grenze von und , nämlich bei der Frage, ob der kritische Wert gerade noch in liegt oder bereits in . Nimm dir für diese Entscheidung immer nochmal einen Atemzug Zeit und überprüfe, ab wann die geforderte Wahrscheinlichkeit wirklich überschritten wurde.
9 Hilfestellung: Graphische Darstellung
Da die Testgröße binomialverteilt ist, kann mithilfe verschiedener Werkzeuge, wie zum Beispiel GeoGebra, auch leicht die Verteilungskurve in einem Histogramm geplottet werden.
Graphisch ist der Hypothesentest dann so zu verstehen:
Du legst Stichprobenlänge und Trefferwahrscheinlichkeit fest und lässt dir damit das Histogramm generieren
Du entscheidest abhängig von der Nullhypothese, ob der Bereich, indem die Nullhypothese abgelehnt werden soll, am linken Rand oder am rechten Rand ist. Je nachdem ist es ein links- oder rechtsseitiger Test.
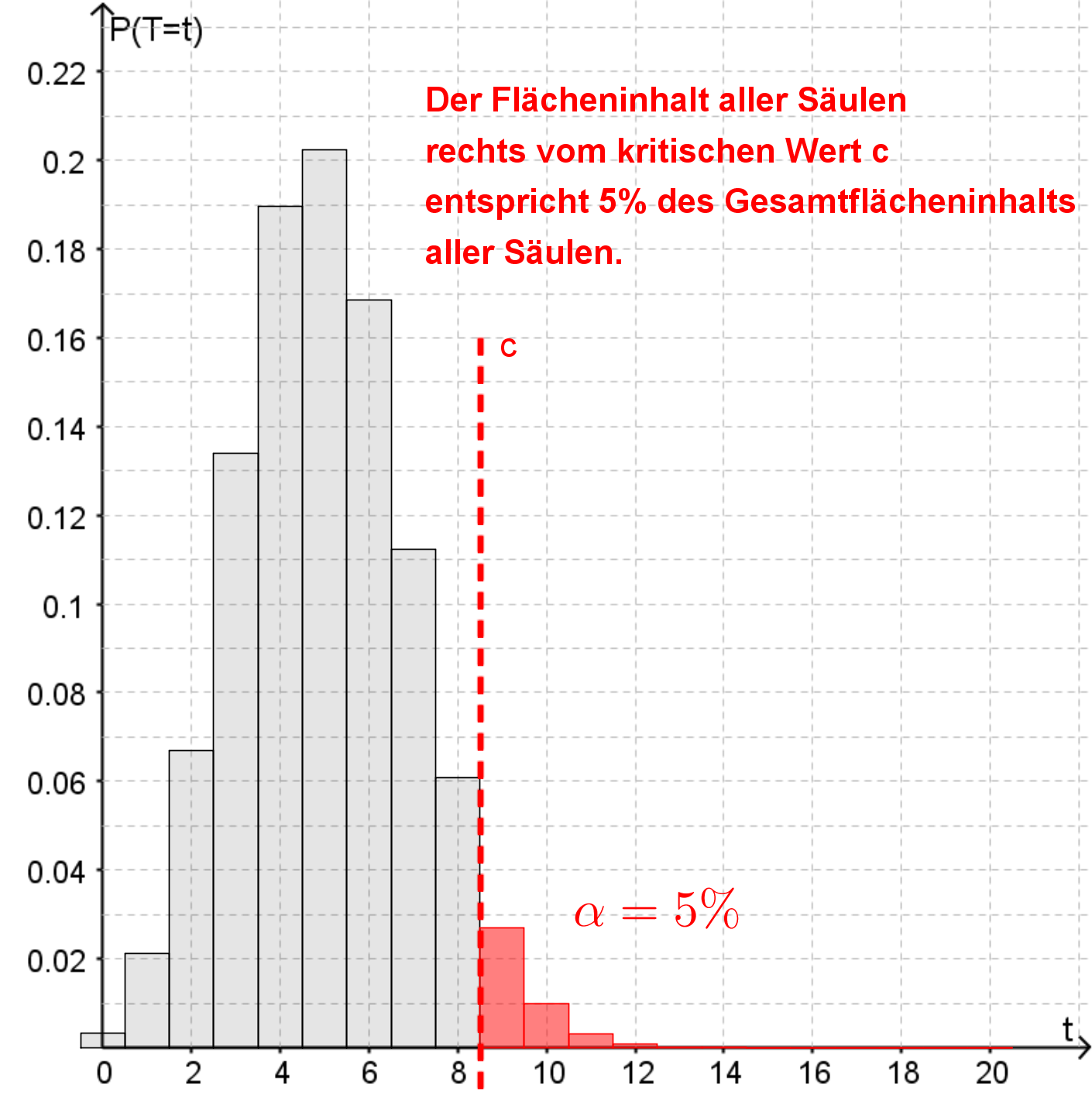
Du suchst den kritischen Wert , unter dem/ab dem die restlichen Wahrscheinlichkeiten nur noch (Signifikanzniveau) ist.
Häufig ist das Signifikanzniveau und du fragst dich nur noch "Was ist , was ist , schneide ich links oder rechts die ab?" und kannst dann deinen kritischen Wert daraus bestimmen.
Probier es für die Beispielaufgabe im Applet aus!
Stelle zunächst die Stichprobenlänge ein. Außerdem hast du festgelegt, dass die Nullhypothese : "Person rät nur" die Trefferwahrscheinlichkeit hat. Das Signifikanzniveau wurde auf festgelegt.
Die Hypothese musst du ablehnen, wenn die Person besonders viele Gegenstände richtig errät. Der Ablehnungsbereich ist also im oberen Teil der Stichprobe und es handelt sich somit um einen rechtsseitigen Test. Der Ablehnungsbereich wird dir im Applet schon automatisch angezeigt, mit dem blauen Schieberegler kannst du dir die kumulierten Wahrscheinlichkeiten aber auch nochmal anzeigen lassen.
Laden
10 Links- und rechtsseitiger Test
Gerade fiel schon der Begriff "rechtsseitiger Test" und im Applet hast du auch die Auswahl "linksseitiger Test" und "rechtsseitiger Test" bekommen. Wenn du eine graphische Vorstellung vom Test hast, ist diese Unterscheidung leicht zu treffen. Es geht nämlich lediglich um die Frage, ob der Ablehnungsbereich auf der linken Seite der Kurve oder auf der rechten Seite der Kurve ist und ob man im Tafelwerk bei der kumulierten Wahrscheinlichkeit sucht oder .
Mehr dazu gibt es bei den Hypothesentest-Arten.
11 Beispielaufgabe linksseitiger Test
Der linksseitige Hypothesentest wird häufig als leichter angesehen, da man direkt die kumulierte Wahrscheinlichkeit nachschauen kann, ohne zuvor umzuformen. Versuche doch mal die folgende Aufgabe nach dem erarbeiteten Schema zu lösen:
Laden
Zur Hilfestellung kannst du vorab oder zur Kontrolle nochmal das Geogebra-Applet verwenden:
12 Zusammenfassung
Sich zu irren kann je nach Branche teuer oder tödlich sein. Kein Risiko einzugehen oder auf falschen Annahmen zu beharren, kann aber den gleichen Effekt haben. Der Hypothesentest ist ein statistischer Test, mit dem die Wahrscheinlichkeit, sich zu irren, von Beginn an vorgegeben und so abgeschätzt wird. Um einen links- oder rechtsseitigen Hypothesentest durchzuführen, gehst du folgendermaßen vor:
Testgröße, Stichprobenlänge und Signifikanzniveau definieren
Hypothesen mit Trefferwahrscheinlichkeit aufstellen
Annahme und Ablehnungsbereich in Abhängigkeit von aufstellen (Entscheidung linksseitiger oder rechtsseitiger Hypothesentest)
Term zur "Berechnung" von angeben und ggf. vereinfachen
kritischen Wert z.B. mithilfe vom Tafelwerk bestimmen
Entscheidungsregel angeben und ggf. weiterführende Fragen beantworten.
Graphisch verbirgt sich hinter dem Hypothesentest eine Binomialverteilung, also eine glockenartige Kurve (die aber nicht im Zentrum der Stichprobe liegen muss!) und die Suche nach einem kritischen Wert auf der linken oder rechten Seite der Kurve, der den Annahme- bzw. Ablehnungsbereich definiert. Der Flächeninhalt aller Säulen im Histogramm, die im Ablehnungsbereich liegen, entsprechen dem Signifikanzniveau .
