Geometrie, Teil B, Aufgabengruppe 1

Gegeben sind die Punkte $A (19 | 0 | 0)$ , $B (0 | 19 | 0)$ , $E (12 | 0 | 7)$ und $F (0 | 12 | 7)$

(vgl. Abbildung 1). Das Viereck $A B F E$ liegt in der Ebene $L$ .

Weisen Sie nach, dass das Viereck $A B F E$ ein Trapez mit zwei gleich langen Seiten ist. (3 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Trapez
Ist das Viereck ist ein Trapez?
Ein Trapez ist ein Viereck, bei dem zwei gegenüberliegende Seiten parallel zueinander sind.
Aus der Abbildung 1 folgt, dass (vermutlich) $\vec{A B} ∥ \vec{E F}$ .
Berechne die Vektoren $\vec{A B}$ und $\vec{E F}$ und überprüfe sie auf Parallelität.
$\vec{A B} = \vec{B} - \vec{A} = (\begin{array}{c} 0 \\ 19 \\ 0 \end{array}) - (\begin{array}{c} 19 \\ 0 \\ 0 \end{array}) = (\begin{array}{c} - 19 \\ 19 \\ 0 \end{array})$
$\vec{E F} = \vec{F} - \vec{E} = (\begin{array}{c} 0 \\ 12 \\ 7 \end{array}) - (\begin{array}{c} 12 \\ 0 \\ 7 \end{array}) = (\begin{array}{c} - 12 \\ 12 \\ 0 \end{array})$
Die Vektoren $\vec{A B}$ und $\vec{E F}$ sind parallel zueinander, wenn sie Vielfache voneinander sind, d.h. wenn $\vec{A B} = k \cdot \vec{E F}$ .
$(\begin{array}{c} - 19 \\ 19 \\ 0 \end{array}) = k \cdot (\begin{array}{c} - 12 \\ 12 \\ 0 \end{array}) \Rightarrow k = \frac{19}{12} (gilt für alle 3 Gleichungen)$
Somit folgt:
Die Vektoren $\vec{A B}$ und $\vec{E F}$ sind parallel zueinander und das Viereck $A B F E$ ist ein Trapez.
Das Trapez hat zwei gleich lange Seiten
Aus der Abbildung 1 folgt, dass (vermutlich) $| \vec{A E} | = | \vec{B F} |$ .
Berechne die Vektoren $\vec{A E}$ und $\vec{B F}$ und überprüfe sie auf gleiche Länge.
$\vec{A E} = \vec{E} - \vec{A} = (\begin{array}{c} 12 \\ 0 \\ 7 \end{array}) - (\begin{array}{c} 19 \\ 0 \\ 0 \end{array}) = (\begin{array}{c} - 7 \\ 0 \\ 7 \end{array})$
$\vec{B F} = \vec{F} - \vec{B} = (\begin{array}{c} 0 \\ 12 \\ 7 \end{array}) - (\begin{array}{c} 0 \\ 19 \\ 0 \end{array}) = (\begin{array}{c} 0 \\ - 7 \\ 7 \end{array})$
Für den Betrag gilt:
$| \vec{A E} | = \sqrt{(- 7)^{2} + 0^{2} + 7^{2}} = \sqrt{98}$
$| \vec{B F} | = \sqrt{0^{2} + (- 7)^{2} + 7^{2}} = \sqrt{98}$
$\Rightarrow | \vec{A E} | = | \vec{B F} |$
Damit ist nachgewiesen, dass das Viereck $A B F E$ ein Trapez mit zwei gleich langen Seiten ist.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Bestimmen Sie eine Gleichung von $L$ in Koordinatenform sowie die Größe $φ$ des Winkels, den $L$ mit der $x_{1} x_{2}$ -Ebene einschließt. (6 P)
(zur Kontrolle: $x_{1} + x_{2} + x_{3} - 19 = 0; φ = 55 °)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Koordinatenform
Eine Gleichung von $L$ in Koordinatenform
Erstelle zunächst die Ebenengleichung $L$ in Parameterform:
$L = E_{A B E} : \vec{X} = \vec{O A} + r \cdot \vec{A B} + s \cdot \vec{A E}$
$L : \vec{X} = (\begin{array}{c} 19 \\ 0 \\ 0 \end{array}) + r \cdot (\begin{array}{c} - 19 \\ 19 \\ 0 \end{array}) + s \cdot (\begin{array}{c} - 7 \\ 0 \\ 7 \end{array})$
Berechne den Normalenvektor der Ebene $L$ über das Kreuzprodukt der beiden Richtungsvektoren von $L$ .
$\vec{n} = (\begin{array}{c} - 19 \\ 19 \\ 0 \end{array}) \times (\begin{array}{c} - 7 \\ 0 \\ 7 \end{array}) = (\begin{array}{c} 133 \\ 133 \\ 133 \end{array}) = 133 \cdot (\begin{array}{c} 1 \\ 1 \\ 1 \end{array})$
Benutze den verkürzten Normalenvektor ${\vec{n}}_{L} = (\begin{array}{c} 1 \\ 1 \\ 1 \end{array})$ .
Für die Normalenform gilt:
$L : (\vec{X} - \vec{A}) \circ \vec{n}$ $=$ $0$
↓
Setze $\vec{A}$ und $\vec{n}$ ein.
$(\vec{X} - (\begin{array}{c} 19 \\ 0 \\ 0 \end{array})) \circ (\begin{array}{c} 1 \\ 1 \\ 1 \end{array})$ $=$ $0$
Wandle die Normalenform in die Koordinatenform um, indem das Skalarprodukt berechnet wird:
$((\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}) - (\begin{array}{c} 19 \\ 0 \\ 0 \end{array})) \circ (\begin{array}{c} 1 \\ 1 \\ 1 \end{array})$ $=$ $0$
↓
Berechne das Skalarprodukt.
$x_{1} \cdot 1 + x_{2} \cdot 1 + x_{3} \cdot 1 - (19 \cdot 1 + 0 \cdot 1 + 0 \cdot 1)$ $=$ $0$
↓
Fasse zusammen.
$x_{1} + x_{2} + x_{3} - 19$ $=$ $0$
Die Gleichung der Ebene $L$ lautet:
$L : x_{1} + x_{2} + x_{3} - 19 = 0$
Berechnung der Größe $φ$ des Winkels, den $L$ mit der $x_{1} x_{2}$ -Ebene einschließt
Der Normalenvektor der Ebene $L$ ist ${\vec{n}}_{L} = (\begin{array}{c} 1 \\ 1 \\ 1 \end{array})$ und der Normalenvektor der $x_{1} x_{2}$ -Ebene ist ${\vec{n}}_{x_{1} x_{2}} = (\begin{array}{c} 0 \\ 0 \\ 1 \end{array})$ .
Der Betrag von Vektor ${\vec{n}}_{L}$ ist $| {\vec{n}}_{L} | = \sqrt{1^{2} + 1^{2} + 1^{2}} = \sqrt{3}$ .
Der Betrag von Vektor ${\vec{n}}_{x_{1} x_{2}}$ ist $| {\vec{n}}_{x_{1} x_{2}} | = \sqrt{0^{2} + 0^{2} + 1^{2}} = \sqrt{1} = 1$ .
Dann berechnet sich der Winkel zwischen den beiden Ebenen mit der Formel
$\cos (φ) = \frac{{\vec{n}}_{L} \circ {\vec{n}}_{x_{1} x_{2}}}{| {\vec{n}}_{L} | \cdot | {\vec{n}}_{x_{1} x_{2}} |}$
.
$\cos (φ)$ $=$ $\frac{{\vec{n}}_{L} \circ {\vec{n}}_{x_{1} x_{2}}}{| {\vec{n}}_{L} | \cdot | {\vec{n}}_{x_{1} x_{2}} |}$
↓
Setze die Vektoren und ihre Beträge ein.
$=$ $\frac{(\begin{array}{c} 1 \\ 1 \\ 1 \end{array}) \circ (\begin{array}{c} 0 \\ 0 \\ 1 \end{array})}{\sqrt{3} \cdot 1}$
↓
Berechne das Skalarprodukt.
$=$ $\frac{1 \cdot 0 + 1 \cdot 0 + 1 \cdot 1}{\sqrt{3} \cdot 1}$
↓
Vereinfache.
$=$ $\frac{1}{\sqrt{3}}$
Den Winkel $φ$ erhält man durch Anwendung der trigonometrischen Umkehrfunktion.
$φ$ $=$ $\cos^{- 1} (\frac{1}{\sqrt{3}})$
$\approx$ ${54,74}^{\circ}$
Die Größe $φ$ des Winkels, den $L$ mit der $x_{1} x_{2}$ -Ebene einschließt beträgt etwa $55^{\circ}$ (entspricht der Kontrollangabe).
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Abbildung 1 zeigt den Körper $A B C D E F G H$ , bei dem die quadratische Grundfläche $A B C D$ parallel zur quadratischen Deckfläche $E F G H$ liegt. Der Körper ist symmetrisch sowohl bezüglich der $x_{1} x_{3}$ -Ebene als auch bezüglich der $x_{2} x_{3}$ -Ebene. Außerdem werden die Punkte $S_{k} (0 | 0 | k)$ mit $k \in] 7; + \infty [$ betrachtet, die Spitzen von Pyramiden $E F G H S_{k}$ sind.
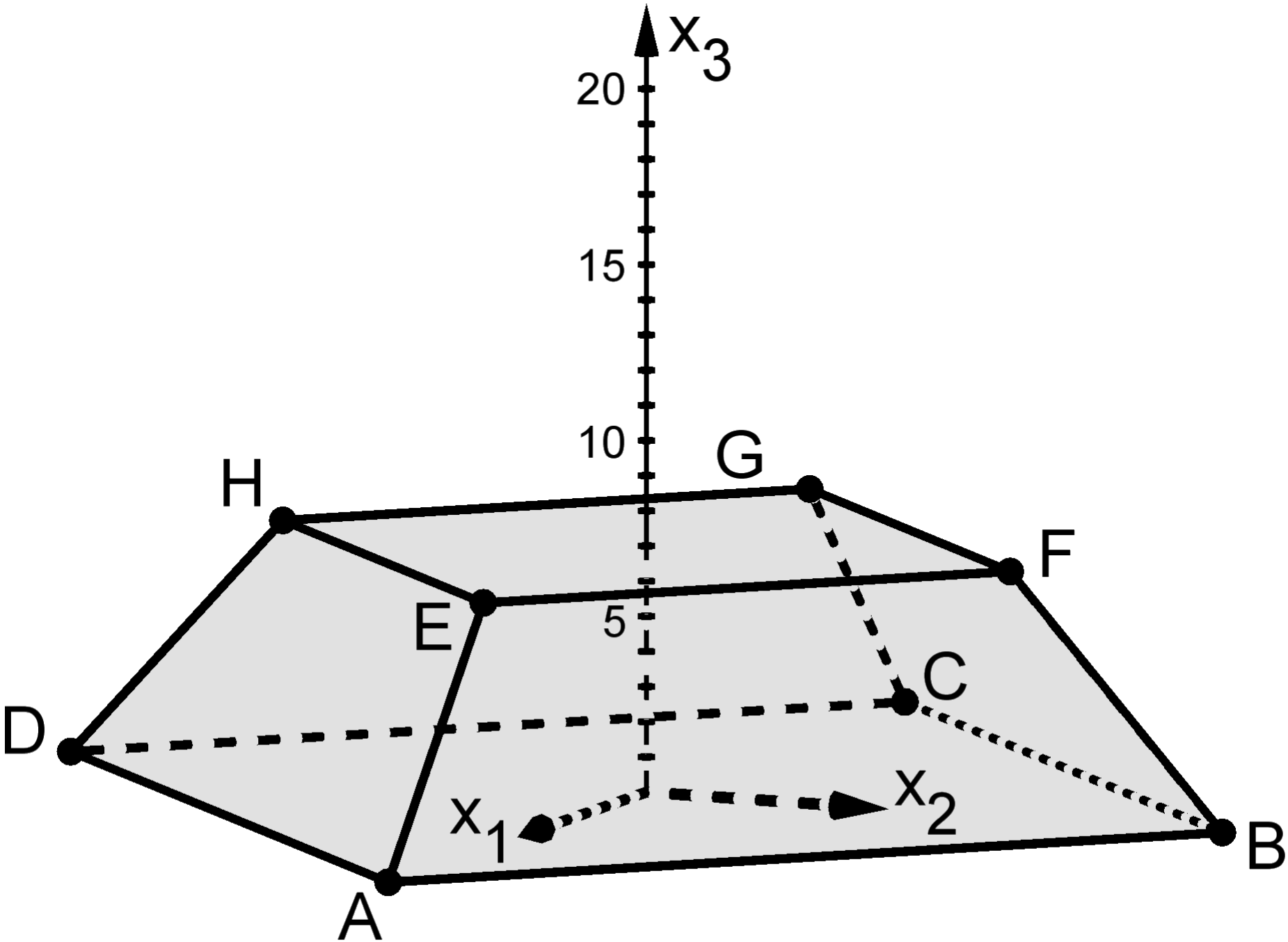
Abb. 1
Bestimmen Sie rechnerisch denjenigen Wert von $k$ , für den die Pyramide $E F G H S_{k}$ den Körper $A B C D E F G H$ zu einer großen Pyramide $A B C D S_{k}$ ergänzt. (2 P)
(zur Kontrolle: $k = 19$ )

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung in der analytischen Geometrie
Die Spitze $S_{k}$ muss auf der Geraden durch die Punkte $A$ und $E$ liegen.
Erstelle die Geradengleichung $g_{A E} : \vec{X} = \vec{A} + r \cdot \vec{A E}$ .
Setze $\vec{A} = (\begin{array}{c} 19 \\ 0 \\ 0 \end{array})$ und $\vec{A E} = (\begin{array}{c} - 7 \\ 0 \\ 7 \end{array})$ in die Geradengleichung ein.
$g_{A E} : \vec{X} = (\begin{array}{c} 19 \\ 0 \\ 0 \end{array}) + r \cdot (\begin{array}{c} - 7 \\ 0 \\ 7 \end{array})$
$S_{k} \in g_{A E}$
$(\begin{array}{c} 0 \\ 0 \\ k \end{array})$ $=$ $(\begin{array}{c} 19 \\ 0 \\ 0 \end{array}) + r \cdot (\begin{array}{c} - 7 \\ 0 \\ 7 \end{array})$
Die erste Gleichung liefert $0 = 19 - 7 r \Rightarrow r = \frac{19}{7}$ .
Die dritte Gleichung lautet $k = 7 r$ .
Setze $r = \frac{19}{7}$ ein $\Rightarrow k = 7 \cdot \frac{19}{7} = 19$
Für $k = 19$ ergänzt die Pyramide $E F G H S_{19}$ den Körper $A B C D E F G H$ zu einer großen Pyramide $A B C D S_{19}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
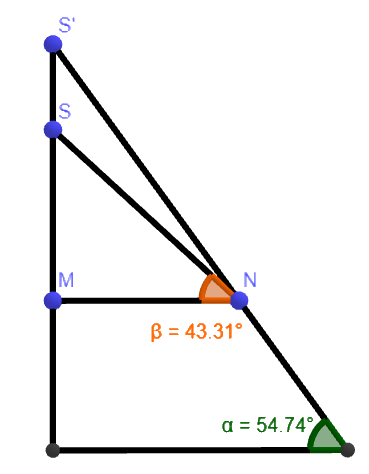
Zeichnen Sie die Pyramide $E F G H S_{15}$ in Abbildung 1 ein. Die Seitenfläche $E F S_{15}$ und die Grundfläche $E F G H$ dieser Pyramide schließen einen Winkel ein. Begründen Sie ohne weitere Rechnung, dass die Größe dieses Winkels kleiner als $45 °$ ist; verwenden Sie dazu folgende Information:
Für den Mittelpunkt $M$ des Quadrats $E F G H$ und den Punkt $N$ mit
$\vec{N} = \frac{1}{2} \cdot (\vec{E} + \vec{F})$ gilt $M S_{15} < M N .$ (4 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Trigonometrische Funktion
In der Abbildung ist in der (halben) Seitenansicht sowohl die Pyramide mit der Spitze $S^{'} (0 | 0 | 19)$ als auch die Knickpyramide mit der Spitze $S (0 | 0 | 15)$ und die beiden Punkte $M$ und $N$ dargestellt. Der Winkel $∡ N M S$ beträgt $90^{\circ}$ .
Aus der Aufgabenstellung entnimmt man, dass $M S_{15} < M N$ ist.
Wäre $M S_{15} = M N$ , dann wäre der Winkel $∡ S N M = 45^{\circ}$ , da der $\tan (∡ S N M) = \frac{M S_{15}}{M N} = 1$ ist.
Da aber $M S_{15} < M N$ gegeben ist, muss der $\tan (∡ S N M) = \frac{M S_{15}}{M N} < 1$ sein, d.h. der Winkel $∡ S N M < 45^{\circ}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Der Körper $A B C D E F G H S_{15}$ stellt modellhaft die Knickpyramide des Pharaos Snofru dar, die ca. 2650 v. Chr. in Ägypten erbaut wurde (vgl. Abbildung 2). Dabei beschreibt die $x_{1} x_{2}$ -Ebene den horizontalen Boden; eine Längeneinheit im Koordinatensystem entspricht $7 m$ in der Realität.
Abb. 2
Ursprünglich wurde mit dem Bau einer Pyramide begonnen, die im Modell der Pyramide $A B C D S_{19}$ entspricht. Aufgrund von Stabilitätsproblemen im Bauprozess musste die Neigung der Seitenflächen gegenüber dem Boden beim Erreichen einer bestimmten Höhe verändert werden. Der entstandene Knick ist namensgebend für die Pyramide.
Bestimmen Sie die Höhenänderung des Bauwerks, die durch die Bauplanänderung hervorgerufen wurde, in Metern. Begründen Sie, dass im unteren Teil des Bauwerks der Neigungswinkel der Seitenflächen gegenüber dem Boden um mehr als $9^{\circ}$ größer ist als im oberen Teil des Bauwerks. (3 P)

Höhendifferenz
Eine Längeneinheit im Koordinatensystem entspricht $7 m$ in der Realität
Mit der Spitze $S_{19}$ beträgt die Pyramidenhöhe $h = 19 LE = 19 \cdot 7 m = 133 m$ .
Mit der Spitze $S_{15}$ beträgt die Pyramidenhöhe $h^{'} = 15 LE = 15 \cdot 7 m = 105 m$ .
Die Höhendifferenz beträgt $△ h = h - h^{'} = 133 m - 105 m = 28 m$ .
Im unteren Teil des Bauwerks ist der Neigungswinkel der Seitenflächen gegenüber dem Boden um mehr als $9^{\circ}$ größer, als im oberen Teil des Bauwerks.
In Aufgabe d) ist gezeigt worden, dass der obere Winkel kleiner als $45^{\circ}$ ist.
In Aufgabe b) ist gezeigt worden, dass der untere Winkel etwa $55^{\circ}$ beträgt.
Also ist der Neigungswinkel im unteren Teil des Bauwerks um mehr als $9^{\circ}$ größer als der Winkel im oberen Teil.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
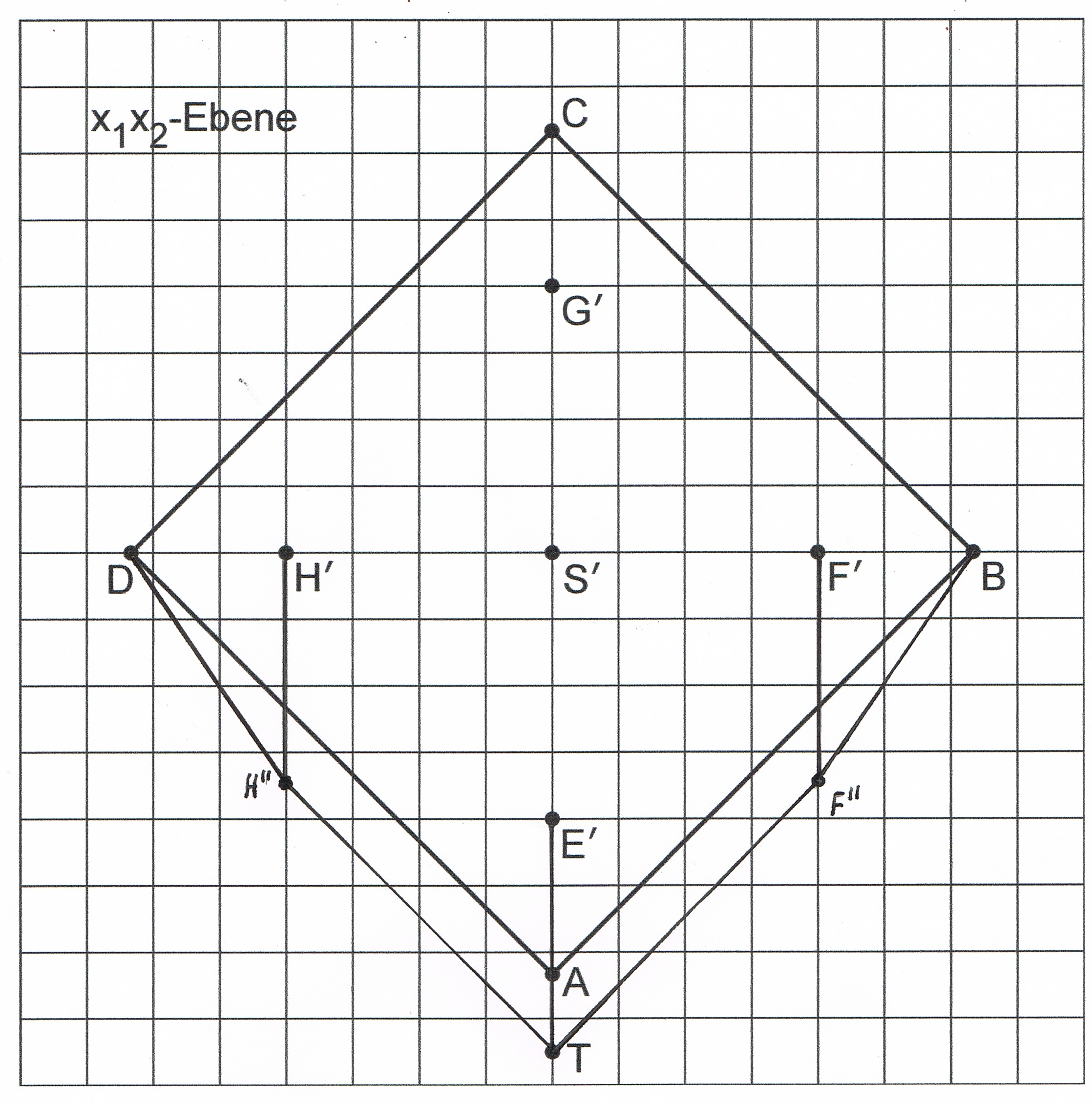
Zu einem bestimmten Zeitpunkt fallen auf die Knickpyramide Sonnenstrahlen, die im Modell durch parallele Geraden mit dem Richtungsvektor $\vec{S_{15} E}$ dargestellt werden. Der Schatten der Spitze der Knickpyramide auf dem horizontalen Boden wird durch den Punkt $T$ beschrieben. Die Lote durch die Punkte $E, F, G, H$ und $S_{15}$ auf die $x_{1} x_{2}$ -Ebene schneiden diese in den Punkten $E^{'}, F^{'}, G^{'}, H^{'}$ bzw. $S^{'} .$ Diese sind zusammen mit der Grundfläche der Pyramide und dem Punkt $T$ in Abbildung 3 dargestellt.
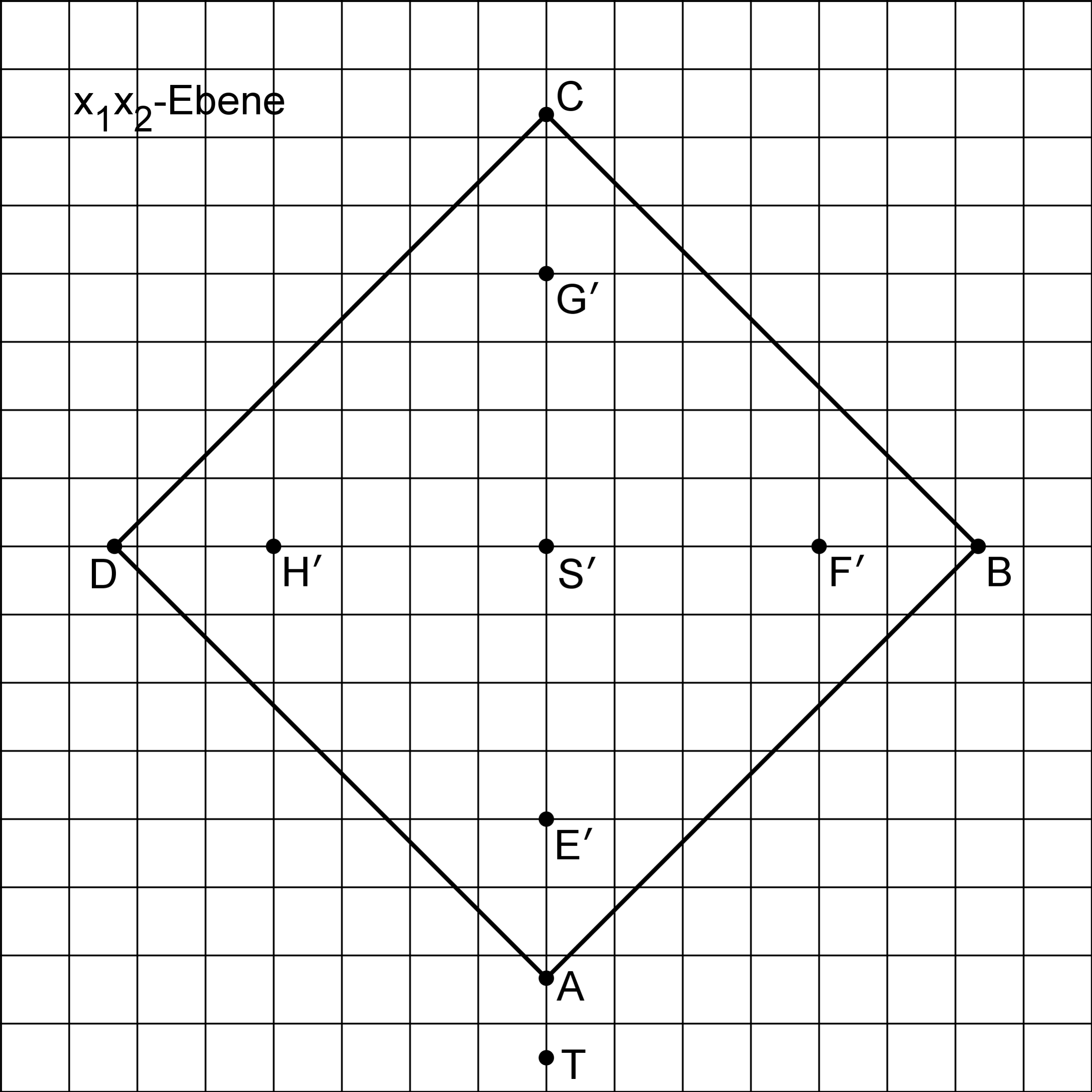
Abb. 3
Berechnen Sie die Koordinaten von $T$ . (3 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Die Sonnenstrahlen sind parallele Geraden mit dem Richtungsvektor $\vec{S_{15} E}$ .
Berechne den Richtungsvektor:
$\vec{S_{15} E} = \vec{E} - {\vec{S}}_{15} = (\begin{array}{c} 12 \\ 0 \\ 7 \end{array}) - (\begin{array}{c} 0 \\ 0 \\ 15 \end{array}) = (\begin{array}{c} 12 \\ 0 \\ - 8 \end{array})$
Erstelle die Geradengleichung für die Sonnenstrahlen, die durch den Punkt $S_{15}$ entlang von $E$ verläuft.
$g_{Licht} : \vec{X} = {\vec{S}}_{15} + r \cdot \vec{S_{15} E}$
Setze die Vektoren ein:
$g_{Licht} : \vec{X} = (\begin{array}{c} 0 \\ 0 \\ 15 \end{array}) + r \cdot (\begin{array}{c} 12 \\ 0 \\ - 8 \end{array})$
Den Schattenpunkt in der $x_{1} x_{2}$ -Ebene erhält man, indem $x_{3}$ in der Geradengleichung gleich null gesetzt wird.
$x_{3} = 0$
$0$ $=$ $15 - 8 r$ $+ 8 r$
$8 r$ $=$ $15$ $: 8$
$r$ $=$ $\frac{15}{8}$
Setze $r = \frac{15}{8}$ in die Geradengleichung ein, um die Koordinaten des Schattenpunktes $T$ zu erhalten.
${\vec{X}}_{T}$ $=$ $(\begin{array}{c} 0 \\ 0 \\ 15 \end{array}) + r \cdot (\begin{array}{c} 12 \\ 0 \\ - 8 \end{array})$
↓
Setze $r = \frac{15}{8}$ ein.
$=$ $(\begin{array}{c} 0 \\ 0 \\ 15 \end{array}) + \frac{15}{8} \cdot (\begin{array}{c} 12 \\ 0 \\ - 8 \end{array})$
↓
Fasse zusammen.
$=$ $(\begin{array}{c} 0 + \frac{15}{8} \cdot 12 \\ 0 + 0 \\ 15 + \frac{15}{8} \cdot (- 8) \end{array})$
↓
Vereinfache.
$=$ $(\begin{array}{c} 22,5 \\ 0 \\ 0 \end{array})$
Der Schattenpunkt $T$ hat die Koordinaten $T (22,5 | 0 | 0)$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
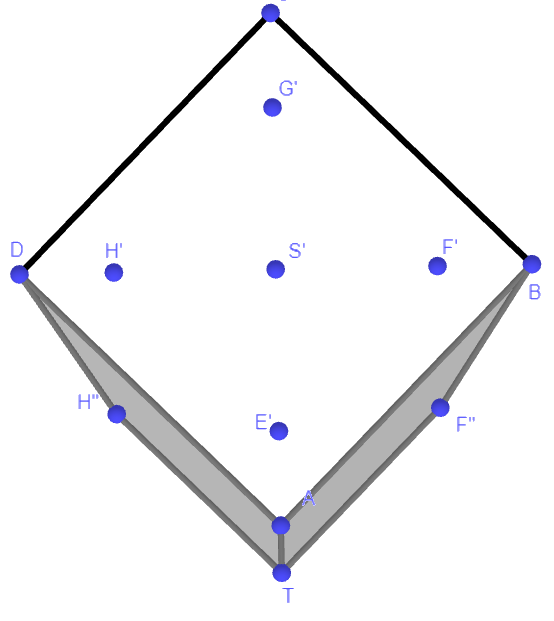
Der Schattenbereich der gesamten Pyramide auf dem Boden besteht im Modell aus zwei kongruenten Vierecken. Zeichnen Sie diesen Schattenbereich in Abbildung 3 ein und geben Sie die besondere Form der genannten Vierecke an. (4 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Trapez
Schattenbereich einzeichnen
Die Entfernung von $E^{'}$ zu $T$ sind $3,5$ Kästchen. Um den Schattenpunkt von $F^{'}$ zu bekommen, trägt man diese $3,5$ Kästchen in Punkt $F^{'}$ ab (gleiche Richtung wie die Strecke $[E^{'} T]$ , da das Licht parallel einfällt) und erhält den Punkt $F^{''}$ .
Entsprechend verfährt man mit dem Punkt $H^{'}$ und erhält den Schattenpunkt $H^{''}$ .
Der Punkt $B$ liegt in der $x_{1} x_{2}$ -Ebene. Hier beginnt der Schatten.
Verbinde nun die Punkte $B$ mit $F^{''}$ , $F^{''}$ mit $T$ , $T$ mit $A$ und $A$ wieder mit $B$ . Das eine Schattenviereck ist eingezeichnet.
Verfahre entsprechend auf der anderen Seite.
Eingezeichneter Schattenbereich
Besondere Form der Vierecke
Die Pyramidenkanten $[E F]$ und $[A B]$ sind parallel zueinander. Parallele Kanten werden parallel abgebildet. Somit ist auch die Schattengrenze $[T F^{''}]$ parallel dazu.
Die beiden Stecken $[T A]$ und $[F^{''} B]$ sind ungleich lang.
Ein Viereck mit zwei parallelen Seiten und zwei ungleich langen Seiten ist ein Trapez.
Das Viereck $A B F^{''} T$ ist also ein Trapez, ebenso das Viereck $A D H^{''} T$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das?

$L : (\vec{X} - \vec{A}) \circ \vec{n}$	$=$	$0$
	↓	Setze $\vec{A}$ und $\vec{n}$ ein.
$(\vec{X} - (\begin{array}{c} 19 \\ 0 \\ 0 \end{array})) \circ (\begin{array}{c} 1 \\ 1 \\ 1 \end{array})$	$=$	$0$

$((\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}) - (\begin{array}{c} 19 \\ 0 \\ 0 \end{array})) \circ (\begin{array}{c} 1 \\ 1 \\ 1 \end{array})$	$=$	$0$
	↓	Berechne das Skalarprodukt.
$x_{1} \cdot 1 + x_{2} \cdot 1 + x_{3} \cdot 1 - (19 \cdot 1 + 0 \cdot 1 + 0 \cdot 1)$	$=$	$0$
	↓	Fasse zusammen.
$x_{1} + x_{2} + x_{3} - 19$	$=$	$0$

$\cos (φ)$	$=$	$\frac{{\vec{n}}_{L} \circ {\vec{n}}_{x_{1} x_{2}}}{\| {\vec{n}}_{L} \| \cdot \| {\vec{n}}_{x_{1} x_{2}} \|}$
	↓	Setze die Vektoren und ihre Beträge ein.
	$=$	$\frac{(\begin{array}{c} 1 \\ 1 \\ 1 \end{array}) \circ (\begin{array}{c} 0 \\ 0 \\ 1 \end{array})}{\sqrt{3} \cdot 1}$
	↓	Berechne das Skalarprodukt.
	$=$	$\frac{1 \cdot 0 + 1 \cdot 0 + 1 \cdot 1}{\sqrt{3} \cdot 1}$
	↓	Vereinfache.
	$=$	$\frac{1}{\sqrt{3}}$

$φ$	$=$	$\cos^{- 1} (\frac{1}{\sqrt{3}})$
	$\approx$	${54,74}^{\circ}$

$0$	$=$	$15 - 8 r$	$+ 8 r$
$8 r$	$=$	$15$	$: 8$
$r$	$=$	$\frac{15}{8}$

${\vec{X}}_{T}$	$=$	$(\begin{array}{c} 0 \\ 0 \\ 15 \end{array}) + r \cdot (\begin{array}{c} 12 \\ 0 \\ - 8 \end{array})$
	↓	Setze $r = \frac{15}{8}$ ein.
	$=$	$(\begin{array}{c} 0 \\ 0 \\ 15 \end{array}) + \frac{15}{8} \cdot (\begin{array}{c} 12 \\ 0 \\ - 8 \end{array})$
	↓	Fasse zusammen.
	$=$	$(\begin{array}{c} 0 + \frac{15}{8} \cdot 12 \\ 0 + 0 \\ 15 + \frac{15}{8} \cdot (- 8) \end{array})$
	↓	Vereinfache.
	$=$	$(\begin{array}{c} 22,5 \\ 0 \\ 0 \end{array})$

Ist das Viereck ist ein Trapez?

Das Trapez hat zwei gleich lange Seiten

Hast du eine Frage oder Feedback?

Eine Gleichung von L in Koordinatenform

Berechnung der Größe φ des Winkels, den L mit der x1x2-Ebene einschließt

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Höhendifferenz

Im unteren Teil des Bauwerks ist der Neigungswinkel der Seitenflächen gegenüber dem Boden um mehr als 9∘ größer, als im oberen Teil des Bauwerks.

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Schattenbereich einzeichnen

Eingezeichneter Schattenbereich

Besondere Form der Vierecke

Hast du eine Frage oder Feedback?

Eine Gleichung von $L$ in Koordinatenform

Berechnung der Größe $φ$ des Winkels, den $L$ mit der $x_{1} x_{2}$ -Ebene einschließt

Im unteren Teil des Bauwerks ist der Neigungswinkel der Seitenflächen gegenüber dem Boden um mehr als $9^{\circ}$ größer, als im oberen Teil des Bauwerks.