Aufgaben zu den Extrempunkten

Hier findest du Aufgaben zu Hoch- und Tiefpunkten. Vertiefe dein Wissen mit Zuordnungs- und Rechenaufgaben.

1
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremum
Richtige Lösung
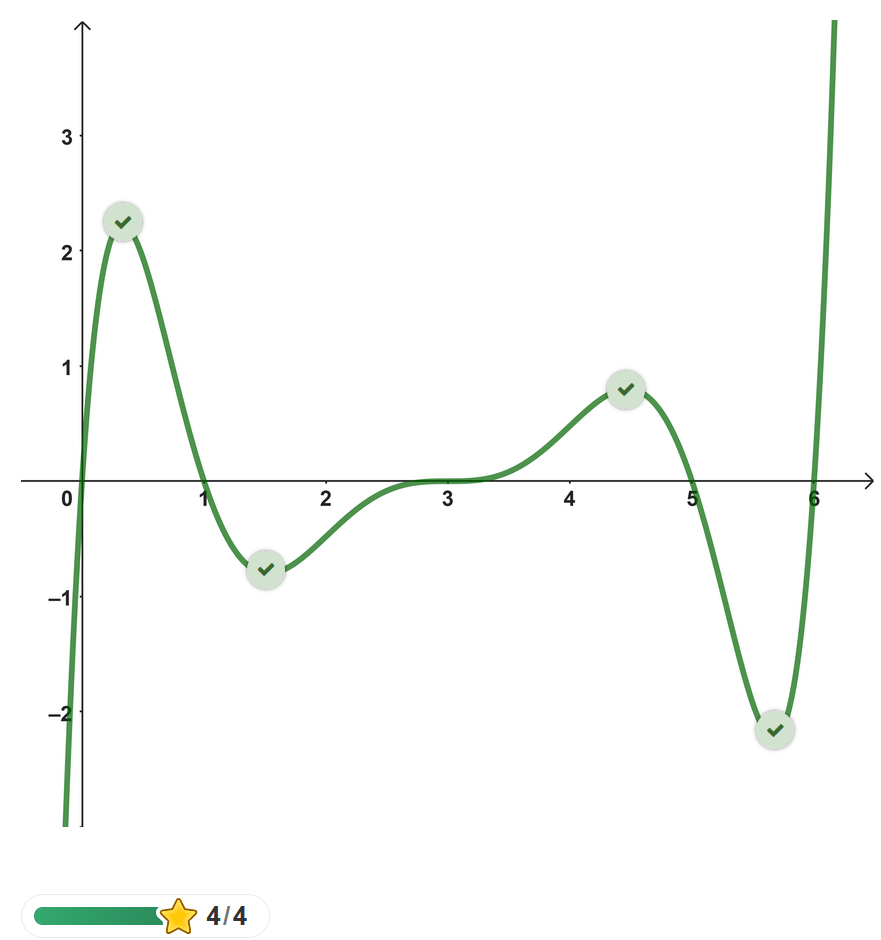
Lokale Extrempunkte sind $Hochpunkte$ und $Tiefpunkte$ .
Es sind ein paar Fallen eingebaut:
Nullstellen sind im Allgemeinen keine Extrempunkte, außer sie sind eben gleichzeitig Hochpunkte oder Tiefpunkte.
Wendepunkte sind ebenfalls keine Extrempunkte
Sattelpunkte sind spezielle Wendepunkte, aber keine Extrempunkte
2
Bestimme rechnerisch die lokalen Extrema der Funktion mit der Gleichung:
$f (x) = x^{3} + x^{2} - x + 1$

Bilde die ersten beiden Ableitungen:
$f^{'} (x) = 3 x^{2} + 2 x - 1$
$f^{''} (x) = 6 x + 2$
Damit ein lokales Extremum existiert, muss die notwendige Bedingung $f^{'} (x) = 0$ erfüllt sein:
$f^{'} (x) = 0$
$3 x^{2} + 2 x - 1 = 0$
$x^{2} + \frac{2}{3} x - \frac{1}{3} = 0$
$x_{1} = - \frac{1}{3} + \sqrt{(\frac{1}{3})^{2} + \frac{1}{3}} = - \frac{1}{3} + \sqrt{\frac{1}{9} + \frac{3}{9}} = \frac{1}{3}$
$x_{2} = - \frac{1}{3} - \sqrt{(\frac{1}{3})^{2} + \frac{1}{3}} = - \frac{1}{3} - \sqrt{\frac{1}{9} + \frac{3}{9}} = - 1$
Damit gibt es zwei Kandidaten für lokale Extrema. Falls die zweite Ableitung bei einem gefundenen Kandidaten ungleich Null ist, ist die hinreichende Bedingung erfüllt und es ist nachgewiesen, dass es sich um lokale Extremstellen handelt:
$f^{''} (\frac{1}{3}) = 6 \cdot \frac{1}{3} + 2 = 4$
Das ist echt größer als Null. Damit ist $x_{1} = \frac{1}{3}$ eine lokale Extremstelle. Da die zweite Ableitung größer Null ist, muss hier ein Minimum vorliegen. Um den Extrempunkt angeben zu können muss man nun noch $x_{1} = \frac{1}{3}$ in die Funktionsgleichung einsetzen:
$f (\frac{1}{3}) = {(\frac{1}{3})}^{3} + {(\frac{1}{3})}^{2} - \frac{1}{3} + 1 = \frac{22^{}}{27}$
Also ist ein lokales Mininmum gefunden: $M i n (\frac{1}{3}; \frac{22}{27})$
Nun noch für $x_{2} = - 2$ das gleiche Vorgehen:
$f^{''} (- 1) = 6 \cdot (- 1) + 2 = - 4$
Das ist echt kleiner als Null. Damit ist $x_{2} = - 1$ eine lokale Extremstelle. Da die zweite Ableitung kleiner Null ist, muss hier ein Maximum vorliegen. Um den Extrempunkt angeben zu können muss man nun noch $x_{2} = - 1$ in die Funktionsgleichung einsetzen:
$f (- 1) = {(- 1)}^{3} + {(- 1)}^{2} - (- 1) + 1 = 2$
Also ist ein lokales Maximum gefunden: $M a x (- 1; 2)$
3
Untersuche die gegebenen Funktionen auf lokale Extrema!
1. $f (x) = x^{2} + 3$
  
  Wir benötigen die ersten beiden Ableitungen:
  $\begin{array}{l} f^{'} (x) = 2 x \\ f^{''} (x) = 2 \end{array}$
  Damit ein lokales Extremum vorliegt, muss die erste Ableitung Null sein.
  $\begin{array}{l} 0 = 2 x \\ x_{E} = 0 \end{array}$
  Damit haben wir einen Kandidaten. Wenn nun noch die zweite Ableitung ungleich Null ist, haben wir ein Extremum gefunden. Wenn die zweite Ableitung gleich Null ist kann es immer noch ein Extremum sein. Wir benötigen dann das Vorzeichenwechselkriterium.
  $f^{''} (0) = 2 > 0$
  Die zweite Ableitung ist größer Null, es muss also ein Minimum vorliegen.
  Für das Minimum benötigen wir noch den y-Wert. Dazu setzen wir den gefundenen x-Wert in die Funktionsgleichung ein:
  $f (0) = 0^{2} + 3 = 3$
  Bei $Min (0 | 3)$ liegt ein lokales Minimum vor.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $f (x) = x^{4} - 2$
  
  Wir benötigen die ersten beiden Ableitungen:
  $\begin{array}{l} f^{'} (x) = 4 x^{3} \\ f^{''} (x) = 12 x^{2} \end{array}$
  Damit ein lokales Extremum vorliegt, muss die erste Ableitung Null sein.
  $\begin{array}{l} 0 = 4 x^{3} \\ x_{E} = 0 \end{array}$
  Damit haben wir einen Kandidaten. Wenn nun noch die zweite Ableitung ungleich Null ist, haben wir ein Extremum gefunden. Wenn die zweite Ableitung gleich Null ist kann es immer noch ein Extremum sein. Wir benötigen dann das Vorzeichenwechselkriterium.
  $f^{''} (0) = 12 \cdot 0^{2} = 0$
  Die zweite Ableitung ist gleich Null. Wir müssen mit dem Vorzeichenwechselkriterium weiter arbeiten. Dazu betrachten wir die erste Ableitung von f. Sie ist eine Funktion dritten Grades, welche bei Null das Vorzeichen vom Negativen zum Positiven wechselt. Die Funktion f geht also vom Fallen ins Steigen über. Es liegt also ein Minimum vor.
  Für das Minimum benötigen wir noch den y-Wert. Dazu setzen wir den gefundenen x-Wert in die Funktionsgleichung ein:
  $f (0) = 0^{2} - 2 = - 2$
  Bei $Min (0 | - 2)$ liegt ein lokales Minimum vor.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $f (x) = x^{3} - x^{2} - x - 1$
  
  Wir benötigen die ersten beiden Ableitungen:
  $\begin{array}{l} f^{'} (x) = 3 x^{2} - 2 x - 1 \\ f^{''} (x) = 6 x - 2 \end{array}$
  Damit ein lokales Extremum vorliegt, muss die erste Ableitung Null sein.
  $\begin{array}{l} 0 = 3 x^{2} - 2 x - 1 \\ x_{1} = 1 \\ x_{2} = - \frac{1}{3} \end{array}$
  Damit haben wir zwei Kandidaten. Wenn nun noch die zweite Ableitung ungleich Null ist, haben wir ein Extremum gefunden. Wenn die zweite Ableitung gleich Null ist kann es immer noch ein Extremum sein. Wir benötigen dann das Vorzeichenwechselkriterium.
  Für $x_{1} = 1$ :
  $f^{''} (1) = 6 \cdot 1 - 2 = 4 > 0$
  Die zweite Ableitung ist größer Null, es muss also ein Minimum vorliegen.
  Für das Minimum benötigen wir noch den y-Wert. Dazu setzen wir den gefundenen x-Wert in die Funktionsgleichung ein:
  $f (1) = 1^{3} - 1^{2} - 1 - 1 = - 2$
  Bei $Min (1 | - 2)$ liegt ein lokales Minimum vor.
  Für $x_{2} = - \frac{1}{3}$ :
  $f^{''} (- \frac{1}{3}) = 6 \cdot (- \frac{1}{3}) - 2 = - 4 < 0$
  Die zweite Ableitung ist kleiner Null, es muss also ein Maximum vorliegen.
  Für das Maximum benötigen wir noch den y-Wert. Dazu setzen wir den gefundenen x-Wert in die Funktionsgleichung ein:
  $f (- \frac{1}{3}) = (- \frac{1}{3})^{3} - (- \frac{1}{3})^{2} - (- \frac{1}{3}) - 1 = - \frac{22}{27}$
  Bei $Max (- \frac{1}{3} | - \frac{22}{27})$ liegt ein lokales Maximum vor.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. $f (x) = e^{x} - 3 x$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen
  Wir benötigen die ersten beiden Ableitungen:
  $\begin{array}{l} f^{'} (x) = e^{x} - 3 \\ f^{''} (x) = e^{x} \end{array}$
  Damit ein lokales Extremum vorliegt, muss die erste Ableitung Null sein.
  $\begin{array}{l} 0 = e^{x} - 3 \\ x_{E} = \ln (3) \approx 1.0986 \end{array}$
  Damit haben wir einen Kandidaten. Wenn nun noch die zweite Ableitung ungleich Null ist, haben wir ein Extremum gefunden. Wenn die zweite Ableitung gleich Null ist kann es immer noch ein Extremum sein. Wir benötigen dann das Vorzeichenwechselkriterium.
  $f^{''} (\ln (3)) = e^{\ln (3)} = 3 > 0$ Die zweite Ableitung ist größer Null, es muss also ein Minimum vorliegen.
  Für das Minimum benötigen wir noch den y-Wert. Dazu setzen wir den gefundenen x-Wert in die Funktionsgleichung ein:
  $f (\ln (3)) = e^{\ln (3)} - 3 \cdot \ln (3) = 3 - 3 \cdot \ln (3) \approx - 0.2958$
  Bei $Min (1.0986 | - 0.29583)$ liegt ein lokales Minimum vor.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5. $f (x) = 8 x^{3} + 4$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen
  Wir benötigen die ersten beiden Ableitungen:
  $\begin{array}{l} f^{'} (x) = 24 x^{2} \\ f^{''} (x) = 48 x \end{array}$
  Damit ein lokales Extremum vorliegt, muss die erste Ableitung Null sein.
  $\begin{array}{l} 0 = 24 x^{2} \\ x_{E} = 0 \end{array}$
  Damit haben wir einen Kandidaten. Wenn nun noch die zweite Ableitung ungleich Null ist, haben wir ein Extremum gefunden. Wenn die zweite Ableitung gleich Null ist kann es immer noch ein Extremum sein. Wir benötigen dann das Vorzeichenwechselkriterium.
  $ f^{''} (0) = 48 \cdot 0 = 0$
  Die zweite Ableitung ist gleich Null. Wir müssen mit dem Vorzeichenwechselkriterium weiter arbeiten. Dazu betrachten wir die erste Ableitung von $f$ . Sie ist eine Funktion zweiten Grades, welche bei Null ein lokales Minimum hat. Sie wechselt das Vorzeichen nicht. Es liegt kein lokales Extremum vor.
  Die Funktion $f$ ist also links von $x = 0$ monoton steigend, bei $x = 0$ waagerecht und rechts von $x = 0$ wieder monoton steigend. Es liegt ein Terrassenpunkt (auch Sattelpunkt oder Horizontalwendepunkt) vor.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4
Gegeben ist die Funktion mit der Gleichung $f (x) = x^{4} - x^{3} - x^{2}$ .
Bestimme die lokalen Extrema.
Bei der Lösung einer quadratischen Gleichung und bei den Funktionswerten kannst du einen Rechner verwenden.

Wir benötigen die ersten beiden Ableitungen:
$f^{'} (x) = 4 x^{3} - 3 x^{2} - 2 x$
$f^{''} (x) = 12 x^{2} - 6 x - 2$
Damit ein lokales Extremum vorliegt, muss die erste Ableitung Null sein.
$0 = 4 x^{3} - 3 x^{2} - 2 x$
Klammert man hier x aus, bekommt man drei Kandidaten:
$0 = x (4 x^{2} - 3 x - 2)$
$x_{1} = - 0.4254$
$x_{2} \approx 0$
$x_{3} \approx 1.1754$
Damit haben wir drei Kandidaten. Wenn nun noch die zweite Ableitung ungleich Null ist, haben wir ein Extremum gefunden. Wenn die zweite Ableitung gleich Null ist, kann es immer noch ein Extremum sein. Wir benötigen dann das Vorzeichenwechselkriterium.
$f^{''} (- 0.4254) = 2.7240 > 0$
Die zweite Ableitung ist größer Null, es muss also ein Minimum vorliegen.
$f^{''} (0) \approx - 2 < 0$
Die zweite Ableitung ist kleiner Null, es muss also ein Maximum vorliegen.
$f^{''} (1.1754) \approx 7.5262 > 0$
Die zweite Ableitung ist größer Null, es muss also ein Minimum vorliegen.
Für die Extrema benötigen wir noch die y-Werte. Dazu setzen wir die gefundenen x-Werte in die Funktionsgleichung ein:
$f (- 0.4254) \approx - 0.0712$
$f (0) = 0$
$f (1.1754) \approx - 1.0967$
Die Funktion hat drei Extrema:
${Min}_{1} (- 0.4254 | - 0.0712)$
$Max (0 | 0)$
${Min}_{2} (1.1754 | - 1.0967)$
Bilde die ersten beiden Ableitungen und suche die Nullstellen der ersten.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Aufgaben zu den Extrempunkten

Richtige Lösung

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?