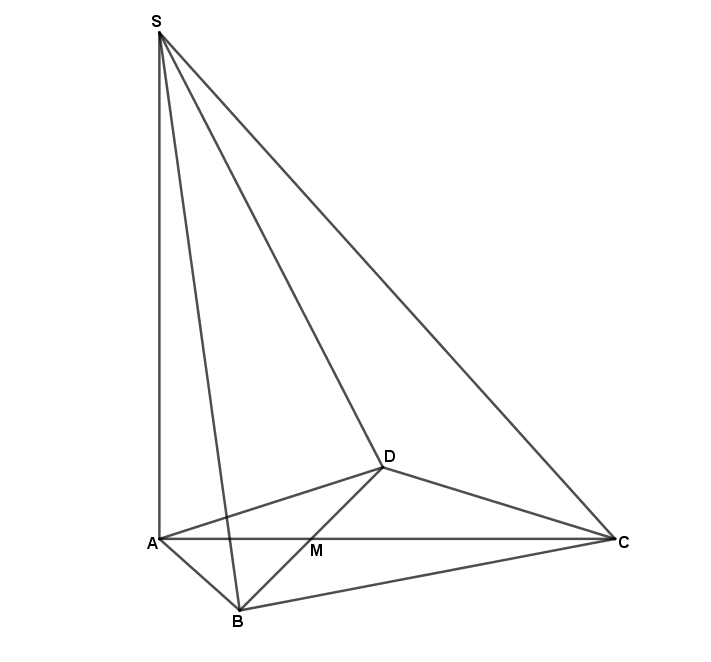
Die Skizze unten zeigt ein Schrägbild der Pyramide mit der Höhe , deren Grundfläche das Drachenviereck mit dem Diagonalenschnittpunkt ist.
Es gilt: .
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
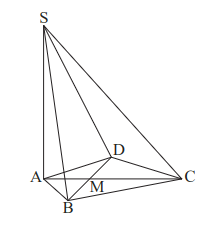
Zeichnen Sie das Schrägbild der Pyramide , wobei die Strecke auf der Schrägbildachse und der Punkt links vom Punkt liegen soll.
Für die Zeichnung gilt:
Links vom Punkt sind freizuhalten.
Berechnen Sie sodann die Länge der Strecke und das Maß des Winkels .
Ergebnisse:
Für diese Aufgabe benötigst du folgendes Grundwissen: Satz des Pythagoras und Sinus, Kosinus und Tangens
Schrägbild der Pyramide
Das Applet hilft dir dabei das Schrägbild der Pyramide Schritt für Schritt zu zeichnen.
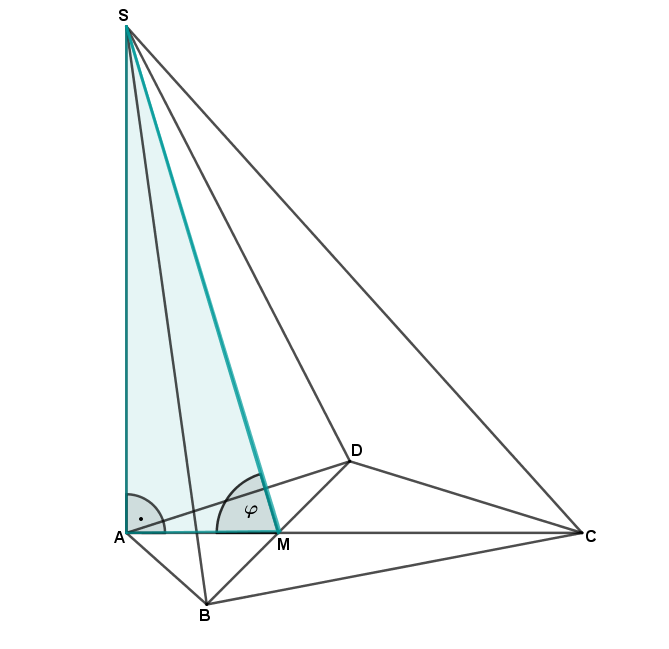
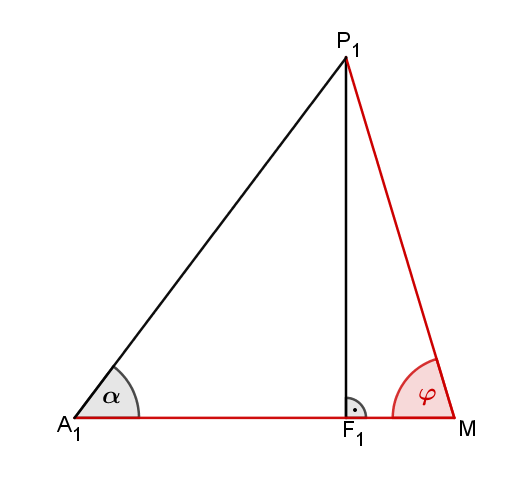
Zur Berechnung der Länge der Strecke und des Maß des Winkels benötigst du ein passendes Dreieck in deiner Pyramide, das deine gesuchten Größen enthält. Hierfür verwendest du das rechtwinklige Dreieck , welches in der untenstehenden Abbildung eingezeichnet ist.
Berechnung der Länge der Strecke
Das oben eingezeichnete Dreieck ist rechtwinklig. Du hast auch bereits und gegeben, sodass du die Länge der Strecke erhältst, indem du den Satz des Pythagoras anwendest. Die Strecke ist die Hypotenuse und die Strecken und sind die beiden Katheten.
Jetzt muss du noch die Wurzel ziehen, um die Länge von zu erhalten, wobei du nur die positive Lösung berücksichtigst, da eine negative Länge keinen Sinn macht:
Berechnung des Maß des Winkels
Bei der Bestimmung des Winkelmaßes hilft dir wieder die obige Zeichnung. In einem rechtwinkligen Dreieck hast du die Möglichkeit, das Maß eines Winkels mittels Sinus, Kosinus und Tangens zu berechnen. In dem betrachteten Dreieck kannst du alle drei trigonometrischen Funktionen anwenden, da du alle Seitenmaße gegeben hast. Zur Berechnung wird hier der Tangens verwendet:
Diese Formel löst du nun nach auf, wobei du die Umkehrfunktion des Tangens verwendest:
Du setzt jetzt noch die gegebenen Maße ein:
Die Länge der Strecke beträgt und das Maß des Winkels ist .
Hast du eine Frage oder Feedback?
Für Punkte auf der Strecke gilt: ( und ).
Verlängert man die Diagonale über den Punkt hinaus um , so erhält man Punkte und es entstehen neue Pyramiden .
Zeichnen Sie die Pyramide und die zugehörige Höhe mit dem Höhenfußpunkt für in das Schrägbild zu Teilaufgabe a) ein.
Pyramide und Höhe
Die Angabe dieser Teilaufgabe liefert dir die folgenden Informationen:
Punkte auf der Strecke :
Verlängerung der Diagonalen über den Punkt hinaus, sodass man erhält:
Höhenfußpunkt
Die Größen, die du zum Zeichnen der Pyramide benötigst, erhältst du für :
Du kannst die Pyramide nun wie folgt einzeichnen:
Einzeichnen von : Du verlängerst die Diagonale über den Punkt hinaus um , sodass du den Punkt erhältst.
Einzeichnen des Punktes : Mit dem Lineal: Du misst vom Punkt ausgehend auf der Strecke ab und zeichnest dort den Punkt ein. Mit dem Zirkel: Stelle deinen Zirkel auf ein. Stich mit deinem Zirkel bei Punkt ein und trage auf der Strecke ab. Zeichne an diese Stelle den Punkt ein.
Einzeichnen der fehlenden Strecken: Zeichnen nun die Strecken , , , , und ein.
Einzeichnen der Höhe mit dem Höhenfußpunkt : Die Höhe steht senkrecht auf der Grundfläche der Pyramide . Der Höhenfußpunkt liegt auf der Diagonalen . Um die Höhe zu erhalten, zeichnest du das Lot vom Punkt auf die Strecke . Der Schnittpunkt des Lotes mit ist der Höhenfußpunkt .
Hast du eine Frage oder Feedback?
Berechnen Sie das Maß des Winkels .
Für diese Aufgabe benötigst du folgendes Grundwissen: Sinussatz und Kosinussatz
Berechnen des Maß des Winkels
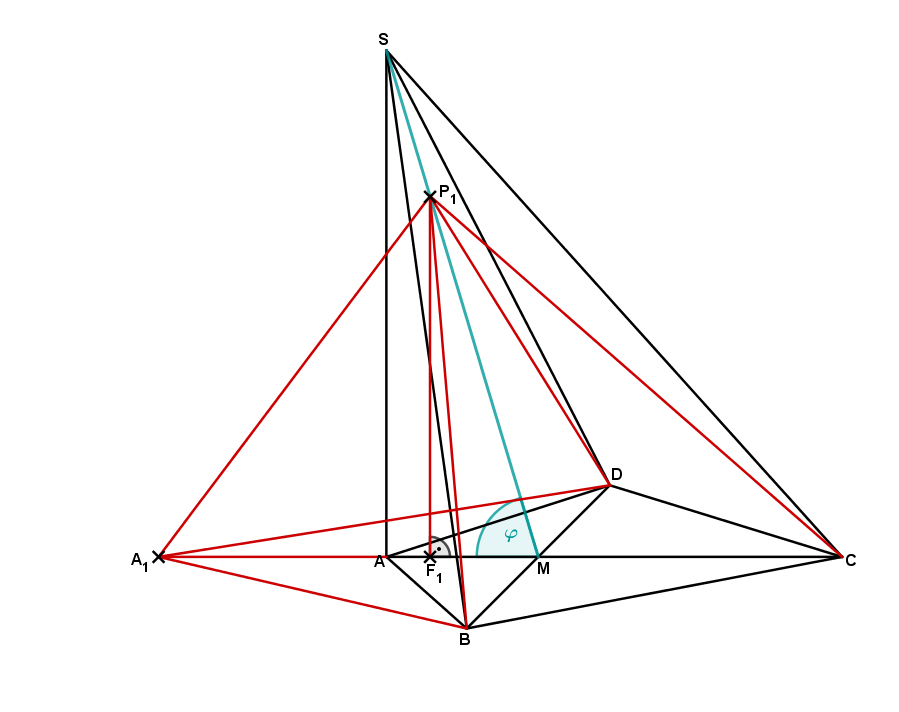
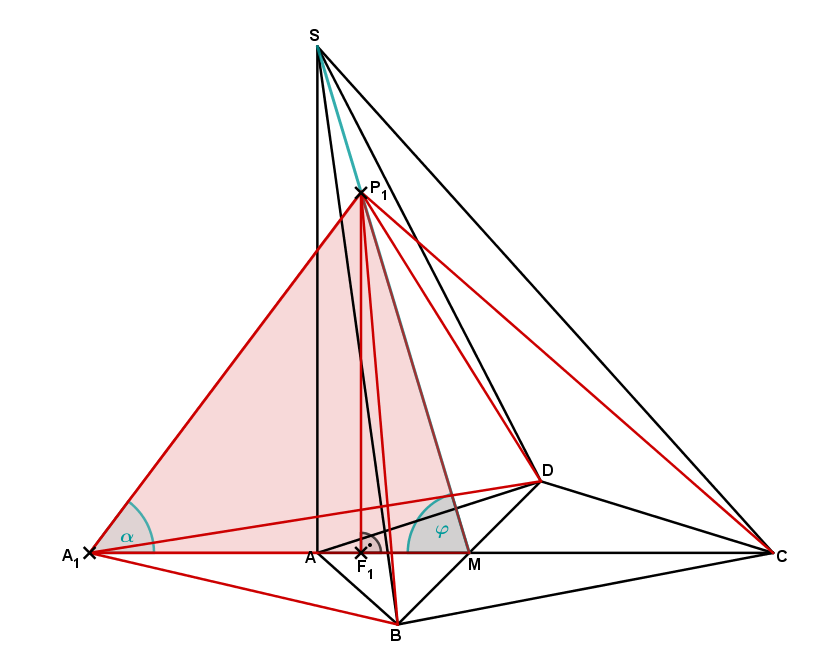
In der vorherigen Teilaufgabe hast du die Pyramide zu der ursprünglichen Pyramide eingezeichnet. Zur Berechnung des Maß des Winkels musst du dir wieder ein passendes Dreieck in der Pyramide suchen, welches diesen Winkel enthält. Hierfür bietet sich das Dreieck an, das in der folgenden Abbildung eingezeichnet ist.
Bei dem Dreieck handelt es sich um ein allgemeines Dreieck, in dem du bereits das Maß gegeben hast. Das Winkelmaß kannst du mithilfe des Sinussatzes berechnen:
In dieser Formel fehlen dir jedoch noch die Längen der Strecken und , die du dir aber aus den gegebenen Größen berechnen kannst.
Du kannst nun wie folgt vorgehen, um das Winkelmaß zu bestimmen:
Berechne die Länge der Seite .
Berechne die Länge der Seite .
Berechne die Länge der Seite .
Berechne das Winkelmaß .
1. Berechnung der Länge der Seite
In Teilaufgabe a) hast du die Länge der Strecke berechnet und aus Teilaufgabe b) hast du die Information, dass lang ist. Mithilfe dieser Größen kannst du die Länge der Seite bestimmen, indem du von die Strecke abziehst:
2. Berechnung der Länge der Seite
Zur Berechnung der Länge der Seite benötigst du die in Teilaufgabe b) angegebene Größe für die Verlängerung der Diagonalen über den Punkt hinaus um . Für ergibt sich für die Verlängerung . Um zu erhalten, musst du noch die Längen von und addieren:
Im nebenstehenden Dreieck sind nun die bekannten Größen rot eingezeichnet.
3. Berechnung der Länge der Seite
Du benötigst noch die Länge der Seite . Diese kannst du mittels deiner bereits berechneten Größen und dem Kosinussatz im allgemeinen Dreieck ermitteln:
Nun ziehst du die Wurzel und setzt die gegebenen Größen ein, um zu erhalten. Du berücksichtigst hier nur die positive Lösung, da eine negative Länge keinen Sinn macht:
4. Berechnung des Winkelmaß
Somit hast du nun alle Werte gegeben, um das Winkelmaß mithilfe des Sinussatzes zu bestimmen:
Diese Formel stellst du nach um, indem du zuerst nach auflöst und dann die Umkehrfunktion des Sinus anwendest. Danach setzt du noch die Werte ein:
Das Maß des Winkels beträgt .
Hast du eine Frage oder Feedback?
Zeigen Sie rechnerisch, dass für das Volumen der Pyramiden in Abhängigkeit von gilt:
Teilergebnis:
Für diese Aufgabe benötigst du folgendes Grundwissen: Volumen Pyramide, Flächeninhalt Drachenviereck
Volumen der Pyramiden
Zunächst überlegst du dir, wie die Formel zur Berechnung des Volumens einer Pyramide aufgebaut ist. Im nächsten Schritt schreibst du dann deine Größen in Abhängigkeit von .
Allgemein gilt für das Volumen einer Pyramide:
wobei für die Grundfläche und für die Höhe der Pyramide stehen.
Im Folgenden gehst du nun wie folgt vor, um das Volumen der Pyramiden in Abhängigkeit von zu berechnen:
Bestimme die Grundfläche der Pyramiden in Abhängigkeit von
Berechne die Höhe der Pyramiden in Abhängigkeit von .
Berechne das Volumen der Pyramiden .
1. Bestimmen der Grundfläche der Pyramiden
Die Pyramiden besitzen als Grundfläche das Drachenviereck . Dieses ändert sich, wenn man, wie in der Angabe von Teilaufgabe b) beschrieben, die Diagonale verlängert.
Du überlegst dir nun zunächst, von welchen Größen der Flächeninhalt eines Drachenvierecks abhängt und stellst diese dann in Abhängigkeit von dar.
Der Flächeninhalt eines Drachenvierecks lässt sich allgemein darstellen durch:
wobei und für die Diagonalen des Drachenvierecks stehen.
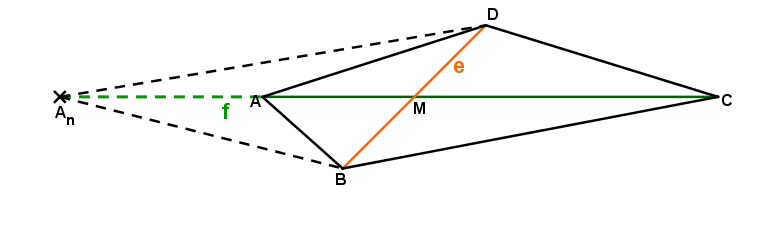
In der folgenden Skizze wird die Grundfläche der Pyramiden beispielhaft dargestellt, wobei die Diagonalen und eingezeichnet sind und variabel ist.
Bestimmen der Diagonalen des Drachenvierecks
Die Diagonale entspricht in der Zeichnung der Strecke und ändert sich nicht bei der Verlängerung der Diagonalen . Anders ist es bei der Diagonalen , die sich mit der Verlängerung der Diagonalen ändert und somit von abhängt. Sie entspricht der Strecke von .
Du schreibst jetzt die Diagonale in Abhängigkeit von . Die Länge der Strecke bleibt dabei unverändert. Du musst noch die Verlängerung von über hinaus berücksichtigen, welche ist. Du addierst nun die Längen und , um die Diagonale in Abhängigkeit von zu erhalten:
Bestimmen des Flächeninhalts des Drachenvierecks bzw. der Grundfläche
Du setzt nun deine beiden Diagonalen in die oben angegebene Formel für den Flächeninhalt des Drachenvierecks ein, und erhältst somit die Grundfläche der Pyramiden in Abhängigkeit von .
2. Bestimmen der Höhe der Pyramiden
Die Höhe der Pyramiden ist durch die Strecke gegeben. Diese ändert sich mit , da und von abhängen.
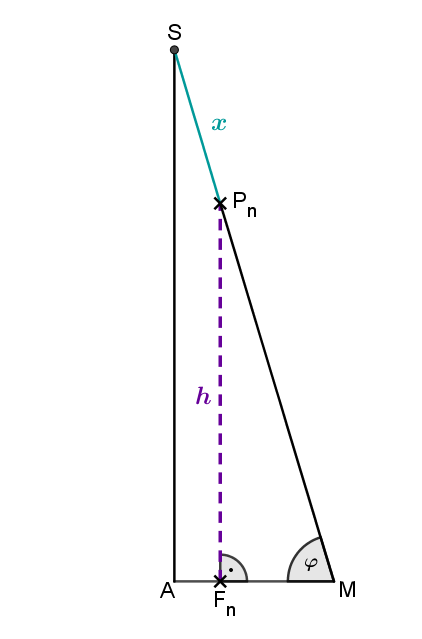
In der nebenstehenden Skizze ist die Höhe der Pyramiden stellvertretend in das Dreieck eingezeichnet.
Du hast im Dreieck bereits folgende Größen gegeben:
Winkelmaß
Länge der Strecke :
Punkte auf der Strecke :
Du musst nun die Höhe der Pyramiden in Abhängigkeit von darstellen. Diese bestimmst du, indem du das rechtwinklige Dreieck betrachtest. Die Höhe kannst du mithilfe des Sinus berechnen:
Bestimmen der Seite in Abhängigkeit von
Du benötigst noch die Länge der Seite , die du aus den gegebenen Größen berechnen kannst. Dazu subtrahierst du von die Strecke :
Berechnen der Höhe in Abhängigkeit von
Du hast nun alle Größen gegeben, um mit der oben dargestellten Formel die Höhe zu berechnen. Dazu löst du diese nach auf und setzt die Werte ein:
3. Berechnen des Volumens der Pyramiden
Um das Volumen zu berechnen, musst du nun in die Formel für das Volumen einer Pyramide die berechneten Größen einsetzten und ausmultiplizieren:
Das Volumen der Pyramiden in Abhängigkeit von beträgt .
Hast du eine Frage oder Feedback?
Unter den Pyramiden hat die Pyramide das maximale Volumen . Berechnen Sie, um wie viel Prozent größer als das Volumen der ursprünglichen Pyramide ist.
Für diese Aufgabe benötigst du folgendes Grundwissen: allgemeine Form und Scheitelform einer quadratischen Funktion, quadratische Ergänzung
Berechnen, um wie viel Prozent größer als ist
1. Berechnen des Volumens der ursprünglichen Pyramide
Zur Berechnung des Volumens kannst du die in Teilaufgabe d) berechnete Formel für das Volumen in Abhängigkeit von verwenden. Du setzt , da du bei der ursprünglichen Pyramide noch keine Verlängerung hast. Damit ergibt sich:
2. Berechnen des maximalen Volumens der Pyramiden
Die in Teilaufgabe d) berechnete Formel für das Volumen in Abhängigkeit von , , ist eine quadratische Funktion, welche eine nach unten geöffnete Parabel (negativer Wert vor ) darstellt. Diese besitzt ein Maximum, welches auch der Scheitelpunkt der Parabel ist. Um den Scheitelpunkt der Parabel zu bestimmen, musst du die allgemeine Form der quadratischen Funktion in die Scheitelform umwandeln. An dieser kannst du dann direkt den Scheitelpunkt ablesen. Mithilfe der quadratischen Ergänzung kannst du die beiden Formen ineinander umwandeln:
Du hast die Scheitelform der quadratischen Funktion bestimmt, sodass du nun direkt den Scheitelpunkt ablesen kannst. Dieser ist:
Der Wert des Scheitelpunkts gibt dir das maximale Volumen an.
Du berechnest jetzt noch, um wie viel Prozent größer als ist. Dazu teilst du die beiden Volumina durcheinander, um deren Verhältnis zu bestimmen:
Das Volumen ist um größer als das Volumen der Pyramide .
Hast du eine Frage oder Feedback?
Berechne das Volumen der ursprünglichen Pyramide.
Berechne das maximale Volumen der Pyramide .
Berechne das Verhältnis von zu .
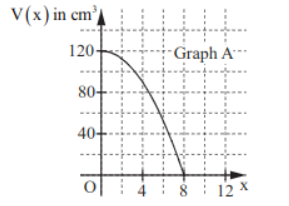
Zwei der folgenden Graphen stellen nicht das Volumen der Pyramiden in Abhängigkeit von dar. Geben Sie diese an und begründen Sie Ihre Entscheidung.
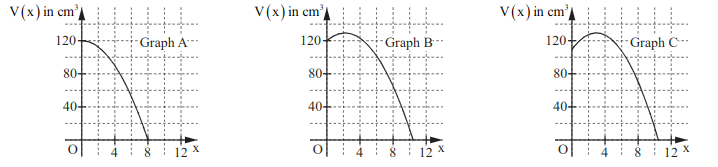
Graph A: falsch
Begründung: Das maximale Volumen liegt im Graphen bei . In Teilaufgabe e) hast du aber berechnet, dass das maximale Volumen ist und bei liegt, was im Graph nicht der Fall ist. Somit kann der Graph nicht das Volumen der Pyramiden darstellen.
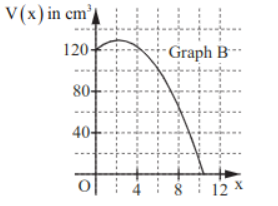
Graph B: richtig
Begründung: Das Volumen der ursprünglichen Pyramide , d.h. für , liegt im Graphen B bei . Ebenso stimmt in diesem Graph die Lage des maximalen Volumens mit dem in Teilaufgabe e) berechneten Werten überein, sodass dieser das Volumen der Pyramiden darstellt.
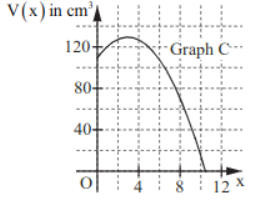
Graph C: falsch
Begründung: Das Volumen der ursprünglichen Pyramide , d.h. für , liegt im Graphen nicht bei , sondern ist . Somit kann der Graph nicht das Volumen der Pyramiden darstellen.
Hast du eine Frage oder Feedback?