Teil B - lernen mit Serlo!

Punkte $B_{n} (x | - 0,3 x - 1)$ liegen auf der Geraden $g$ mit der Gleichung $y = - 0,3 x - 1$ mit $𝔾 = ℝ \times ℝ$ . Sie sind zusammen mit dem Punkt $A (0 | 0)$ sowie Punkten $C_{n}$ und $D_{n}$ für $x > 0,84$ Eckpunkte von Drachenvierecken $A B_{n} C_{n} D_{n}$ mit den Diagonalenschnittpunkten $M_{n}$ .

Die Diagonalen $[A C_{n}]$ der Drachenvierecke $A B_{n} C_{n} D_{n}$ liegen auf der Symmetrieachse $h$ mit der Gleichung $y = \frac{2}{3} x (𝔾 = ℝ \times ℝ)$ . Es gilt: $\vec{A C_{n}} = 4 \cdot \vec{A M_{n}}$ .

Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

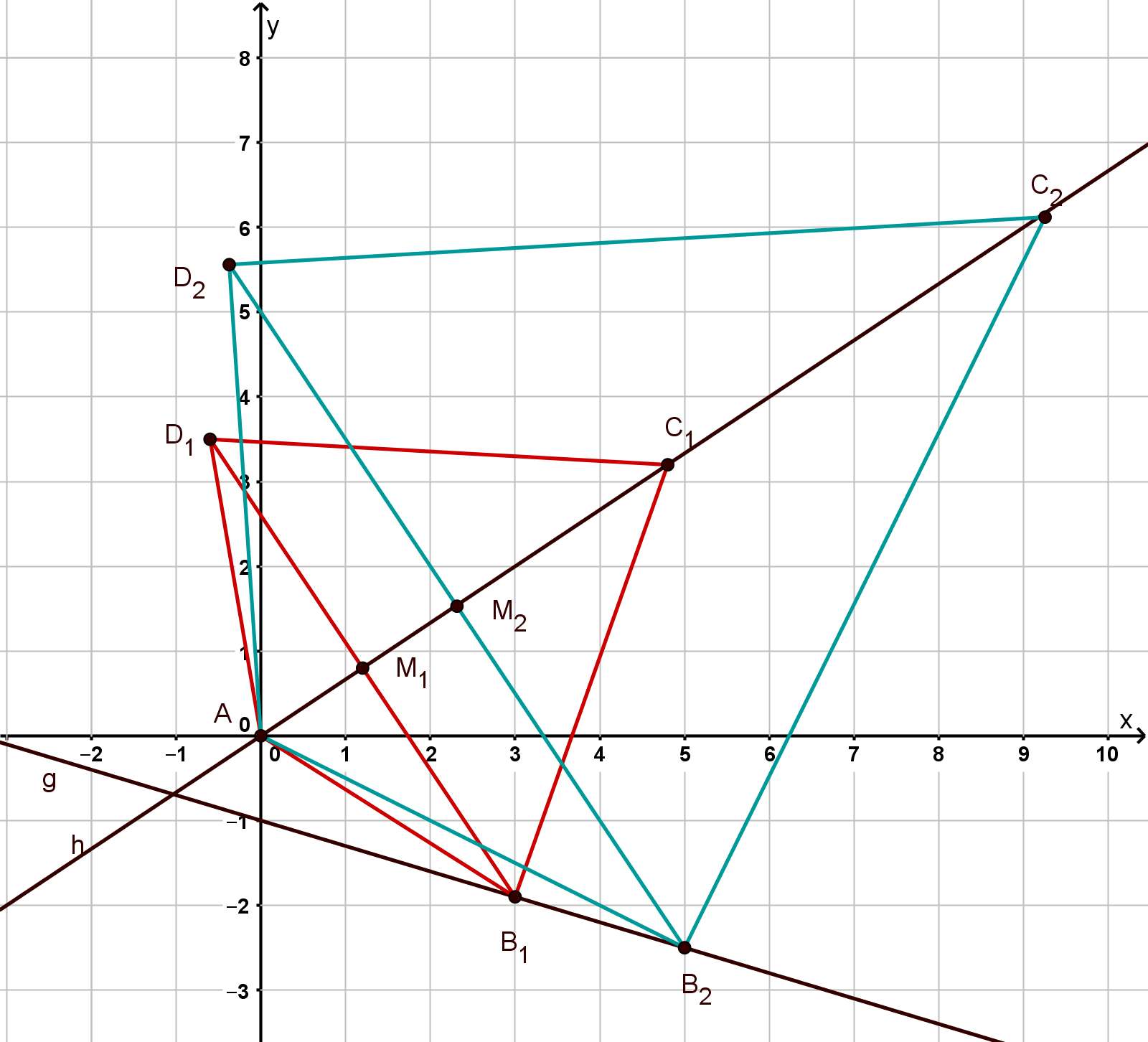
Zeichnen Sie die Geraden $g$ und $h$ sowie die Drachenvierecke $A B_{1} C_{1} D_{1}$ für $x = 3$ und $A B_{2} C_{2} D_{2}$ für $x = 5$ in ein Koordinatensystem.
Für die Zeichnung: Längeneinheit $1 cm$ ; $- 2 \leq x \leq 10; - 3 \leq y \leq 8$
Lösung zur Teilaufgabe a
Gehe beim Zeichnen der Drachenvierecke wie folgt vor:
Zeichne zunächst die beiden Geraden $g$ und $h$ ein.
Trage den Punkt $B_{1}$ (bzw. $B_{2}$ ) auf der Gerade $g$ an.
Da das Drachenviereck symmetrisch zur Gerade h ist, findest du $D_{1}$ (bzw. $D_{2}$ ), indem du $B_{1}$ (bzw. $B_{2}$ ), an $h$ spiegelst.
Der Schnittpunkt der Strecke $B_{1} D_{1}$ (bzw. $B_{2} D_{2}$ ) mit der Geraden $h$ ist $M_{1}$ (bzw. $M_{2}$ ).
Da $C_{1}$ (bzw. $C_{2}$ ) ebenfalls auf der Spiegelachse $h$ liegt und $\vec{A C_{1}} = 4 \cdot \vec{A M_{1}}$ (bzw. $\vec{A C_{2}} = 4 \cdot \vec{A M_{2}}$ ), kannst du nun auch $C_{1}$ (bzw. $C_{2}$ ) als Vierfaches der Streckenlänge $A M_{1}$ (bzw. $A M_{2}$ ) auf $h$ eintragen.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Bestimmen Sie rechnerisch die Koordinaten der Punkte $D_{n}$ in Abhängigkeit von der Abszisse $x$ der Punkte $B_{n}$ .

$[$ Ergebnis: $D_{n} (0,11 x - 0,92 | 1,04 x + 0,38)]$

Der Punkt $D_{3}$ liegt auf der y-Achse.
Berechnen Sie die Koordinaten des Punktes $B_{3}$ .

Lösung zur Teilaufgabe c
$D_{n} (0,11 x - 0,92 | 1,04 x + 0,38)$
Damit der Punkt auf der y-Achse liegt, muss die x-Koordinate 0 sein.
Berechne so die Abszisse x von $B_{3}$ :
$\begin{array}{rcll} 0,11 x - 0,92 & = & 0 & | + 0,92 \\ 0,11 x & = & 0,92 & | : 0,11 \\ x & = & 8,36 \end{array}$
Setze diese Abszisse in g ein:
$\begin{array}{l} y = - 0,3 \cdot 8,36 - 1 \\ y = - 3,51 \end{array}$
$\Rightarrow B_{3} (8,36 | - 3,51)$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechnen Sie die Koordinate der Punkte $M_{n}$ und $C_{n}$ in Abhängigkeit von der Abszisse $x$ der Punkte $B_{n}$ .
$[$ Ergebnis: $C_{n} (2,24 x - 1,84 | 1,48 x - 1,24)]$

Lösung zur Teilaufgabe d
1. Schritt: Koordinaten von $M_{n}$
Die Punkte $M_{n}$ liegen in der Mitte von $B_{n}$ und $D_{n}$ :
$B_{n} (x | - 0,3 x - 1), D_{n} (0,11 x - 0,92 | 1,04 x + 0,38)$
Berechne die Mitte dieser Punkte: $M_{n} (\frac{x + (0,11 x - 0,92)}{2} | \frac{(- 0,3 x - 1) + (1,04 x + 0,38)}{2}) =$
$M_{n} (0,56 x - 0,46 | 0,37 x - 0,31)$
2. Schritt: Koordinaten von $C_{n}$
Verwende die Eigenschaften aus der Angabe:
$\vec{A C_{n}} = 4 \cdot \vec{A M_{n}}$
$A (0 | 0), M_{n} (0,56 x - 0,46 | 0,37 x - 0,31)$
Da $A$ der Ursprung des Koordinatensystems ist, entsprechen $\vec{A C_{n}}$ und $\vec{A M_{n}}$ den Koordinaten von $C_{n}$ und $M_{n}$ .
Setze $M_{n}$ ein:
$(\begin{array}{c} x_{C_{n}} \\ y_{C_{n}} \end{array}) = 4 \cdot (\begin{array}{c} 0,56 x - 0,46 \\ 0,37 x - 0,31 \end{array})$
Verwende die skalare Multiplikation, um so weit wie möglich zusammenzufassen. $C_{n} (2,24 x - 1,84 | 1,48 x - 1,24)$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Das Drachenviereck $A B_{4} C_{4} D_{4}$ ist bei $B_{4}$ rechtwinklig.
Berechnen Sie den zugehörigen Wert für $x$ .

Lösung zur Teilaufgabe e
Damit zwei Vektoren senkrecht aufeinander stehen, muss ihr Skalarprodukt 0 sein.
Ein rechter Winkel bei $B_{4}$ bedeutet also, dass $\vec{A B_{4}} \circ \vec{B_{4} C_{4}} = 0$
1. Schritt: Stelle die Vektoren auf
$A (0 | 0), B_{n} (x | - 0,3 x - 1)$
$C_{n} (2,24 x - 1,84 | 1,48 x - 1,24)$
Bilde die Vektoren:
$\begin{aligned} \vec{A B_{n}} = & (\begin{array}{c} x \\ - 0,3 x - 1 \end{array}) \\ \vec{B_{n} C_{n}} = & (\begin{array}{c} 2,24 x - 1,84 - x \\ 1,48 x - 1,24 - (- 0,3 x - 1) \end{array}) \\ = & (\begin{array}{c} 1,24 x - 1,84 \\ 1,78 x - 0,24 \end{array}) \end{aligned}$
2. Schritt: Bilde das Skalarprodukt
$\vec{A B_{n}} \circ \vec{B_{n} C_{n}} = 0$
Setze die Vektoren ein und fasse so weit wie möglich zusammen.
$\begin{array}{rcl} x \cdot (1,24 x - 1,84) + (- 0,3 x - 1) \cdot (1,78 x - 0,24) & = & 0 \\ 1,24 x^{2} - 1,84 x - 0,53 x^{2} + 0,07 x - 1,78 x + 0,24 & = & 0 \\ 0,71 x^{2} - 3,55 x + 0,24 & = & 0 \end{array}$
Löse mithilfe der Lösungsformel für quadratischen Gleichung (Mitternachtsformel).
$x_{1 / 2} = \frac{3,55 \pm \sqrt{(- 3,55)^{2} - 4 \cdot 0,71 \cdot 0,24}}{2 \cdot 0,71}$
$x_{1} = 4,93$ , ( $x_{2} = 0,07$ )
$x_{2}$ liegt nicht in der Definitionsmenge.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Die Seite $[C_{5} D_{5}]$ des Drachenvierecks $A B_{5} C_{5} D_{5}$ verläuft parallel zur x-Achse.
Begründen Sie, dass gilt: $∢ D_{5} C_{5} B_{5} = {67,38}^{\circ}$

Lösung zur Teilaufgabe f
Der Steigungswinkel der Geraden $h$ und der Winkel $∢ D_{5} C_{5} A$ sind Wechselwinkel und somit gleich groß. Der Steigungswinkel ist aus Teilaufgabe b bekannt:
$∢ D_{5} C_{5} A = 33,69 °$
Der gesuchte Winkel $∢ D_{5} C_{5} B_{5}$ ist das Doppelte von $∢ D_{5} C_{5} A$ .
$∢ D_{5} C_{5} B_{5} = 2 \cdot 33,69 ° = 67,38 °$
Wenn du möchtest, kannst du dir im folgenden Video eine Schritt-für-Schritt Lösung der Aufgabe anschauen.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das?

$m_{h}$	$=$	$\frac{2}{3}$
	↓	Nutze hierzu den Zusammenhang $m_{g} = t a n (α)$ .
$\tan (α)$	$=$	$\frac{2}{3}$	$\tan^{- 1}$
	↓	Forme nach $α$ um:
$α$	$=$	$33,69 °$

$D_{n}$	$=$	$(\begin{array}{c} x^{'} \\ y^{'} \end{array})$
	$=$	$(\begin{array}{cc} \cos 2 α & \sin 2 α \\ \sin 2 α & - \cos 2 α \end{array}) \cdot (\begin{array}{c} x \\ y \end{array})$
	↓	Setze den Punkt $B_{n}$ und den Winkel $α$ in die Abbildungsgleichung ein:
	$=$	$(\begin{array}{cc} \cos (2 \cdot 33,69 °) & \sin (2 \cdot 33,69 °) \\ \sin (2 \cdot 33,69 °) & - \cos (2 \cdot 33,69 °) \end{array}) \cdot (\begin{array}{c} x \\ - 0,3 x - 1 \end{array})$
	↓	Berechne die Werte von Sinus und Kosinus.
	$=$	$(\begin{array}{cc} 0,38 & 0,92 \\ 0,92 & - 0,38 \end{array}) \cdot (\begin{array}{c} x \\ - 0,3 x - 1 \end{array})$
	↓	Führe die Matrix-Vektor-Multiplikation durch. Beachte, dass du weiterhin auf zwei Nachkommastellen runden darfst.
	$=$	$(\begin{array}{c} 0,38 x - 0,27 x - 0,92 \\ 0,92 x + 0,12 x + 0,38 \end{array})$
	↓	Fasse zusammen.
	$=$	$(\begin{array}{c} 0,11 x - 0,92 \\ 1,04 x + 0,38 \end{array})$

Lösung zur Teilaufgabe a

Gehe beim Zeichnen der Drachenvierecke wie folgt vor:

Hast du eine Frage oder Feedback?

Lösung zur Teilaufgabe b

1. Schritt: Berechne den Winkel $α$ , den die Gerade h mit der x-Achse einschließt

2. Schritt: Abbildungsgleichung aufstellen

Hast du eine Frage oder Feedback?

Lösung zur Teilaufgabe c

Hast du eine Frage oder Feedback?

Lösung zur Teilaufgabe d

1. Schritt: Koordinaten von $M_{n}$

2. Schritt: Koordinaten von $C_{n}$

Hast du eine Frage oder Feedback?

Lösung zur Teilaufgabe e

1. Schritt: Stelle die Vektoren auf

2. Schritt: Bilde das Skalarprodukt

Hast du eine Frage oder Feedback?

Lösung zur Teilaufgabe f

Hast du eine Frage oder Feedback?

Lösung zur Teilaufgabe a

Gehe beim Zeichnen der Drachenvierecke wie folgt vor:

Hast du eine Frage oder Feedback?

Lösung zur Teilaufgabe b

1. Schritt: Berechne den Winkel α, den die Gerade h mit der x-Achse einschließt

2. Schritt: Abbildungsgleichung aufstellen

Hast du eine Frage oder Feedback?

Lösung zur Teilaufgabe c

Hast du eine Frage oder Feedback?

Lösung zur Teilaufgabe d

1. Schritt: Koordinaten von Mn

2. Schritt: Koordinaten von Cn

Hast du eine Frage oder Feedback?

Lösung zur Teilaufgabe e

1. Schritt: Stelle die Vektoren auf

2. Schritt: Bilde das Skalarprodukt

Hast du eine Frage oder Feedback?

Lösung zur Teilaufgabe f

Hast du eine Frage oder Feedback?

1. Schritt: Berechne den Winkel $α$ , den die Gerade h mit der x-Achse einschließt

1. Schritt: Koordinaten von $M_{n}$

2. Schritt: Koordinaten von $C_{n}$