Aufgabe 2A
Ein Telefonanbieter bietet die Tarife S, M, und L an. Jeder Kunde hat genau einen dieser Tarife. Allen Kunden steht eine Service-Hotline zur Verfügung.
aller Kunden haben den Tarif S, den Tarif L. aller Kunden haben bereits die Service-Hotline angerufen. der Kunden haben den Tarif M und haben bereits die Service-Hotline angerufen.
haben den Tarif S und haben die Service-Hotline noch nicht angerufen.
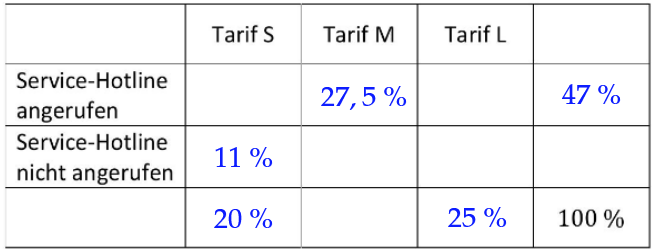
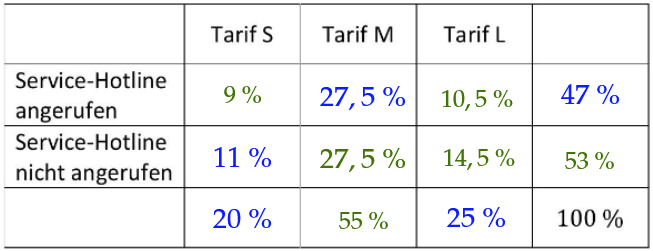
Stellen Sie alle Anteile - analog zu einer Vier-Felder-Tafel - in der folgenden Tabelle dar.
(3 BE)
Ein zufällig ausgewählter Kunde hat die Service-Hotline noch nicht angerufen.
Bestimmen Sie die Wahrscheinlichkeit dafür, dass dieser Kunde den Tarif S hat.
(2 BE)
Bestimmen Sie den Anteil aller Kunden, die entweder den Tarif haben oder die Service-Hotline noch nicht angerufen haben. (2 BE)
Der Anbieter führt eine Befragung unter 600 zufällig ausgewählten Kunden durch. Es kann davon ausgegangen werden, dass unter den Befragten die Anzahl derjenigen mit dem Tarif binomialverteilt ist.
Beschreiben Sie die Bedeutung des folgenden Terms im Sachzusammenhang: (3 BE)
Berechnen Sie die Wahrscheinlichkeit dafür, dass die Anzahl der Kunden mit dem Tarif S um höchstens vom Erwartungswert abweicht. (3 BE)
Bestimmen Sie die größte natürliche Zahl , für die die Wahrscheinlichkeit dafür, dass unter den Befragten weniger als Kunden den Tarif haben, kleiner als ist. (4 BE)
Die Wartezeit beim Anrufen der Service-Hotline ist normalverteilt mit einer Standardabweichung von 1 Minute und 15 Sekunden.
Angenommen, die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Anrufer höchstens drei Minuten warten muss, beträgt .
Berechnen Sie unter dieser Annahme die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Anrufer mindestens fünf Minuten warten muss. (4 BE)
Untersuchen Sie, ob es ein Zeitintervall mit einer Länge von zwei Minuten gibt, in dem die Wartezeit eines zufällig ausgewählten Anrufers mit einer Wahrscheinlichkeit von mindestens liegt. (4 BE)
Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen