Aufgaben zum Sinus, Kosinus und Tangens im rechtwinkligen Dreieck
Hier findest du gemischte Aufgaben zu den Winkelfunktionen im Dreieck. Lerne, Sinus, Kosinus und Tangens im rechtwinkligen Dreieck anzuwenden!
- 1
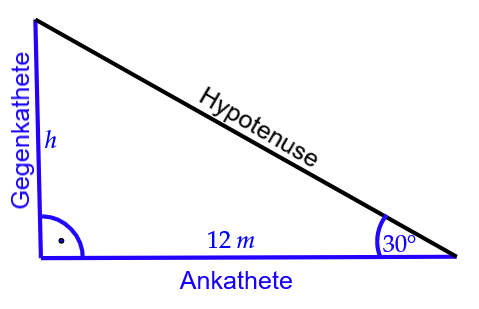
Höhe eines Baums
Der Baum wirft bei schönem Wetter einen Schatten, mit der Länge .
Gemessen wird der Schatten unter einem Winkel von .
Berechne die Höhe des Baums.
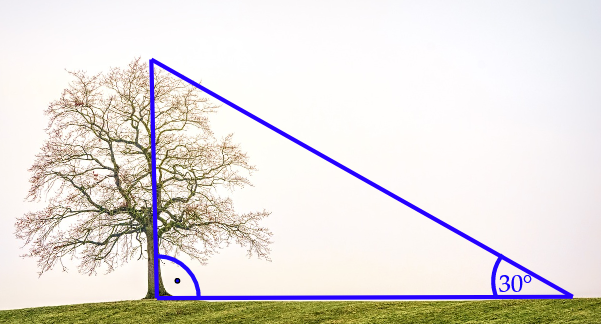
Skizze des Baums
- 2
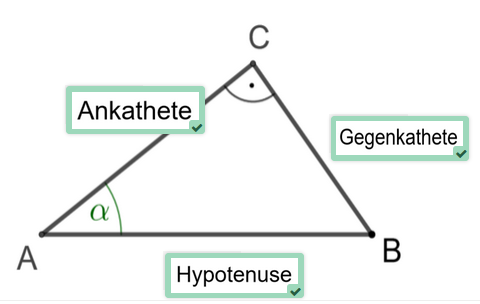
Seiten im rechtwinkligen Dreieck
Ordne die Begriffe den richtigen Seiten im Dreieck zu.
Welche der aufgestellten Gleichungen ist richtig?
- 3
Berechne die Seiten
Berechne die fehlenden Seiten der Dreiecke. Runde auf zwei Dezimalstellen.
Berechne .
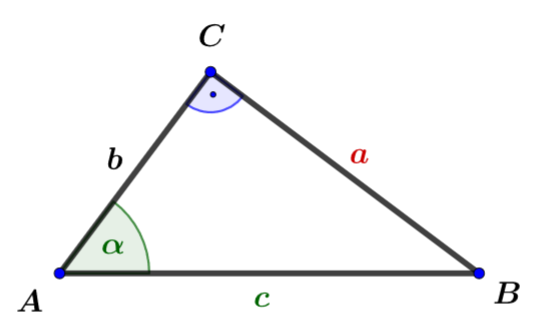
Skizze
Berechne .
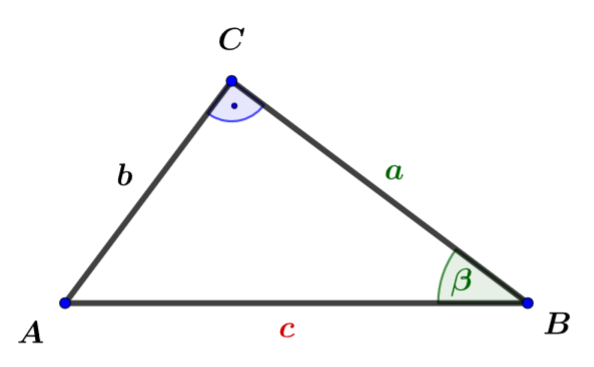
Berechne .
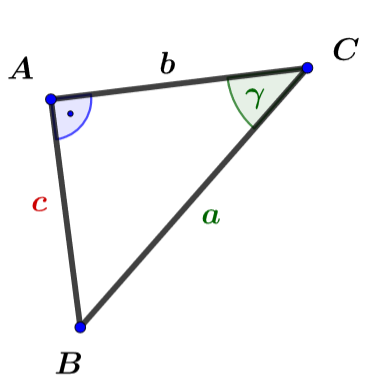
- 4
Schattenwurf
Heike ist groß. Wie lang ist ihr Schatten, wenn die Sonnenstrahlen in einem Winkel von auf den Boden auftreffen?
Gib das Ergebnis in Metern auf 2 Dezimalstellen gerundet an.

Schatten von Heike
m - 5
Winkel gesucht
Diese nicht maßstabsgetreue Skizze zeigt ein Rechteck mit den Seitenlängen und .
Berechne den Winkel in ganzen Grad.
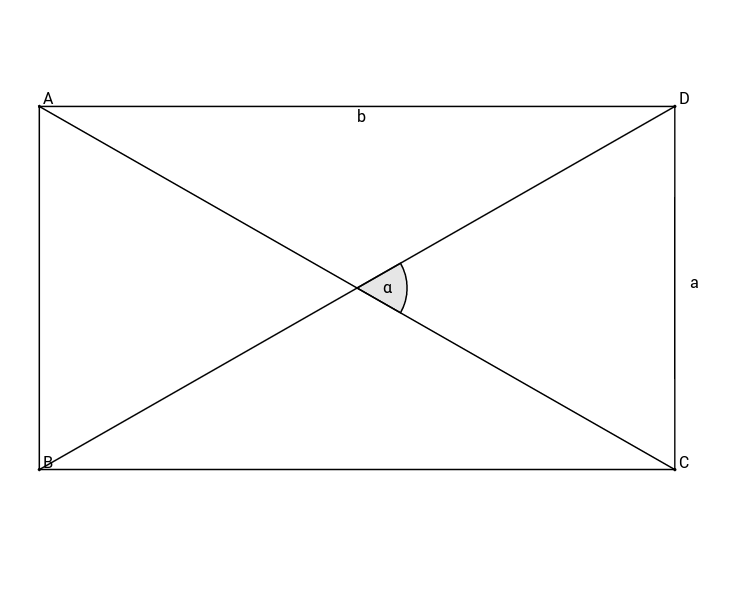
Skizze der Aufgabe
° - 6
Rechnen im Dreieck
Diese Skizze zeigt ein nicht maßgetreues, rechtwinkliges Dreieck mit der Höhe und den Winkeln und .
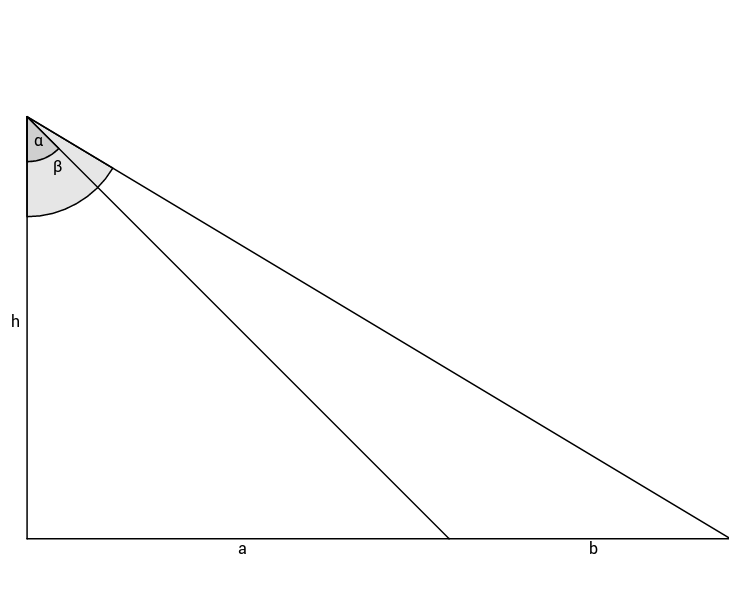
Skizze der Aufgabe
Berechne die Seitenlänge . Runde dabei auf zwei Dezimalstellen.
cmBerechne die Seitenlänge . Runde dabei auf zwei Dezimalstellen.
cm
- 7
Der Umfang der Erde
Der griechische Mathematiker Eratosthenes hat vor über 2000 Jahren den Umfang der Erde berechnet.
Dazu brauchte er nur zwei Orte:
Einen tiefen Brunnen in Assuan und
den Obelisken in Alexandria
Sobald die Sonne genau über dem Brunnen in Assuan stand, wurde in Alexandria vermessen, wie groß der Schatten am Obelisk war.
Wie Eratosthenes werden wir auf diese Weise den Umfang der Erde berechnen.
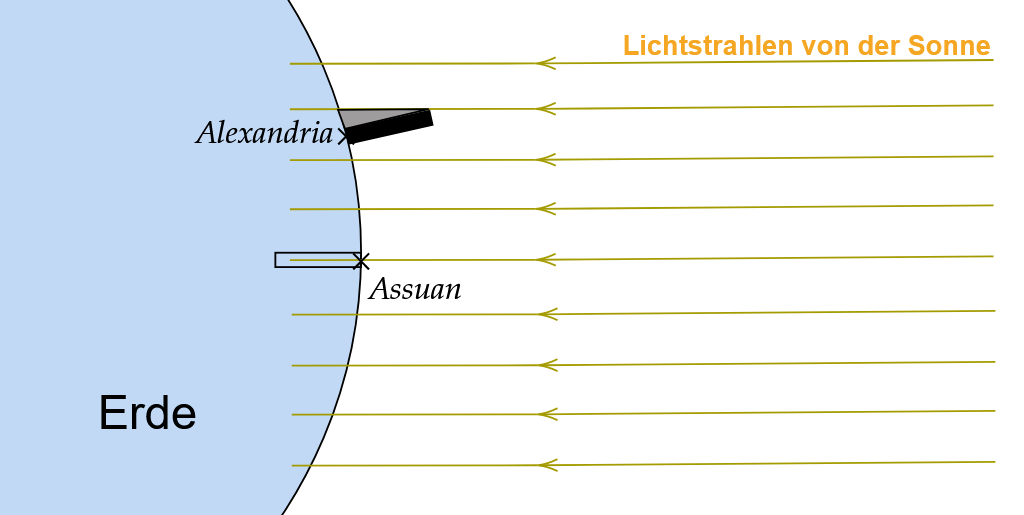
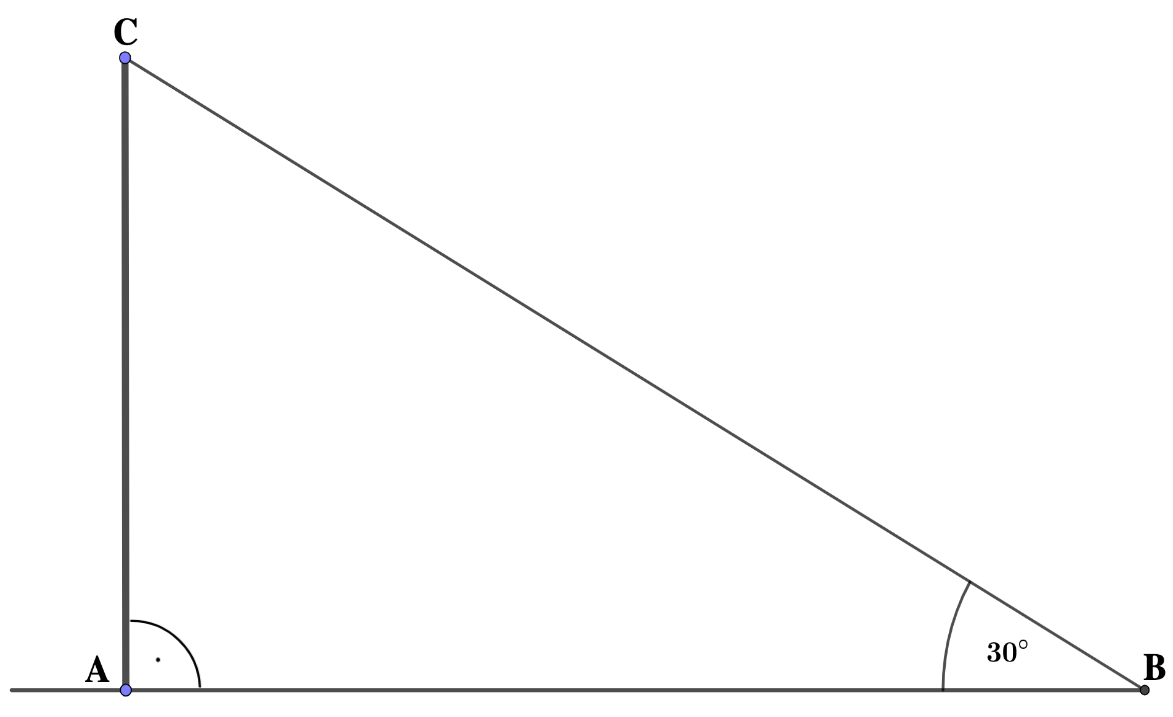
Skizze des Aufbaus
Schatten in Alexandria
In Alexandria befindet sich der Obelisk der Kleopatra.
Er ist hoch und warf einen Schatten von .
Berechne den Winkel in der Spitze des Obelisken. Runde dabei auf zwei Stellen.

Skizze des Dreiecks am Obelisk
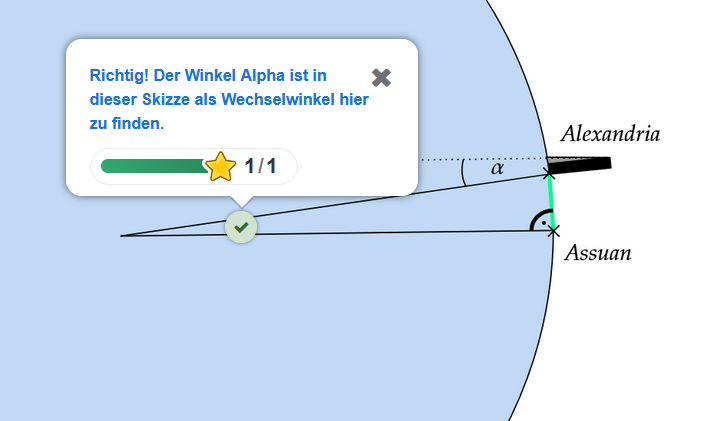
°Die Suche nach dem Winkel
Der Winkel am Obelisk ist sehr wichtig. In der Skizze ist noch einmal zu finden, klicke ihn an!
Der Umfang der Erde
Die Strecke von Alexandria nach Assuan wurde von den Soldaten des Pharaos abmarschiert, um sie zu messen:
Diese Strecke steht zum Erdumfang im gleichen Verhältnis, wie der Winkel zum vollen Winkel .
Berechne damit den Erdumfang in ganzen .
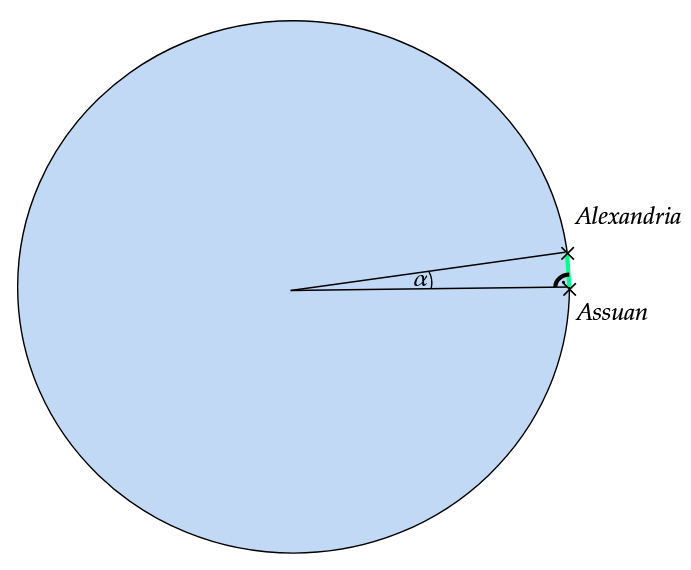
Skizze der Erde
km
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?