Aufgabe 2A
Ein Institut für Ernährungsforschung untersucht die Essgewohnheiten von in Deutschland lebenden Personen einer bestimmten Altersgruppe. Im Folgenden wird davon ausgegangen, dass sich der Personen der betrachteten Gruppe häufig von Fertiggerichten ernähren.
Es werden Personen der betrachteten Gruppe zufällig ausgewählt.
Bestimmen Sie die Wahrscheinlichkeit dafür, dass sich mindestens ein Viertel dieser
Personen häufig von Fertiggerichten ernährt. [3 BE]
Beschreiben Sie im Sachzusammenhang ein Zufallsexperiment, bei dem die
Wahrscheinlichkeit eines Ereignisses mit dem Term
berechnet werden kann. Geben Sie dieses Ereignis an. [4 BE]
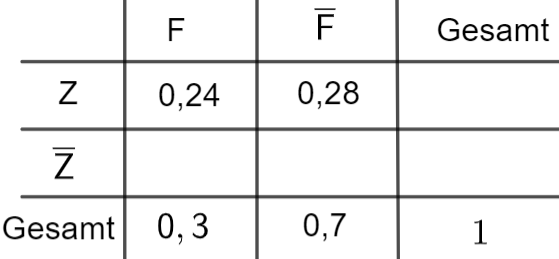
Neben der Ernährung durch Fertiggerichte wird auch der Verzehr von Zucker untersucht. Der Anteil der Personen der betrachteten Gruppe, die sich häufig von Fertiggerichten ernähren und zu viel Zucker verzehren, beträgt .
Der Anteil der Personen, die zu viel Zucker verzehren, ist unter denjenigen, die sich häufig von Fertiggerichten ernähren, doppelt so groß wie unter denjenigen, die sich nicht häufig von Fertiggerichten ernähren. Aus der betrachteten Gruppe wird eine Person zufällig ausgewählt.
Untersucht werden folgende Ereignisse:
: „Die Person ernährt sich häufig von Fertiggerichten.“
: „Die Person verzehrt zu viel Zucker.“
Weisen Sie nach, dass die Wahrscheinlichkeit dafür, dass die ausgewählte Person zu viel
Zucker verzehrt und sich nicht häufig von Fertiggerichten ernährt, beträgt. [4 BE]
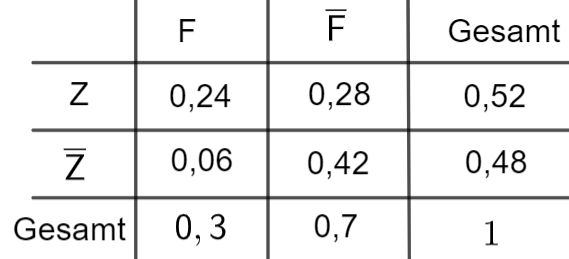
Stellen Sie den Sachverhalt in einer vollständig ausgefüllten Vierfeldertafel dar. [3 BE]
Das Institut untersucht den Anteil der Personen der betrachteten Gruppe, die einen
bestimmten zuckerfreien Müsliriegel gegenüber einem vergleichbaren zuckerhaltigen
Müsliriegel bevorzugen.
Aufgrund früherer Untersuchungen wird von einem Anteil von ausgegangen.
Bei einer Umfrage unter Personen der
betrachteten Gruppe gaben Personen an, den zuckerfreien Müsliriegel zu bevorzugen.
Abgebildet sind die Graphen der für
definierten Funktionen
und
.
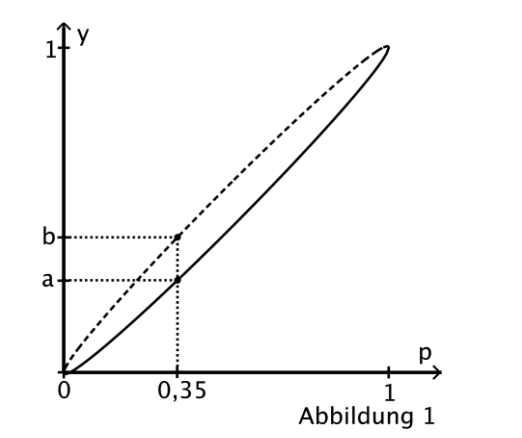
Geben Sie die Werte von und an.
Interpretieren Sie das Ergebnis der Umfrage im Hinblick auf die Bedeutung des Intervalls (vgl. Abbildung 1). [4 BE]
Nach der Durchführung einer Werbemaßnahme für den zuckerfreien Müsliriegel möchte das Institut Anhaltspunkte darüber gewinnen, wie groß der Anteil inzwischen ist.
In der betrachteten Gruppe wurden daraufhin Personen befragt.
Die Auswertung ergab, dass etwa der befragten Personen den zuckerfreien Riegel bevorzugen. Das zugehörige -Konfidenzintervall, dessen Ränder mit den Gleichungen
und
ermittelt werden, besitzt eine Länge, die kleiner als ist.
Zeigen Sie, dass der kleinstmögliche Wert von zwischen und liegt. [7 BE]
Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen