Aufgabe 3A
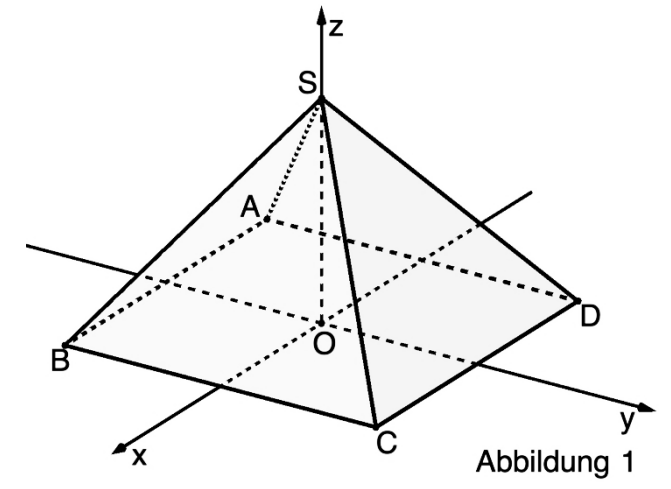
Abbildung 1 zeigt die Pyramide mit den Eckpunkten , ,
, und sowie den Punkt , der in der quadratischen Grundfläche der Pyramide liegt.
Die Seitenfläche der Pyramide liegt in der Ebene .
Berechnen Sie den Inhalt der Oberfläche der Pyramide. [4 BE]
Bestimmen Sie eine Gleichung von in Koordinatenform. [3 BE]
[Zur Kontrolle: ]
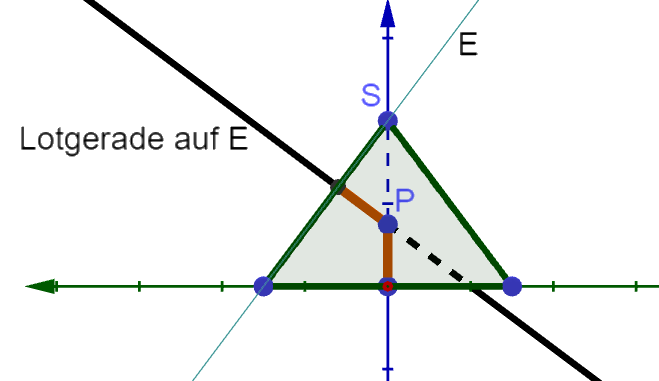
Es gibt einen Punkt , der im Innern der Pyramide liegt und von allen vier
Seitenflächen sowie der Grundfläche der Pyramide den gleichen Abstand hat. Mithilfe
des folgenden Gleichungssystems lässt sich der Wert von bestimmen:
Geben Sie die geometrische Bedeutung dieser Gleichungen an. [5 BE]
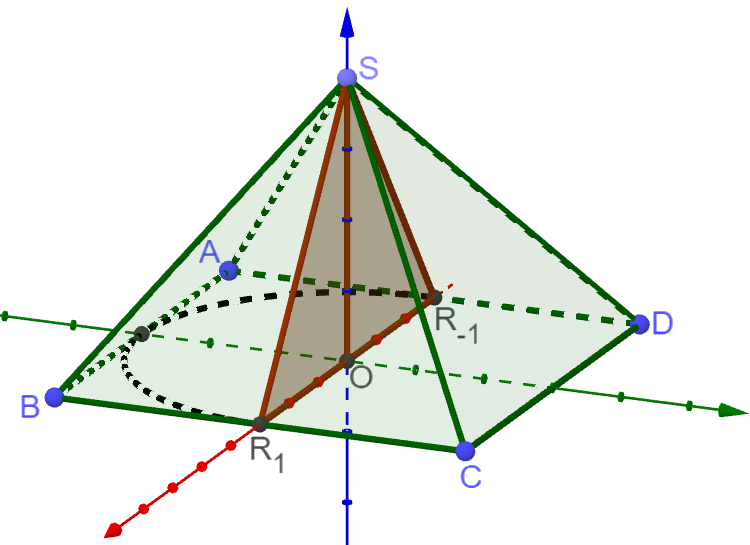
Die Ebene gehört zur Schar der Ebenen mit
. Die Seitenfläche der Pyramide liegt in der Ebene der Schar, die Seitenfläche in der Ebene .
Zeigen Sie, dass der Punkt in allen Ebenen der Schar enthalten ist. [2 BE]
Weisen Sie nach, dass die Größe des Winkels, unter dem die Gerade die Ebene
schneidet, unabhängig von ist. Bestimmen Sie die Größe dieses Winkels. [5 BE]
Jede Ebene der Schar schneidet die
xy-Ebene in einer Gerade . Mit wird jeweils derjenige Punkt auf bezeichnet, der von den kleinsten Abstand hat. In Abbildung 2 sind und beispielhaft für eine Ebene der Schar dargestellt.
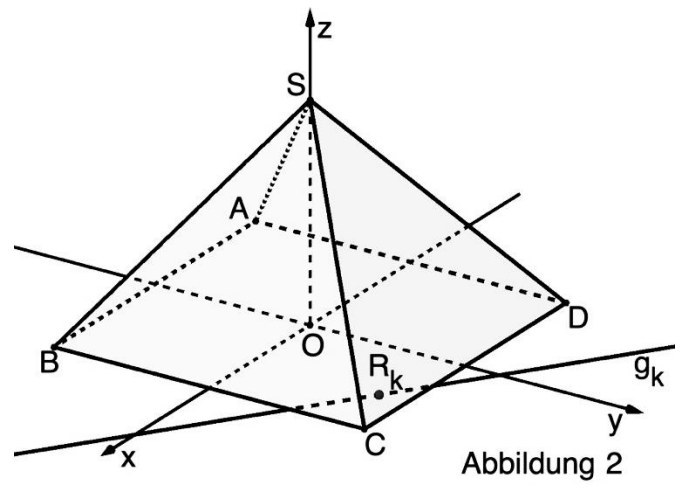
Zeichnen Sie die Punkte und in Abbildung 2 ein. [3 BE]
Durchläuft alle Werte von bis , dann dreht sich die Fläche um die Strecke . Dabei entsteht ein Körper. Beschreiben Sie die Form des entstehenden Körpers und bestimmen Sie das Volumen dieses Körpers. [3 BE]
Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen