Wahlteil - GTR - lernen mit Serlo!

Aufgabe 1A

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f$ mit

$f(x)=\frac{3}{1000}\cdot x^4 −\frac{8}{100}\cdot x^3 + \frac{6}{10}\cdot x^2$ .

Die Abbildung 1 zeigt den Graphen von $f$ sowie den Punkt $P(0|−\frac58)$ .

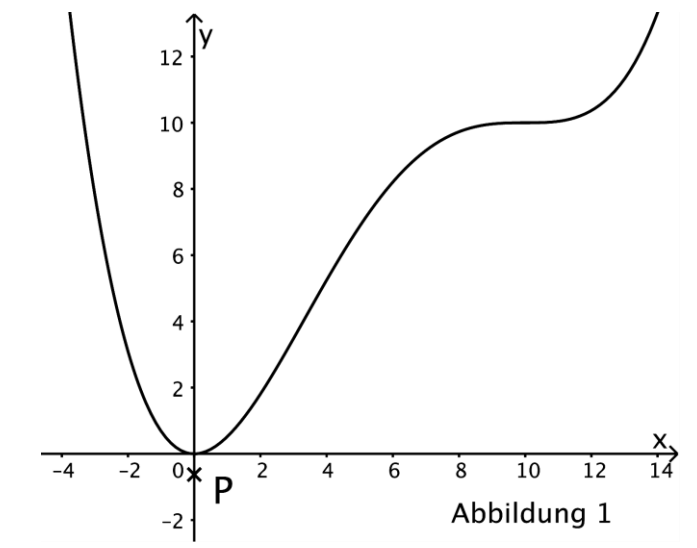
Der Graph von $f$ besitzt den Tiefpunkt $(0 ∣ 0)$ .
Zeigen Sie, dass der Graph von $f$ keine weiteren Extrempunkte besitzt. [4 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion
Zeige, dass der Graph von $f$ keine weiteren Extrempunkte besitzt
$f^{'} (x)$ besitzt für $x = 0$ und für $x = 10$ eine Nullstelle.
Bei $x = 0$ besitzt der Graph von $f$ den Tiefpunkt $(0 ∣ 0)$ .
Zusammen mit der Abbildung ergibt sich, dass der Graph von $f$ für $x = 10$ einen Sattelpunkt (Terrassenpunkt) hat.
Da $f$ eine ganzrationale Funktion vierten Grades ist, besitzt der Graph von $f$ keine weiteren Extrempunkte.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
$f^{'} (x)$ besitzt für $x = 0$ und für $x = 10$ eine Nullstelle.
Betrachte den Graphen.
Die Gerade durch die Punkte $P (0 ∣ - 0,625)$ und $Q (- 0,25 ∣ - 1)$ wird mit $t$ bezeichnet.
Ermitteln Sie eine Gleichung von $t$ .
Weisen Sie rechnerisch nach, dass $t$ die Tangente an den Graphen von $f$ im Punkt
$(5 ∣ f (5))$ ist. [5 BE]
[Zur Kontrolle: Gleichung von $𝑡 : 𝑦 = 1,5 𝑥 - 0,625$ ]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Ermittle eine Gleichung von $t$
Aus $P$ entnimmt man den y-Achsenabschnitt $b = - 0,625$ .
Setze in $y=m \cdot x+b= m \cdot x-0{,}625$ die Koordinaten von $Q$ ein:
$-1=m \cdot \left(-0{,}25\right)-0{,}625\;\Rightarrow\;-0{,}375=m \cdot \left(-0{,}25\right)\;\Rightarrow\;m=1{,}5$
Damit erhält man:
$\displaystyle t:y=1{,}5\cdot x-0{,}625$
Weise rechnerisch nach, dass $t$ die Tangente an den Graphen von $f$ im Punkt $(5 ∣ f (5))$ ist
$t$ ist Tangente an den Graphen von $f$ im Punkt $(5 ∣ f (5))$ , wenn:
$f (5) = t (5)$
$f^{'} (5) = m_{t}$
Berechne: $f (5) = 6,875$ und $t(5)=6{,}875 \;\Rightarrow\;f(5)=t(5)\;\checkmark$
$f^{'} (5) = 1,5$ und $m_t=1{,}5\;\Rightarrow\;f'(5)=m_t\;\checkmark$
Beide Bedingungen sind erfüllt:
$\Rightarrow\;t$ ist die Tangente an den Graphen von $f$ im Punkt $(5 ∣ f (5))$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Teil 1
Aus $P$ entnimmt man den y-Achsenabschnitt $b$ .
Setze in $y=m \cdot x+b$ die Koordinaten von $Q$ ein.
Teil 2
$t$ ist Tangente an den Graphen von $f$ im Punkt $(5 ∣ f (5))$ , wenn $f (5) = t (5)$ und $f^{'} (5) = m_{t}$ .
Der Graph von $f$ und die Tangente $t$ schließen eine Fläche ein, die aus zwei Flächenstücken besteht.
Bestimmen Sie den Inhalt dieser Fläche. [6 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
Berechne den Inhalt dieser Fläche
Für die Integrationsgrenzen berechne $f (x) = t (x)$ :
$f (x) = t (x)$ hat die relevanten Schnittstellen $x_1\approx0{,}52$ und $x_2\approx16{,}15$ .
Berechne den Flächeninhalt:
$A=\displaystyle\int_{x_1}^{x_2}(1{,}5x-0{,}625-f(x))\;\mathrm{d}x\approx44{,}59$
Der gesuchte Flächeninhalt beträgt rund $44{,}6 \;\text{FE}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Für die Integrationsgrenzen berechne $f (x) = t (x)$ $\;\Rightarrow\;$ relevante Schnittstellen $x_{1}$ und $x_{2}$ .
Berechne den Flächeninhalt: $A=\displaystyle\int_{x_1}^{x_2}(t(x)-f(x))\;\mathrm{d}x$
Der Graph der in $\mathbb{R}$ definierten Funktion $g$ kann aus dem Graphen von $f$ erzeugt
werden. Der Punkt $(12 ∣ 12)$ des Graphen von $g$ wird dabei aus dem Punkt $(10 ∣ 10)$ des
Graphen von $f$ erzeugt und für alle $x\in\mathbb{R}$ gilt $𝑔(𝑥) = 𝑎 \cdot 𝑓(𝑏 ⋅ 𝑥)$ mit $a,b \in\mathbb{R}^+$
Geben Sie in diesem Zusammenhang die Bedeutung von $a$ und $b$ an und
berechnen Sie die Werte von $𝑎$ und $𝑏$ . [4 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Transformationen von Funktionen
Gib in diesem Zusammenhang die Bedeutung von $a$ und $b$ an
Die Funktion $f$ wird mit dem Faktor $a$ in y-Richtung gestreckt und anschließend mit dem Faktor $\dfrac{1}{b}$ in x-Richtung gestreckt.
$\underbrace{f\xrightarrow{\cdot a}a\cdot f}_\text{Streckung in y-Richt.mit Faktor a}\;\underbrace{\xrightarrow{f(b\cdot x)}a\cdot f(b\cdot x)}_{\text{Streckung in x-Richt.mit Faktor\;}\frac{1}{b}}=g(x)$
Berechne die Werte von $𝑎$ und $𝑏$
Der Punkt $(12 ∣ 12)$ des Graphen von $g$ wird dabei aus dem Punkt $(10 ∣ 10)$ des
Graphen von $f$ erzeugt:
$\Rightarrow\; g(12)=a\cdot f(10)\;\Rightarrow\;12=a\cdot 10\;\Rightarrow\;a=\dfrac{6}{5}$
Weiterhin folgt: $12=\dfrac{1}{b}\cdot 10\;\Rightarrow\;b=\dfrac{5}{6}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Teil 1
Es handelt sich einmal um eine Streckung in y-Richtung und um eine Streckung in x-Richtung.
Teil 2
Der Punkt $(12 ∣ 12)$ des Graphen von $g$ wird dabei aus dem Punkt $(10 ∣ 10)$ des Graphen von $f$ erzeugt. Stelle zwei Gleichungen zur Berechnung von $a$ und $b$ auf.
Zwei Radfahrer starten gleichzeitig nebeneinander. Die Geschwindigkeit von Radfahrer $F$ wird in den ersten $10$ Sekunden (s) nach dem Start durch die Funktion $f$ mit $f(x) =\frac3{1000}\cdot x^4 −\frac8{100}\cdot x^3 +\frac6{10}\cdot x^2$
beschrieben. Die Geschwindigkeit von Radfahrer $H$ wird in den ersten $12$ Sekunden nach dem Start
durch die in $\mathbb{R}$ definierte Funktion $h$ mit $h(x) =\frac1{576}\cdot x^4 −\frac1{18}\cdot x^3 +\frac{1}{2}\cdot x^2$ beschrieben.
Dabei ist $x$ die seit dem Start vergangene Zeit in Sekunden und $f (x)$ bzw. $h (x)$ die
Geschwindigkeit in Meter pro Sekunde $(\frac{\text{m}}{\text{s}})$ .
Bestimmen Sie die Geschwindigkeit von Radfahrer $F$ drei Sekunden nach dem Start
sowie den Zeitpunkt, zu dem er eine Geschwindigkeit von $8\;\frac{\text{m}}{\text{s}}$ erreicht. [4 BE]
Abbildung 2
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionswert
Berechne $f (3)$ :
$f (3) = 3,483$
Die Geschwindigkeit beträgt etwa $3{,}5 \;\frac{\text{m}}{\text{s}}$ .
$f (x) = 8$ hat im betrachteten Zeitraum die Lösung $x \approx5{,}82$ , d. h. die
Geschwindigkeit wird etwa $5,8$ Sekunden nach dem Start erreicht.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Teil 1
Berechne $f (3)$ .
Teil 2
Bestimme die Lösung von $f (x) = 8$ .
Nach den ersten $12$ Sekunden fährt Radfahrer $H$ mit konstanter Geschwindigkeit.
Geben Sie diese konstante Geschwindigkeit an.
Zeigen Sie durch Rechnung, dass der zum Radfahrer $H$ gehörende Graph in der
Abbildung 2 an der Stelle $12$ eine waagerechte Tangente aufweist. [4 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente an Graph
Gib diese konstante Geschwindigkeit an
Bestimme $h (12)$ :
$h (12) = 12$
Die konstante Geschwindigkeit beträgt $12\;\frac{\text{m}}{\text{s}}$ .
Zeige durch Rechnung, dass der zum Radfahrer $H$ gehörende Graph in der Abbildung 2 an der Stelle $12$ eine waagerechte Tangente aufweist
Bestimme $h^{'} (12)$ :
$h^{'} (12) = 0$ , d.h. die Tangente hat an der Stelle $x = 0$ die Steigung null (waagrechte Tangente).
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Teil 1
Bestimme $h (12)$ .
Teil 2
Bestimme $h^{'} (12)$ .
Nach dem Start gibt es genau einen Zeitpunkt, zu dem die Geschwindigkeiten beider
Radfahrer gleich groß sind. Im Modell wird dieser Zeitpunkt mit $x_{s}$ bezeichnet.
Berechnen Sie $x_{s}$ . [3 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte zweier Funktionen berechnen
Berechne $x_{s}$
$f (x) = h (x)$ hat für $0 < x < 10$ die Lösung $x_s \approx5{,}88$ .
Der Zeitpunkt, zu dem die Geschwindigkeiten beider Radfahrer gleich groß sind, ist etwa $5,88$ Sekunden nach dem Start.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Suche die Lösung von $f (x) = h (x)$ für $0 < x < 10$ .
Es gibt genau einen Zeitpunkt in den ersten $10$ Sekunden nach dem Start, zu dem einer
der beiden Radfahrer den anderen überholt.
Berechnen Sie, um wieviel Prozent die Geschwindigkeit des schnelleren Radfahrers die
Geschwindigkeit des langsameren Radfahrers zum Zeitpunkt des Überholens übersteigt.
[5 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
Berechne, um wieviel Prozent die Geschwindigkeit des schnelleren Radfahrers die Geschwindigkeit des langsameren Radfahrers zum Zeitpunkt des Überholens übersteigt
Der zurückgelegte Weg muss beim Überholen für beide Radfahrer gleich groß sein, d.h. das $\displaystyle\int_{0}^{z}(f(x)-h(x))\;\mathrm{d}x$ muss gleich null sein (gleicher zurückgelegter Weg).
$\displaystyle\int_{0}^{z}(f(x)-h(x))\;\mathrm{d}x=0$
Für $0 < z < 10$ erhält man die Lösung $z_1\approx8{,}31$ .
Berechne die prozentuale Änderung:
Es ist $\dfrac{h(z_1)-f(z_1)}{f(z_1)}\approx 0{,}11=11\;\%$
Um $11 %$ Prozent übersteigt die Geschwindigkeit des schnelleren Radfahrers die Geschwindigkeit des langsameren Radfahrers zum Zeitpunkt des Überholens.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Der zurückgelegte Weg muss beim Überholen für beide Radfahrer gleich groß sein, d.h. das $\displaystyle\int_{0}^{z}(f(x)-h(x))\;\mathrm{d}x$ muss gleich null sein (gleicher zurückgelegter Weg).
Man erhält für $0 < z < 10$ die Lösung $z_{1}$ .
Berechne mit dem Wert $z_{1}$ die prozentuale Änderung.

Aufgabe 1A

Zeige, dass der Graph von fff keine weiteren Extrempunkte besitzt

Hast du eine Frage oder Feedback?

Ermittle eine Gleichung von ttt

Weise rechnerisch nach, dass ttt die Tangente an den Graphen von fff im Punkt (5∣f(5))(5|f(5))(5∣f(5)) ist

Hast du eine Frage oder Feedback?

Berechne den Inhalt dieser Fläche

Hast du eine Frage oder Feedback?

Gib in diesem Zusammenhang die Bedeutung von aaa und bbb an

Berechne die Werte von 𝑎𝑎a und 𝑏𝑏b

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Gib diese konstante Geschwindigkeit an

Zeige durch Rechnung, dass der zum Radfahrer HHH gehörende Graph in der Abbildung 2 an der Stelle 121212 eine waagerechte Tangente aufweist

Hast du eine Frage oder Feedback?

Berechne xsx_sxs​

Hast du eine Frage oder Feedback?

Berechne, um wieviel Prozent die Geschwindigkeit des schnelleren Radfahrers die Geschwindigkeit des langsameren Radfahrers zum Zeitpunkt des Überholens übersteigt

Hast du eine Frage oder Feedback?

Zeige, dass der Graph von $f$ keine weiteren Extrempunkte besitzt

Ermittle eine Gleichung von $t$

Weise rechnerisch nach, dass $t$ die Tangente an den Graphen von $f$ im Punkt $(5 ∣ f (5))$ ist

Gib in diesem Zusammenhang die Bedeutung von $a$ und $b$ an

Berechne die Werte von $𝑎$ und $𝑏$

Zeige durch Rechnung, dass der zum Radfahrer $H$ gehörende Graph in der Abbildung 2 an der Stelle $12$ eine waagerechte Tangente aufweist

Berechne $x_{s}$