Nachtermin Teil A
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
- 1
Aufgabe A 1
In einem Säckchen befinden sich sechs Kugeln gleicher Art. Drei Kugeln sind als Niete („N“), eine Kugel ist als Joker („J“) und zwei Kugeln sind als Gewinn („G“) gekennzeichnet. Man zieht zufällig eine Kugel. Beim Joker darf man ein zweites Mal ziehen. Ansonsten darf man keine weitere Kugel ziehen. Es werden keine Kugeln zurück ins Säckchen gelegt.
Zeichnen Sie ein zugehöriges Baumdiagramm, in dem alle Anteile ersichtlich sind. (2 P)
Berechnen Sie die Wahrscheinlichkeit dafür, dass man am Ende eine als Gewinn
gekennzeichnete Kugel gezogen hat. (2 P)
- 2
Aufgabe A 2
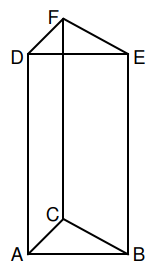
Das gleichschenklig-rechtwinklige Dreieck ist die Grundfläche des geraden Prismas mit einem Volumen von (vgl. Skizze).
Es gilt: .
Berechnen Sie die Länge der Strecke .
(2 P)
- 3
Aufgabe A 3
Die Parabel hat die Gleichung .
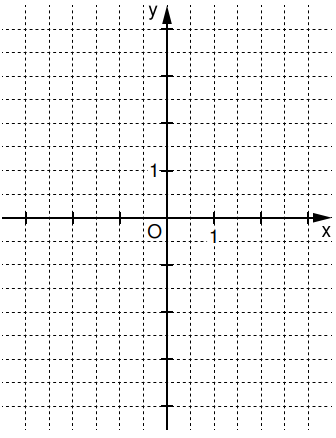
Zeichnen Sie die Parabel für in das Koordinatensystem ein. (1,5 P)
- 4
Aufgabe A 4
Die Parabel hat die Gleichung
Berechnen Sie die Koordinaten des Scheitelpunktes der Parabel . (2 P)
- 5
Aufgabe A 5
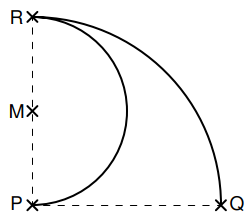
Nebenstehende Skizze zeigt den Halbkreisbogen mit dem Mittelpunkt und dem Radius sowie den Viertelkreisbogen mit dem Mittelpunkt und dem Radius .
Zeigen Sie, dass die beiden Kreisbögen und gleich lang sind. (2 P)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?


