Teil B, Gruppe 2

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

1
Löse folgende Gleichungen
1. $(2{,}5x−10)\cdot0{,}6−0{,}4x+3{,}5=3{,}75−0{,}5\cdot(0{,}6x−1{,}5)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Grundrechenarten
  Ausmultiplizieren der Klammern
  $1{,}5x−6−0{,}4x+3{,}5=3{,}75−0{,}3x+0{,}75$
  X auf eine Seite bringen
  $1{,}5x-0{,}4x+0{,}3x = 6-3{,}5+3{,}75+0{,}75$
  Vereinfachen
  $1{,}4x=7$
  Endergebnis
  $x= \dfrac{7}{1{,}4} = 5$
  Durch Lösen der Gleichung ergibt sich $x = 5$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Löse die Klammern auf, indem du sie ausmultiplizierst.
  Bringe alle Terme mit einem $x$ auf eine Seite.
  Vereinfache den Ausdruck durch Subtraktion und Addition der Terme.
  Teile durch die Zahl die nun vor dem $x$ steht.
2. $7{,}5x+\ \dfrac{6x-2}{4}-9=\dfrac{12x+24}{2}-3{,}5$
  /8
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Grundrechenarten
  Terme auf einen Nenner bringen
  $\dfrac{4 \cdot 7{,}5x+6x-2-9 \cdot 4}{4} = \dfrac{12x+24- 3{,}5 \cdot 2}{2}$
  Auflösen des Nenners
  $2\cdot (30x+6x-2-36) = 4 \cdot (12x+24- 7)$
  Ausmultiplizieren der Klammern
  $60x+12x-4-72 = 48 x+ 96- 28$
  Vereinfachen
  $24x = 144$
  Endergebnis
  $x = \dfrac{144}{24} = 6$
  Durch Lösen der Gleichung ergibt sich $x = 6$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bringe die Terme auf jeder Seite auf einen Nenner.
  Multipliziere mit den Nennern um die Brüche verschwinden zu lassen.
  Multipliziere die Klammern aus.
  Bringe alle Terme mit einem $x$ auf eine Seite.
  Vereinfache den Ausdruck durch Subtraktion und Addition der Terme.
  Teile durch die Zahl die nun vor dem $x$ steht.
2
Die Tabelle zeigt die Entwicklung der durchschnittlichen Kraftstoffpreise in den Jahren 2018 bis 2022.
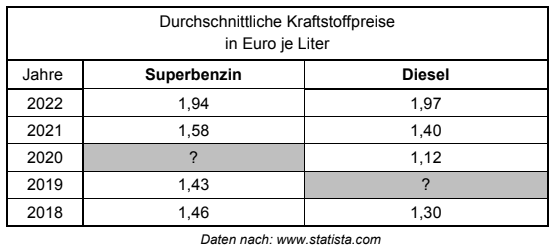
1. Im Jahr 2019 war ein Liter Diesel $11$ % günstiger als ein Liter Superbenzin.
  Berechne den Preis für einen Liter Diesel im Jahr 2019.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Dreisatz
  $100\%≙1{,}43$
  $1\%≙0{,}0143$
  $89\%≙1{,}2727$
  $1{,}2727\approx1{,}27$
  Der Preis für einen Liter Diesel im Jahr 2019 ist ca. $1{,}27$ €.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne den Preis mit Hilfe des Dreisatzes.
  Beachte: Der Preis von einem Liter Diesel beträgt $100\%-11\%=89\%$ vom Preis von einem Liter Superbenzin.
2. Ermittle den Preisanstieg für Superbenzin vom Jahr 2019 bis zum Jahr 2022 in Prozent.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Dreisatz
  $1{,}94\ €-1{,}43\ €=0{,}51€$
  $1{,}43\ €≙100$ %
  $0{,}0143\ €≙1\%$
  $0{,}51\ €≙35{,}66..$ %
  Der Preisanstieg für Superbenzin von 2019 bis 2022 beträgt ca. $35{,}66\%$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne die Differenz der Preise von 2019 und 2022.
  Berechne den Prozentsatz mit Hilfe des Dreisatzes.
3. Der Preis für einen Liter Superbenzin ist vom Jahr 2020 bis zum Jahr 2021 um $22{,}5$ % gestiegen.
  Berechne den Preis für einen Liter Superbenzin im Jahr 2020.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Dreisatz
  $122{,}5\%≙1{,}58$
  $1\%≙0{,}01289..$
  $100\%≙1{,}289...$
  Ein Liter Superbenzin kostete im Jahr 2020 ca. $1{,}29$ €.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne den Preis mit Hilfe des Dreisatzes.
4. Eine Zeitung berichtet: „Der Dieselpreis ist von 2018 bis 2022 stärker gestiegen als der Preis für Superbenzin.“
  Überprüfe, ob diese Aussage stimmt.
  /4
  
  Preisanstieg Diesel von 2018 bis 2022: $1{,}97-1{,}30=0{,}67$
  Preisanstieg Super von 2018 bis 2022: $1{,}94-1{,}46=0{,}48$
  $0{,}67>0{,}48$
  Die Aussage stimmt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3
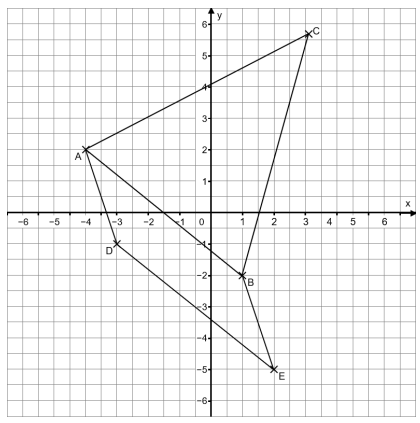
1. Zeichne ein Koordinatensystem (Einheit $1\ cm$ ) und trage die Punkte $A(−4│2)$
  und $B(1│−2)$ ein.
  Hinweis zum Platzbedarf: x-Achse von -6 bis 6, y-Achse von −6 bis 6
2. Verbinde die Punkte $A$ und $B$ zur Strecke $\ \overline{AB}$ . Die Strecke $\overline{AB}$ ist die Basis des gleichschenkligen Dreiecks $ABC$ . Die Schenkellänge beträgt $8\ cm$ .
  Zeichne dieses Dreieck.
3. Zeichne den Punkt $D(−3│−1)$ ein.
  Ergänze den fehlenden Punkt $E$ des Parallelogramms $DEBA$ und gib die
  Koordinaten des Punktes $E$ an.
  /4
4
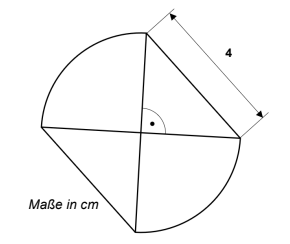
Die abgebildete Figur besteht aus
zwei gleichschenkligen Dreiecken und
zwei Viertelkreisen.
Berechne den Flächeninhalt der Figur.
Hinweis:
Skizze nicht maßstabsgetreu
Quelle: StMUK
/4

Für diese Aufgabe benötigst Du folgendes Grundwissen: Satz des Pythagoras
Berechne Länge der Katheten (Bezeichnung a) bzw. des Radius (Bezeichnung r) mit dem Satz des Pythagoras.
$4^2=a^2+a^2$
$16=2a^2$
$a=\sqrt{8}\approx2{,}83$
$r\approx2{,}83$
Flächeninhalt der beiden rechtwinkligen Dreiecke:
Benutze für die Berechnung einer Dreiecksfläche jeweils eine Kathete als Grundlinie und eine als Höhe.
Dreiecksfläche: $A_{Dreieck}=\frac{1}{2}\cdot a\cdot a$
$\displaystyle A_{Dreiecksflächen}=\dfrac{1}{2}\cdot a\cdot a\cdot 2=a\cdot a\approx8{,}01$
Flächeninhalt der beiden Kreissegmente:
Kreisfläche: $A=r^2\cdot\pi$
$A_{Kreissegmente}=(^{ }r^2\cdot\pi):2=(2{,}83^2\cdot3{,}14):2\approx12{,}57$
Gesamtfläche: $8{,}01+12{,}57=20{,}58$
Die Gesamtfläche der Figur ist $20{,}58\cm^2$ .
5
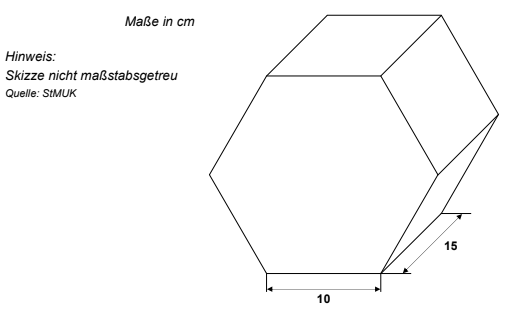
Der abgebildete Körper ist ein sechsseitiges regelmäßiges Prisma.
Berechne das Volumen des Körpers.
/4
Für diese Aufgabe benötigst Du folgendes Grundwissen: Reguläre Vielecke
Flächeninhalt der Grundfläche
Um das Volumen des Körpers zu berechnen, braucht man den Flächeninhalt der Grundfläche, die hier ein regelmäßiges Sechseck ist.
Für regelmäßige Vielecke mit mehr als 4 Ecken gibt es eine Formel, mit der man den Flächeninhalt berechnen kann:
$\text{A} = \dfrac{n \cdot a^2}{4 \cdot \tan \left( \dfrac{180°}{n} \right)}$
$a$ steht hier für die Länge einer Seite des Vielecks, $n$ für die Anzahl der Ecken.
Man setzt also $10$ für $a$ und $6$ für $n$ ein:
$\text{A} = \dfrac{6 \cdot 10^2}{4 \cdot \tan \left( \dfrac{180°}{6} \right)} \approx 259{,}8076211$
Volumen des Körpers
Jetzt multipliziert man den Flächeninhalt der Grundfläche mit der Höhe des Körpers:
$259{,}8076211 \cdot 15 \approx 3897{,}11$
Das Volumen des Körpers beträgt rund $3897{,}11\ \cm^3$ .
Berechne den Flächeninhalt der Grundfläche des Körpers
Multipliziere diesen Flächeninhalt mit der Höhe des Körpers
6
3000 neue Schulbücher müssen in den Keller getragen werden. Jede Person transportiert 150 Bücher pro Stunde.
1. Die Arbeit soll in 4 Stunden erledigt werden.
  Berechne die Anzahl der benötigten Personen.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Indirekte Proportionalität
  Berechne zunächst, wie viele Stunden eine Person für die Arbeit benötigt.
  $\dfrac{3\,000}{150}=20$
  Zwischen der Anzahl der Stunden für die Arbeit und der Anzahl der dafür benötigten Personen liegt eine indirekte Proportionalität vor.
  $20\cdot 1=4\cdot 5$
  Wenn eine Person $20$ Stunden benötigt, dann schaffen $5$ Personen die Arbeit in $4$ Stunden.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne, wie lange eine Person für die Arbeit benötigt
  Berechne daraus die Anzahl der Personen, die die Arbeit in $4$ Stunden schaffen. Beachte dabei, dass die Werte zueinander proportional sind.
2. Ermittle mit Hilfe des
  abgebildeten Graphen,
  von wie vielen Personen
  die Arbeit hier erledigt
  wird.
  
  Bücher pro Stunde
  $\dfrac{3000}{2}=1500$
  Anzahl benötigter Personen
  $\dfrac{1500}{150}=10$
  Es werden $10$ Personen benötigt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Lies aus dem Graphen ab oder berechne, wie viele Bücher pro Stunde geschafft werden.
  Berechne die Anzahl benötigter Personen
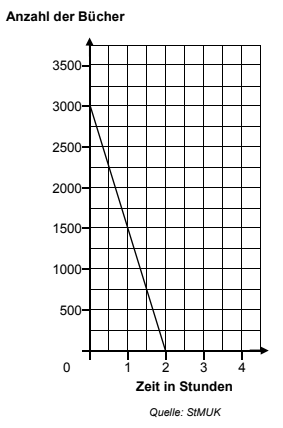
3. Notiere auf deinem Blatt die Buchstaben der korrekten Aussagen zum
  abgebildeten Graphen.
  $A$ Nach einer Stunde ist die Hälfte der Arbeit erledigt.
  $B$ Nach $1\ ⁄\ 2$ Stunde sind noch $750$ Bücher übrig.
  $C$ In einer Stunde werden $1000$ Bücher transportiert.
  $D$ Nach zwei Stunden sind $3000$ Bücher transportiert.
  
  Aussage $A$
  Ausgehend von der $1$ auf der x-Achse, stellst du fest, dass nach einer Stunde $1\,500$ Bücher geschafft sind. Dies ist genau die Hälfte der Arbeit.
  Aussagen $A$ ist korrekt.
  Aussage $B$
  Ausgehend von $0{,}5$ auf der x-Achse, stellst du fest, dass nach einer halben Stunde erst $750$ Bücher geschafft sind. $3\,000-750=2\,250$ Bücher sind noch übrig.
  Aussage $B$ ist falsch.
  Aussage $C$
  Ausgehend von der $1$ auf der x-Achse, stellst du fest, dass nach einer Stunde $1\,500$ Bücher geschafft sind.
  Aussage $C$ ist falsch.
  Aussage $D$
  Ausgehend von der $2$ auf der x-Achse, stellst du fest, dass nach zwei Stunden $3\,000$ Bücher geschafft sind.
  Aussage $D$ ist korrekt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Überprüfe die Aussagen anhand des Graphen
4. 6 Schülerinnen und Schüler bieten ihre Hilfe an.
  Berechne, wie viele Bücher sie in 3 Stunden transportieren könnten.
  /4
  
  Multipliziere
  $\text{Anzahl Schülerinnen\,}\cdot\text{\,Bücher pro Person pro Stunde\,}\cdot\text{\,Anzahl Stunden}$
  $6\cdot150\cdot3=2\,700$
  $6$ Schülerinnen transportieren in $3$ Stunden $2\,700$ Bücher.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
7
Anna würfelt mehrfach mit einem sechsseitigen Spielwürfel.
Mit Hilfe einer Strichliste wurden die Ergebnisse festgehalten.
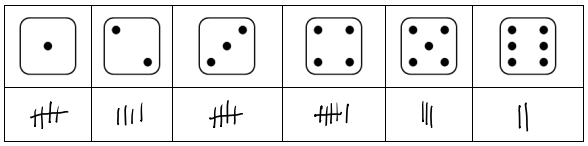
1. Ermittle die relative Häufigkeit in Prozent, mit der Anna eine 2 gewürfelt hat.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Relative Häufigkeit
  Gesamtanzahl der Würfe
  Addiere die Anzahl der Striche der einzelnen Versuche
  $5+4+5+6+3+2=25$
  Relative Häufigkeit für eine $2$
  Die relative Häufigkeit $h_n$ für ein Ereignis $n$ berechnet man mit der Formel
  $h_n=\dfrac{\text{absolute Häufigkeit\,} H_n}{\text{Anzahl der Versuche\,} n}$
  $h_n=\dfrac{4}{25}=0{,}16=16\%$
  x
  Die relative Häufigkeit, mit der Anna eine $2$ gewürfelt hat, beträgt $16\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Errechne die Gesamtanzahl der Würfe
  Berechne die relative Häufigkeit
2. Anna würfelt noch ein weiteres Mal.
  Bestimme die Wahrscheinlichkeit in Bruch- und Prozentschreibweise, mit der
  sie eine Zahl größer als $4$ erhält.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeit
  Die Wahrscheinlichkeit für jede Zahl eines Würfels beträgt $\frac{1}{6}$ .
  Wahrscheinlichkeit $P(5;6)$
  Die Wahrscheinlichkeit, eine Zahl größer als $4$ zu würfeln, ist gleich der Wahrscheinlichkeit, eine $5$ oder eine $6$ zu würfeln.
  $P(5;6)=P(5)+P(6)=\dfrac{1}{6}+\dfrac{1}{6}=\dfrac{2}{6}=\dfrac{1}{3}$
  Prozentschreibweise
  $\dfrac{1}{3}=0,\overline{3}=33{,}33\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Beschreibe die Ereignismenge $E=\left\{2;4;6\right\}$ bei einmaligem Würfeln in Worten.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeit
  $E=\{2;4;6\}$ bedeutet:
  Es wird eine $2$ , eine $4$ oder eine $6$ gewürfelt.
  oder
  Es wird eine gerade Zahl gewürfelt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. Anna behauptet: „Wenn ich $1000$ Mal würfle, ist zu erwarten, dass die Augenzahl $6$ etwa $250$ Mal erscheint.“
  Entscheide, ob Anna recht hat und begründe rechnerisch.
  /4
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeit
  Die Wahrscheinlichkeit für eine $6$ beträgt $\dfrac{1}{6}$
  Wahrscheinlichkeit für eine $6$ bei $1\,000$ Würfen
  Bei $1\,000$ Würfen ist zu erwarten, dass $1\,000\cdot\dfrac{1}{6}=\dfrac{1\,000}{6}\approx 166{,}66$ Würfe eine $6$ ergeben.
  Vergleich
  $166{,}66<250$
  Anna hat nicht recht.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne die Wahrscheinlichkeit für eine $6$ bei $1\,000$ Würfen.
  Vergleiche mit Annas Behauptung