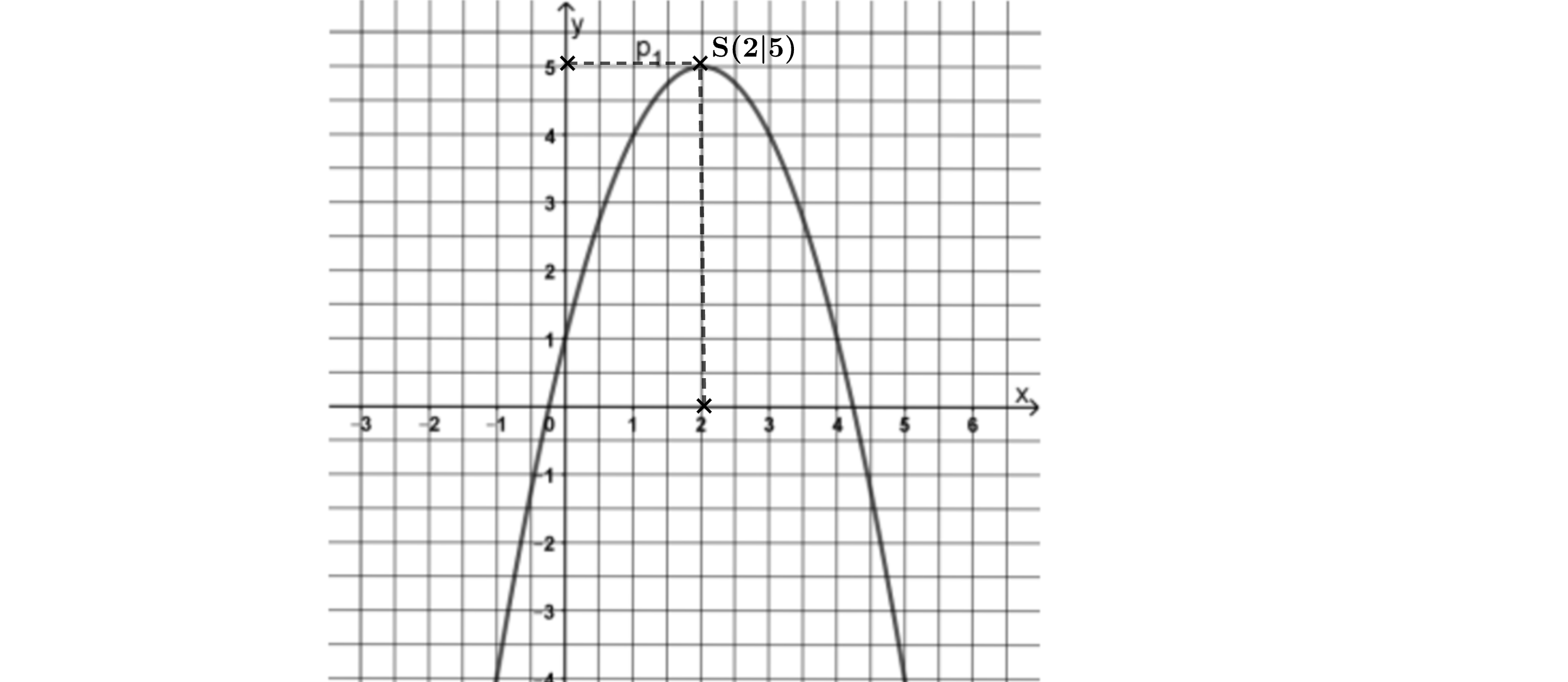
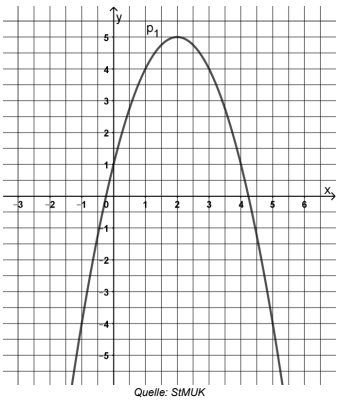
Die nachfolgende Abbildung zeigt die Parabel
Ermitteln Sie rechnerisch die Funktionsgleichung von in der Normalform.
Die Parabel wird an der -Achse gespiegelt.
Geben Sie die Funktionsgleichung dieser gespiegelten Parabel in der
Scheitelpunktform an.
Die Parabel schneidet die -Achse in den Punkten
und .
Berechnen Sie die -Koordinaten dieser beiden Punkte.
Überprüfen Sie rechnerisch, ob die Punkte und auf der
Parabel liegen.
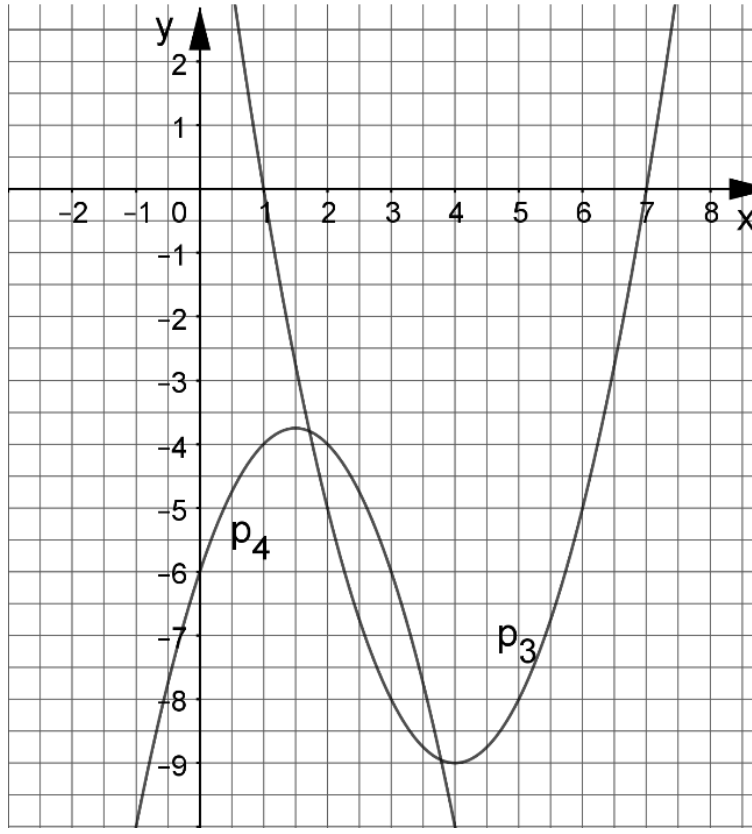
Die Gerade schneidet die Parabel in den
Punkten und .
Ermitteln Sie rechnerisch die Koordinaten dieser Schnittpunkte und geben
Sie und an.
Zeichnen Sie die Parabeln und in ein Koordinatensystem mit der
Längeneinheit .
/7
WICHTIG: Damit alle Bilder und Formeln gedruckt werden, scrolle bitte einmal bis zum Ende der Seite BEVOR du diesen Dialog öffnest. Vielen Dank!
🎓 Ui, schon Prüfungszeit? Hier geht's zur Mathe-Prüfungsvorbereitung.