Wahlteil
🎓 Prüfungsbereich für Niedersachsen
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
- 1
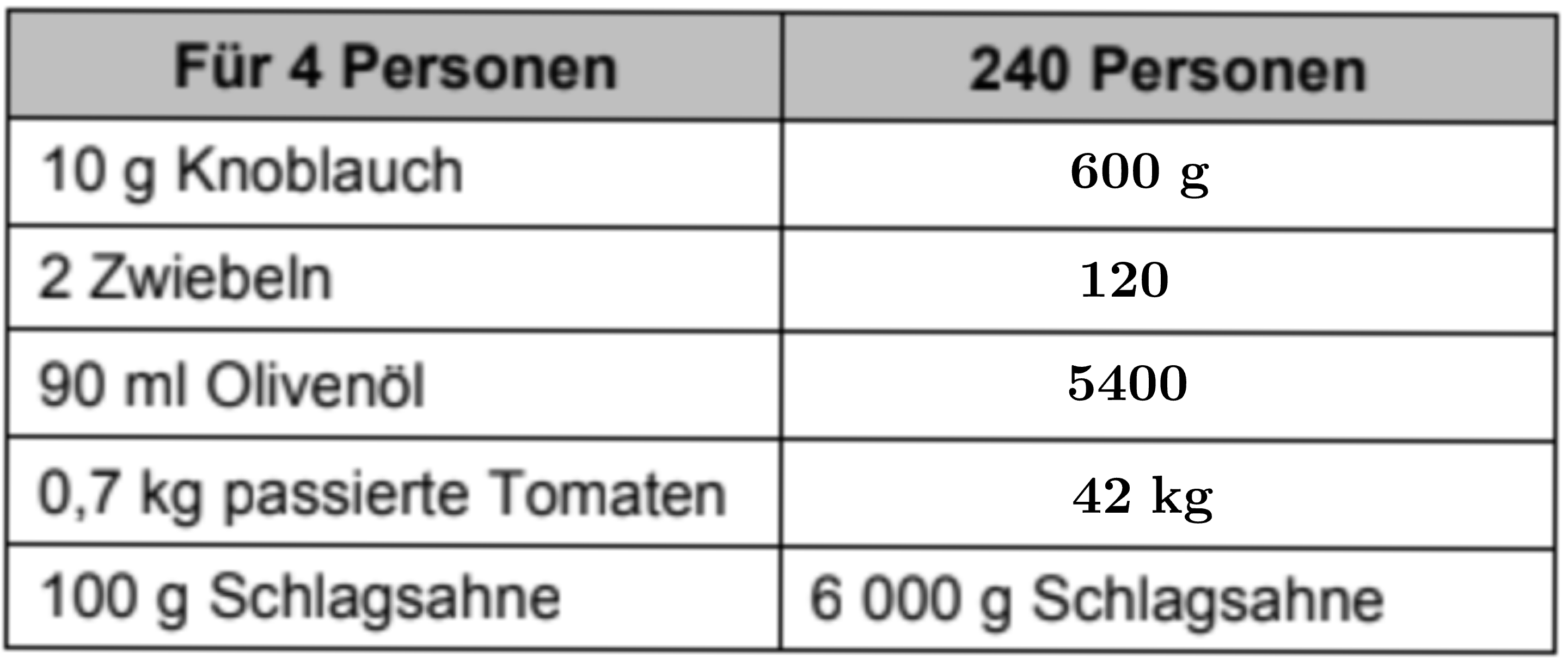
Die Schülerfirma „Good food“ möchte für das Schulfest eine Suppe kochen. Das Rezept ist für 4 Personen.
Berechne die Zutaten für 240 Personen.
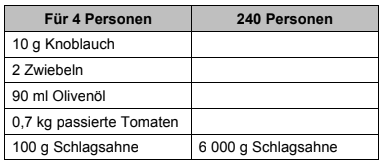
[ 2 Pkte ]
Die Suppe wird in einem großen Topf gekocht.
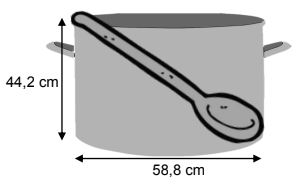
Berechne das Volumen des abgebildeten Topfes in Litern (l).
Hinweis: 1 Liter (l)
[ 3 Pkte ]
Michel benötigt einen Kochlöffel für den Topf.
Berechne, wie lang der Kochlöffel mindestens sein muss, damit er immer bis oben an den Rand reicht.
[ 2 Pkte ]
Nach dem Essen bleiben 10 Liter () Suppe übrig.
Berechne die Füllhöhe () der Suppe im Topf.
[ 2 Pkte ]
Das Volumen und der Radius eines Zylinders sind gegeben.
Gib eine allgemeine Formel zur Berechnung der Körperhöhe an.
[ 1 Pkt ]
- 2
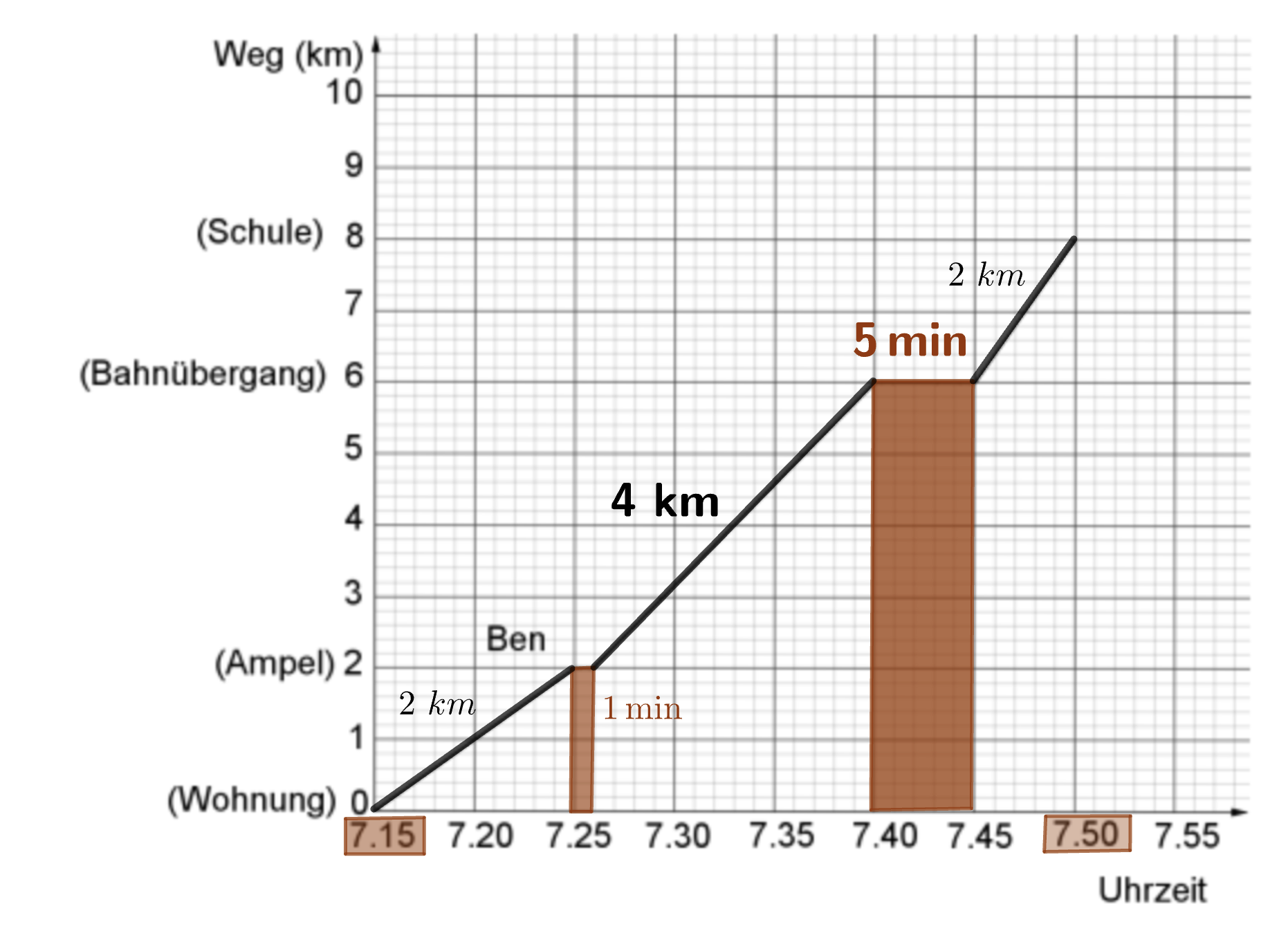
Ben fährt mit dem Fahrrad zur Schule. Sein Schulweg wird durch den folgenden Graphen dargestellt.
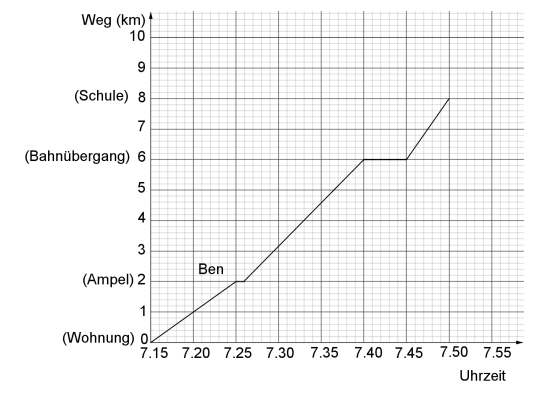
Ergänze den Lückentext.
Ben fährt um __________ Uhr mit dem Fahrrad von zu Hause aus los.
Die Strecke von der Ampel bis zum Bahnübergang ist __________ km lang.
Am Bahnübergang muss Ben __________ Minuten warten.
Insgesamt benötigt Ben für seinen Schulweg __________ Minuten.
[ 2 Pkte ]
Ben fährt vom Bahnübergang bis zur Schule sehr schnell.
Berechne, wie viele Meter er in der Minute zurücklegt.
[ 2 Pkte ]
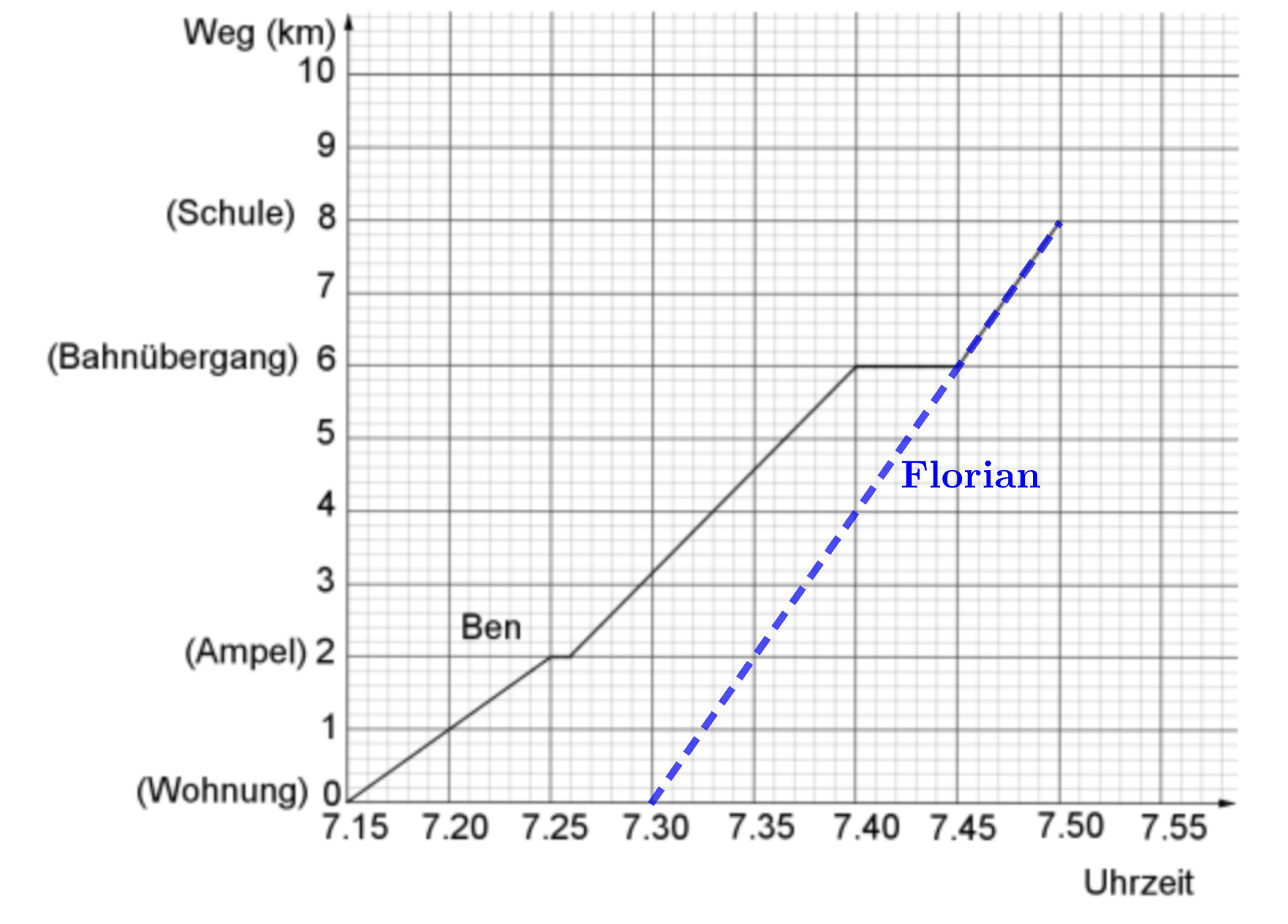
Florian fährt mit dem Fahrrad mit gleichbleibender Geschwindigkeit die gleiche Strecke zur Schule. Er fährt um 7.30 Uhr von der Wohnung aus los. Um 7.50 Uhr erreicht er die Schule.
Zeichne Florians Schulweg in das Koordinatensystem ein.
[ 1 Pkt ]
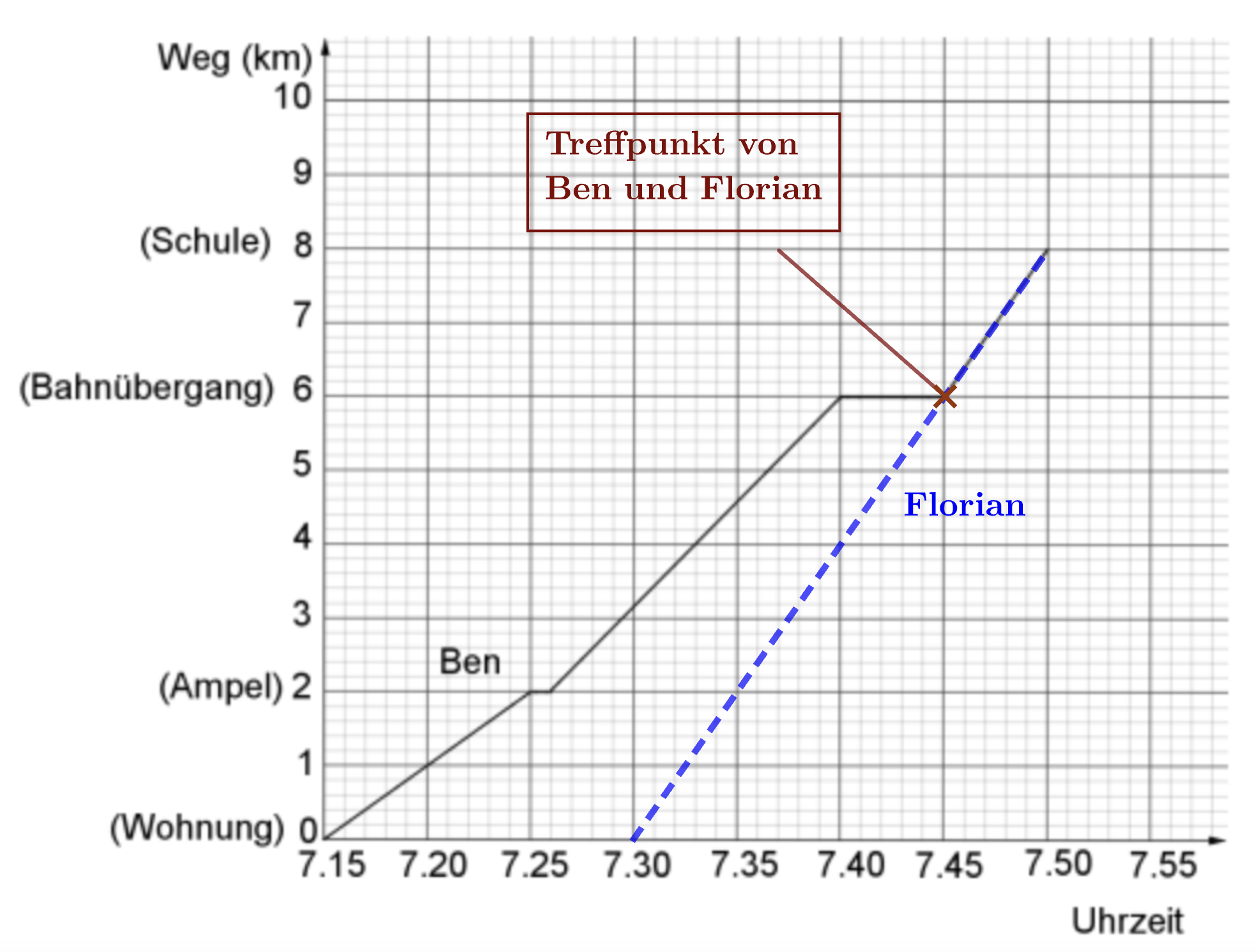
Gib an, um wie viel Uhr Florian und Ben sich treffen.
[ 1 Pkt ]
Ben möchte mit dem E-Bike seines Vaters zur Schule fahren. Er fährt mit einer gleichbleibenden Geschwindigkeit von 24 km pro Stunde.
Ben behauptet: „Wenn ich an der Ampel und am Bahnübergang nicht warten muss, benötige ich für den 8 km langen Schulweg nur 15 Minuten“.
Hat Ben Recht? Kreuze an und begründe.
[ 2 Pkte ]
Ben hat im Schuljahr Schultage. Die Strecke zur Schule und zurück ist insgesamt lang. Die Stromkosten betragen Cent pro .
Berechne, wie hoch die Stromkosten des E-Bikes pro Schuljahr in Euro sind.
- 3
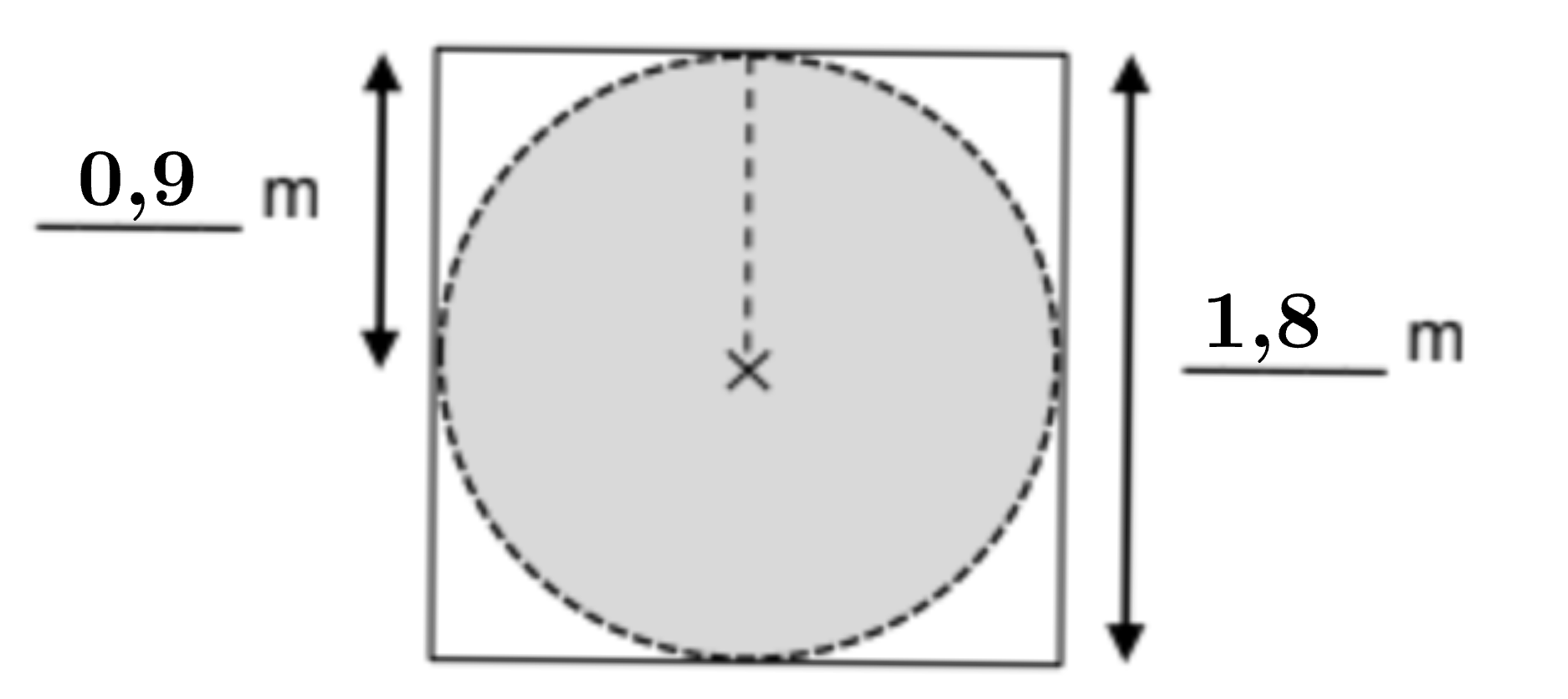
Eine Tischlerei plant die Abdeckung eines Brunnens. Der kreisförmige
Brunnen hat außen einen Durchmesser von . Er soll mit einer Holzplatte abgedeckt werden, die genau mit dem Brunnenrand abschließt. Sie wird aus einer quadratischen Holzplatte ausgesägt.

Ergänze die fehlenden Maße in der Skizze und berechne den Flächeninhalt des kreisrunden Brunnendeckels.
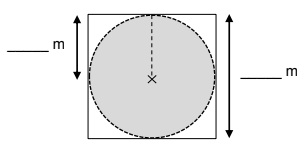
[ 3 Pkte ]
Berechne, wie viel Holz von der quadratischen Platte übrig bleiben.
(Solltest du Teilaufgabe a) nicht gelöst haben, rechne mit weiter.)
[ 3 Pkte ]
Ein Kunde behauptet:
„Wenn der Durchmesser des Brunnens doppelt so groß ist, muss ein Deckel mit doppelt so großem Flächeninhalt angefertigt werden.“
Ist die Aussage wahr oder falsch? Kreuze an und begründe.
[ 2 Pkte ]
Der Kunde erhält eine Rechnung über €. Bei Überweisung innerhalb einer Woche können % Skonto abgezogen werden.
Berechne den Überweisungsbetrag bei Zahlung innerhalb einer Woche.
[ 2 Pkte ]
- 4
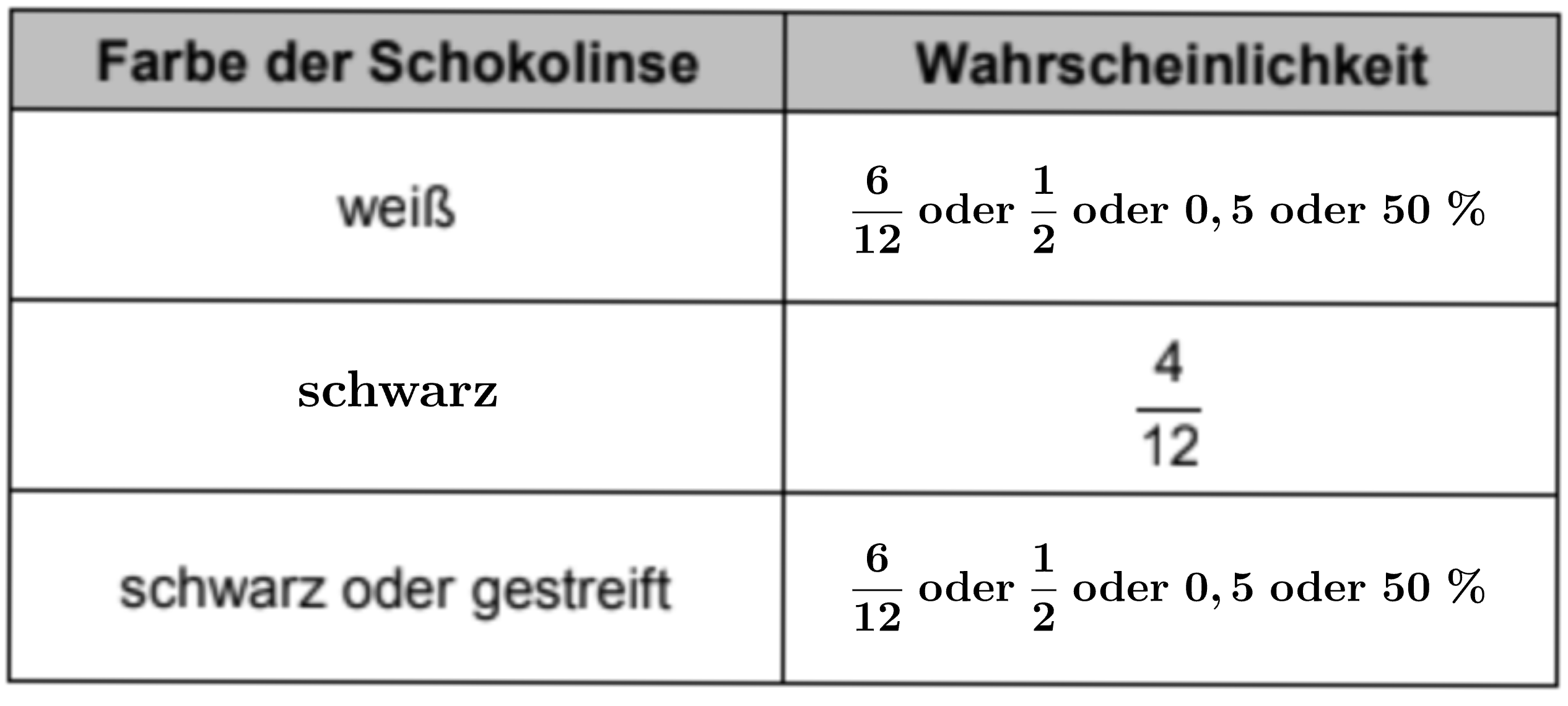
Nina hat eine Schachtel mit schwarzen, weißen und gestreiften Schokolinsen.
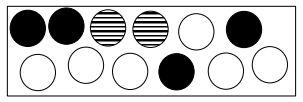
Ergänze die fehlenden Anteile und Farben in der Tabelle.
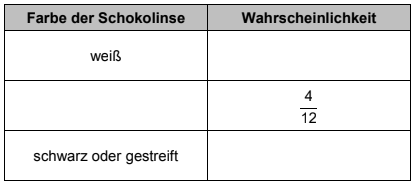
[ 3 Pkte ]
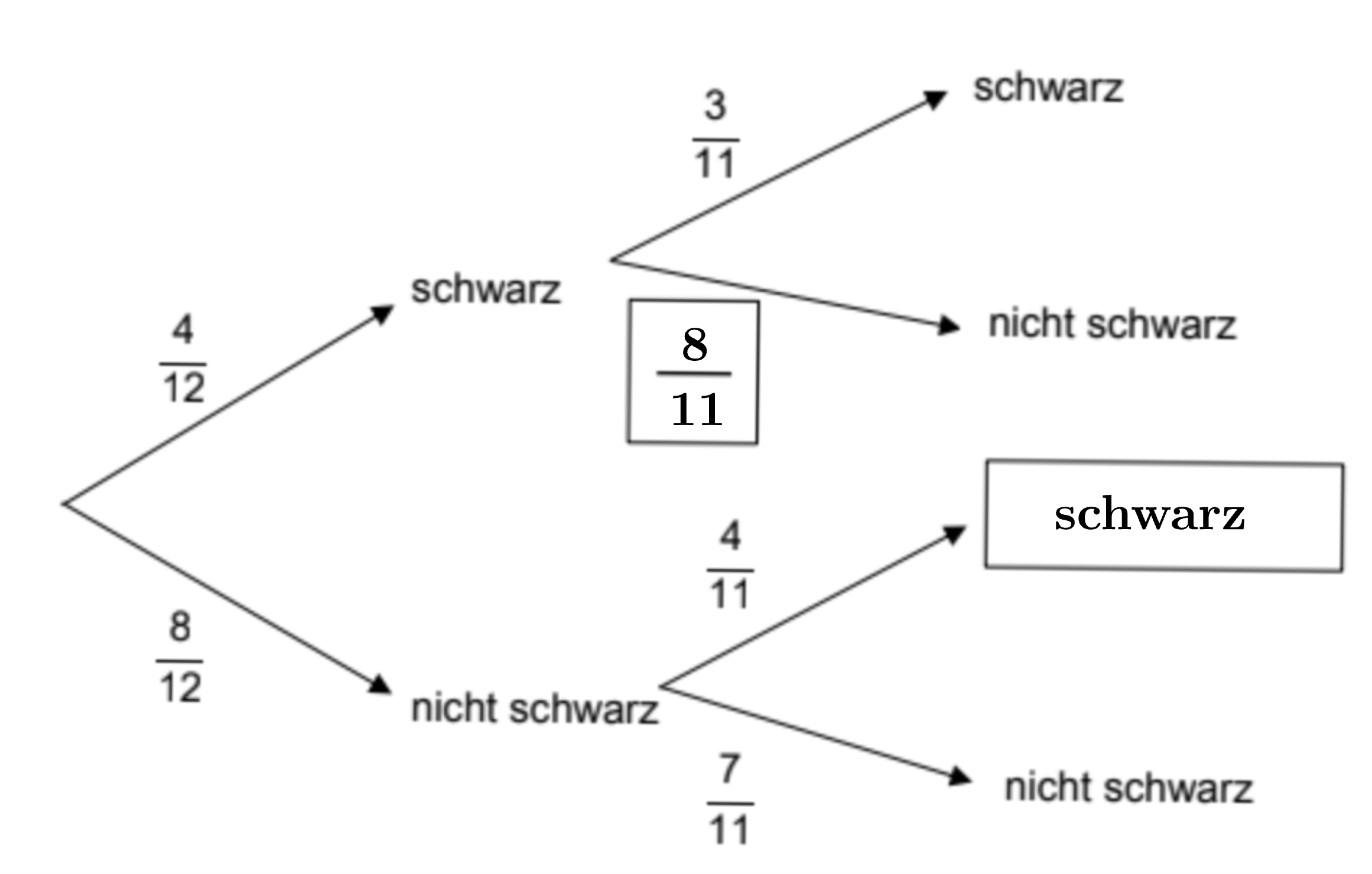
Nina nimmt sich aus ihrer Schachtel zwei Schokolinsen.
Ergänze das Baumdiagramm.
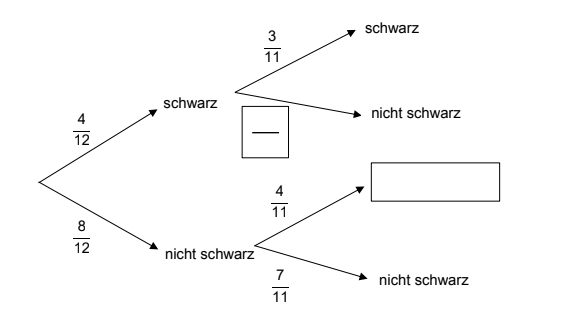
[ 2 Pkte ]
Nina isst gerne schwarze Schokolinsen.
Berechne die Wahrscheinlichkeit, dass nacheinander zwei schwarze Schokolinsen gezogen werden.
[ 2 Pkte ]
Kevin hat eine Schachtel mit schwarzen und weißen Schokolinsen.
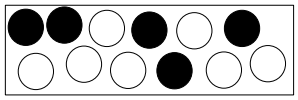
Kreuze an, bei wem die Wahrscheinlichkeit größer ist, eine weiße Schokolinse zu ziehen. Begründe.
[ 2 Pkte ]
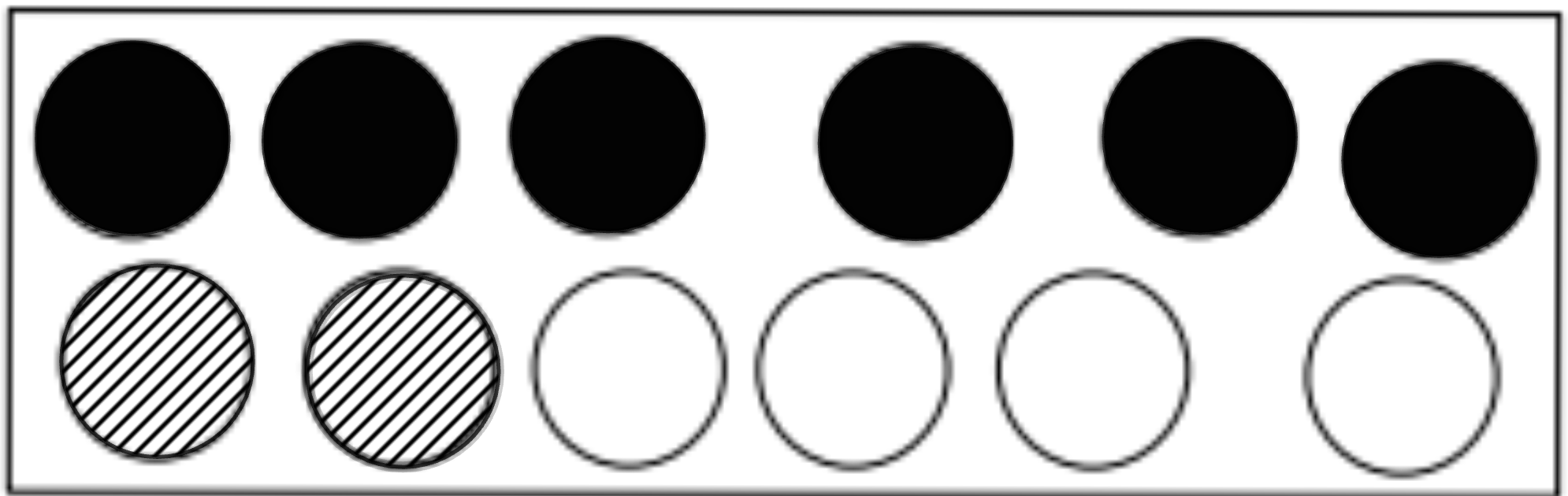
In einer anderen Schachtel befinden sich 12 Schokolinsen mit folgender Verteilung:
weiß schwarz gestreift
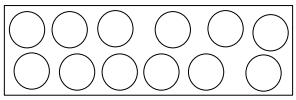
[ 1 Pkt ]
Male die Schokolinsen passend zu der Verteilung an.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?