B2
🎓 Prüfungsbereich für Nordrhein-Westfalen
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
- 1
Aufgabe 1
Auf einer Autobahn entsteht morgens an einer Baustelle häufig ein Stau.
An einem bestimmten Tag entsteht der Stau um 06:00 Uhr und löst sich bis 10:00 Uhr vollständig auf. Für diesen Tag kann die momentane Änderungsrate der Staulänge von der Entstehung bis zur Auflösung des Staus mithilfe der in definierten Funktion mit
beschrieben werden.
Dabei gibt die nach 06:00 Uhr vergangene Zeit in Stunden und die momentane Änderungsrate der Staulänge in Kilometer pro Stunde an.
Nennen Sie die Zeitpunkte, zu denen die momentane Änderungsrate der Staulänge den Wert null hat, und begründen Sie anhand der Struktur des Funktionsterms von , dass es keine weiteren solcher Zeitpunkte gibt. (3 P)
Es gilt .
Geben Sie die Bedeutung dieser Tatsache im Sachzusammenhang an. (1 P)
Bestimmen Sie den Zeitpunkt, zu dem die Staulänge am stärksten zunimmt. (2 P)
Zeigen Sie, dass der zugehörige Wert der momentanen Änderungsrate zwischen und liegt. (1 P)
Geben Sie den Zeitpunkt an, zu dem der Stau am längsten ist. Begründen Sie Ihre Angabe. (2 P)
Im Sachzusammenhang ist neben der Funktion die in definierte Funktion mit
von Bedeutung.
Begründen Sie, dass die folgende Aussage richtig ist:
Die Staulänge in Kilometern kann für jeden Zeitpunkt von 06:00 Uhr bis 10:00 Uhr durch die Funktion angegeben werden.
Bestätigen Sie rechnerisch, dass sich der Stau um 10:00 Uhr vollständig aufgelöst hat. (4 P)
Berechnen Sie die Zunahme der Staulänge von 06:30 Uhr bis 08:00 Uhr und bestimmen Sie für diesen Zeitraum die durchschnittliche Änderungsrate der Staulänge. (3 P)
Bestimmen Sie denjenigen Zeitpunkt zwischen 06:00 Uhr und 10:00 Uhr, zu dem die Staulänge km geringer ist als eine Stunde vorher. (3 P)
Für einen anderen Tag wird die momentane Änderungsrate der Staulänge für den Zeitraum von 06:00 Uhr bis 10:00 Uhr durch den in der Abbildung 1 gezeigten Graphen dargestellt. Dabei ist die nach 06:00 Uhr vergangene Zeit in Stunden und die momentane Änderungsrate in Kilometer pro Stunde.
Um 07:30 Uhr hat der Stau eine bestimmte Länge. Es gibt einen anderen Zeitpunkt, zu dem der Stau die gleiche Länge hat.
Markieren Sie diesen Zeitpunkt näherungsweise in Abbildung 1 und begründen Sie Ihr Vorgehen. (3 P)
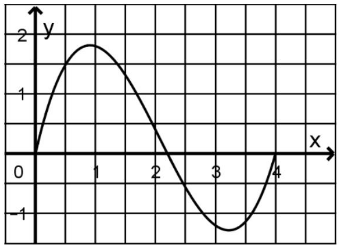
Abbildung 1
- 2
Aufgabe 2
Die Aufgabe 2 ist eine Fortsetzung der Aufgabe 1.
Betrachtet wird die Schar der in definierten Funktionen mit
Es gilt: .
Bestimmen Sie die lokalen Extremstellen von und die Art dieser Extremstellen in Abhängigkeit von . (6 P)
[Zur Kontrolle: Der einzige lokale Hochpunkt des Graphen von befindet sich an der Stelle .]
Eine Verkehrszentrale überwacht den Autobahnverkehr in der Umgebung. Die Computersysteme der Verkehrszentrale erhalten ständig Daten von Sensoren und Kameras, die von einer Software verarbeitet werden.
Die Software modelliert Staulängen mit den Funktionen . Dabei gibt mit die vergangene Zeit in Stunden ab der Entstehung des Staus und die Staulänge in Kilometer an.
Auf einem Display wird ein Stau angezeigt, der um 06:00 Uhr entstanden ist.
Für die Modellierung dieses Staus verwendet die Software die Parameter und .
Berechnen Sie den Zeitpunkt, zu dem die vorhergesagte Staulänge erstmals nach der Entstehung Kilometer beträgt. (2 P)
Um 06:40 Uhr schaltet eine Mitarbeiterin der Verkehrszentrale eine Reihe von computergesteuerten Verkehrszeichen - ein sogenanntes Leitsystem - ein, die bei der Reduzierung des Staus helfen sollen. Dadurch ändern sich die Parameter der Modellierung für die Zeit nach 06:40 Uhr auf und .
Berechnen Sie, um wie viel Prozent die vorausgesagte maximale Staulänge durch das Einschalten des Leitsystems reduziert wird. (4 P)
Zusätzlich zum Leitsystem soll ein Polizeieinsatz bei der Reduzierung des Staus helfen. Die Polizei will dafür sorgen, dass die Staulänge ab 11:00 Uhr konstant mit der Änderungsrate abnimmt, die die Software für 11:00 Uhr vorhersagt.
(i) Ermitteln Sie unter diesen Voraussetzungen grafisch anhand von Abbildung 2, wann sich der Stau aufgelöst haben wird. (2 P)
(ii) Überprüfen Sie Ihr Ergebnis aus (i) durch eine geeignete Rechnung. (4 P)
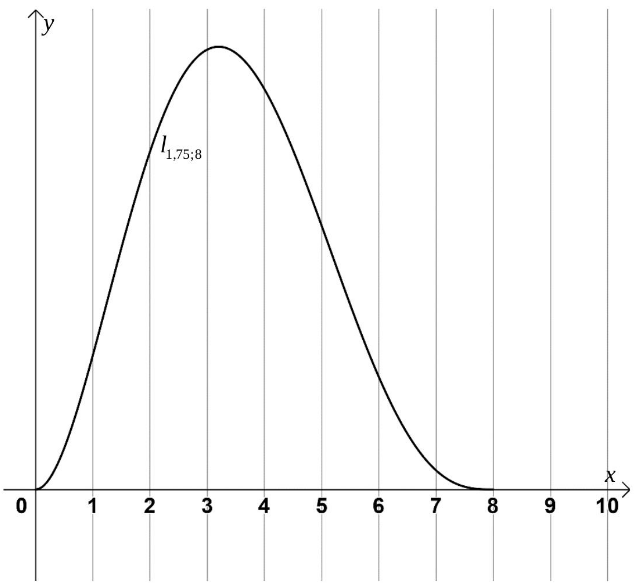
Abbildung 2
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?


