A2

🎓 Prüfungsbereich für Nordrhein-Westfalen

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

1
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 1
Gegeben ist eine in $\mathbb{R}$ definierte Funktion $f(x)=x^4-k\cdot x^2$ , wobei $k$ eine positive reelle Zahl ist. Abbildung 1 zeigt den Graphen von $f$ .
Abbildung 1
1. Zeigen Sie, dass $f'(x)=2x\cdot(2x^2-k)$ eine Gleichung der ersten Ableitungsfunktion von $f$ ist. (1 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
  Zeige, dass $f'(x)=2x\cdot(2x^2-k)$ eine Gleichung der ersten Ableitungsfunktion von $f$ ist
  Gegeben ist $f(x)=x^4-k\cdot x^2$ .
  Dann ist $f'(x)=4\cdot x^3-2\cdot k \cdot x=2x\cdot(2x^2-k)$ .
  Es ist also $f'(x)=2x\cdot(2x^2-k)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Leite $f (x)$ ab.
2. Die beiden Tiefpunkte des Graphen von $f$ haben jeweils die y-Koordinate $- 1$ .
  Ermitteln Sie den Wert von $k$ . (4 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremum
  Ermittele den Wert von $k$
  Es ist $f'(x)=2x\cdot(2x^2-k)$ .
  Die notwendige Bedingung für ein Extremum lautet $f^{'} (x) = 0$ .
  $\Rightarrow\;0=2x\cdot(2x^2-k)$
  Mit dem Satz vom Nullprodukt folgt:
  $x=0\vee x=\pm\sqrt{\dfrac{k}{2}}$
  Die beiden Tiefpunkte des Graphen von $f$ haben jeweils die y-Koordinate $- 1$ , d.h. auf die hinreichende Bedingung kann verzichtet werden.
  Zu den beiden Tiefpunkte gehören die Extremstellen $x=\pm\sqrt{\dfrac{k}{2}}$ .
  Für $k > 0$ gilt: $f\left(\sqrt{\dfrac{k}{2}}\right)=-1\;\Rightarrow\;\left(\sqrt{\dfrac{k}{2}}\right)^4-k\cdot \left(\sqrt{\dfrac{k}{2}}\right)^2=-1$
  $\Rightarrow\;\dfrac{k^2}{4}-\dfrac{k^2}{2}=-1\;\Rightarrow\;-\dfrac{k^2}{4}=-1\Rightarrow\;k^2=4\;\Rightarrow\; k=2$ .
  Der gesuchte Wert von $k$ ist $k = 2$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Die notwendige Bedingung für ein Extremum lautet $f^{'} (x) = 0$ .
  Bestimme die Extremstellen $x_{E}$ .
  Die Tiefpunkte liegen nicht bei $x = 0$ .
  Löse die Gleichung $f (x_{E}) = - 1$ nach $k$ auf. Beachte $k > 0$ .
2
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 2
Die Funktion $f$ ist gegeben durch $f(x)=-x^3+9x^2-23x+15, x \in \mathbb{R}$ .
Die Funktion $F$ ist eine Stammfunktion zur Funktion $f$ .
Der Graph von $f$ ist in Abbildung 2 dargestellt.
Abbildung 2
1. Interpretieren Sie die Aussage $F (5) - F (1) = 0$ in Bezug auf den Graphen von $f$ .
  (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
  Interpretiere die Aussage $F (5) - F (1) = 0$ in Bezug auf den Graphen von $f$
  Die Fläche, die im Intervall $[1; 3]$ vom Graphen von $f$ und der x-Achse eingeschlossen wird, ist genauso groß wie die Fläche, die im Intervall $[3; 5]$ vom Graphen von $f$ und der x-Achse eingeschlossen wird
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Betrachte die Flächen unterhalb und oberhalb der x-Achse.
2. Berechnen Sie $\displaystyle\int_0^1 f(x)\;\mathrm{d}x$ . (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktion
  Berechne $\displaystyle\int_0^1 f(x)\;\mathrm{d}x$
  Es ist $f (x) = - x^{3} + 9 x^{2} - 23 x + 15$ .
  Dann ist $F(x)=-\dfrac{1}{4}x^4+3x^3-\dfrac{23}{2}x+15x$ eine Stammfunktion von $f$ .
  $\displaystyle\int_0^1 f(x)\;\mathrm{d}x=F(1)-F(0)=\left(-\dfrac{1}{4}+3-\dfrac{23}{2}+15\right)-(0)=18-\dfrac{47}{4}=\dfrac{25}{4}$
  Ergebnis: $\displaystyle\int_0^1 f(x)\;\mathrm{d}x=\dfrac{25}{4}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Ermittele eine Stammfunktion von $f$ .
  Berechne $\displaystyle\int_0^1 f(x)\;\mathrm{d}x=F(1)-F(0)$ .
3
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 3
Gegeben ist die Funktion $f$ mit $f(x)=\left(x^{2}+2 x\right) \cdot \mathrm{e}^{-x+4}$ mit $x \in \mathbb{R}$ .
Der Graph von $f$ ist in Abbildung 3 dargestellt.
Abbildung 3
1. Die Funktion $f$ besitzt genau zwei Extremstellen.
  Ermitteln Sie die beiden Extremstellen von $f$ .
  $[$ Hinweis: Ein Nachweis der hinreichenden Bedingung ist nicht erforderlich. $]$ (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen
  Ermittle die beiden Extremstellen von $f$ .
  Berechne die 1. Ableitung:
  $f'(x)=(2x+2)\cdot e^{-x+4}+\left(x^{2}+2 x\right) \cdot \mathrm{e}^{-x+4}\cdot (-1)=(-x^2+2)\cdot\mathrm{e}^{-x+4}$ .
  Die notwendige Bedingung ist $f^{'} (x) = 0$ .
  $\Rightarrow\;0=(-x^2+2)\cdot\mathrm{e}^{-x+4}$
  Wegen $\mathrm{e}^{-x+4}\neq 0$ für alle $x\in \mathbb{R}$ ist $- x^{2} + 2 = 0$ .
  $\Rightarrow\;x=-\sqrt{2}\vee x=\sqrt{2}$
  Da die Funktion $f$ genau zwei Extremstellen besitzt, sind die beiden Extremstellen $x=-\sqrt{2}$ und $x=\sqrt{2}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne die 1. Ableitung.
  Die notwendige Bedingung ist $f^{'} (x) = 0$ . Löse die Gleichung nach $x$ auf.
2. Skizzieren Sie in Abbildung 3 den Graphen der ersten Ableitungsfunktion von $f$ .
  $[$ Hinweis: Die Größe der $y$ -Werte kann dabei unberücksichtigt bleiben. $]$ (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Graph einer Funktion
  Graphen von $f$ und von $f^{'}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 4
Für jedes $a \in \mathbb{R}$ ist durch die Gleichung $f_{a}(x)=\frac{1}{2}(x+2)(3 x+a)^{2} \mathrm{e}^{x}, x \in \mathbb{R}$ , eine Funktion $f_{a}$ gegeben.
In Abbildung 4 ist der Graph der Funktion $f_{a}$ für $a = 0$ abgebildet.
Abbildung 4
1. Es gibt genau einen Wert von $a$ , sodass die Funktion $f_{a}$ nur eine Nullstelle besitzt.
  Ermitteln Sie diesen Wert von $a$ . (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstelle
  Ermittle diesen Wert von $a$
  Gegeben ist $f_{a}(x)=\frac{1}{2}(x+2)(3 x+a)^{2} \mathrm{e}^{x}$ .
  Berechne die Nullstellen:
  Löse die Gleichung $f (x) = 0$ :
  $0=\frac{1}{2}(x+2)(3 x+a)^{2} \mathrm{e}^{x}$
  Wegen $\mathrm{e}^{x}\neq 0$ für alle $x\in \mathbb{R}$ ist $x + 2 = 0$ oder $(3 x + a)^{2} = 0$ (Satz vom Nullprodukt).
  $\Rightarrow\;x=-2\vee x=-\dfrac{a}{3}$
  Die Funktion $f_{a}$ darf nur eine Nullstelle besitzen, d.h. $-\dfrac{a}{3}=-2\;\Rightarrow\;a=6$ .
  Für $a = 6$ hat der Graph von $f_{6} (x)$ nur eine Nullstelle.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne die Nullstellen, d.h. löse die Gleichung $f (x) = 0$ $\;\Rightarrow\;x_1$ und $x_{2}$ .
  Die Funktion $f_{a}$ darf nur eine Nullstelle besitzen $\;\Rightarrow\;x_1=x_2$ .
  Löse diese Gleichung nach $a$ auf.
2. Ermitteln Sie, für welche Werte von $a$ der Punkt $P\left(3 \mid 90 \mathrm{e}^{3}\right)$ auf dem Graphen der Funktion $f_{a}$ liegt. (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionswert
  Gegeben ist der Punkt $P\left(3 \mid 90 \mathrm{e}^{3}\right)$ .
  $\Rightarrow\; 90 \mathrm{e}^{3}=\frac{1}{2}(3+2)(3 \cdot 3+a)^{2} \mathrm{e}^{3}=\dfrac{1}{2}\cdot 5\cdot(9+a^2)\cdot\mathrm{e}^{3}$
  Der Koeffizientenvergleich liefert die Gleichung $90=\dfrac{1}{2}\cdot 5\cdot(9+a^2)$ .
  $\Rightarrow\;36=(9+a)^2\;\Rightarrow\;a_{1{,}2}=-9\pm 6\;\Rightarrow\; a=-15\vee a=-3$
  Für $a = - 15$ oder $a = - 3$ liegt der Punkt $P$ auf dem Graphen der Funktion $f_{a}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Setze die Koordinaten des Punktes $P$ in $f_{a} (x)$ ein und löse die Gleichung nach $a$ auf.
5
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 5
Die Zufallsgröße $X$ ist binomialverteilt mit den Parametern $n = 100$ und $p$ .
Der Erwartungswert von $X$ ist 50.
1. Berechnen Sie die Standardabweichung von $X$ . (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Standardabweichung
  Berechne die Standardabweichung von $X$
  Gegeben: Der Erwartungswert von $X$ ist $50$ und $n = 100$ .
  Mit diesen Angaben kann zunächst $p$ berechnet werden:
  $\mu=n\cdot p\;\Rightarrow\;p=\dfrac{\mu}{n}=\dfrac{50}{100}=\dfrac{1}{2}$ .
  Für die Standardabweichung $\sigma$ gilt:
  $\sigma=\sqrt{n\cdot p\cdot (1-p)}=\sqrt{100\cdot \dfrac{1}{2}\cdot \dfrac{1}{2}}=\sqrt{25}=5$
  Die Standardabweichung von $X$ ist $\sigma=5$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Gegeben: Der Erwartungswert von $X$ ist $50$ und $n = 100$ .
  Mit diesen Angaben kann $p$ berechnet werden.
  Berechne dann $\sigma=\sqrt{n\cdot p\cdot (1-p)}$ .
2. Die Wahrscheinlichkeit $P(X \geq 61)$ beträgt etwa $2 %$ .
  Bestimmen Sie unter Verwendung dieses Wertes den zugehörigen Wert für die Wahrscheinlichkeit $P(40 \leq X \leq 60)$ . (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
  Bestimme unter Verwendung dieses Wertes den zugehörigen Wert für die Wahrscheinlichkeit $P(40 \leq X \leq 60)$
  Vorausgesetzt wird, dass die Wahrscheinlichkeitsverteilung von $X$ wegen $p=\dfrac{1}{2}$ symmetrisch um den Erwartungswert liegt.
  Mit dieser Annahme ist also $P(X\leq 39)=P(X\geq 61)$
  Die Wahrscheinlichkeit $P(X \geq 61)$ beträgt etwa $2 %$ , d.h. $P(X\leq 39)$ beträgt somit auch $2 %$ .
  Andererseits ist $P(X\leq 60)=1-P(X \geq 61)=1-0{,}02=0{,}98$ .
  Somit ist dann: ⁣ $P(40 \leq X \leq 60)=P(X \leq 60)-P(X \leq 39)=0{,}98-0{,}02=0{,}96$ .
  Der zugehörige Wert für die Wahrscheinlichkeit $P(40 \leq X \leq 60)$ ist $0,96$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Vorausgesetzt wird, dass die Wahrscheinlichkeitsverteilung von $X$ wegen $p=\dfrac{1}{2}$ symmetrisch um den Erwartungswert liegt.
  Mit dieser Annahme ist also $P(X\leq 39)=P(X\geq 61)$
  Berechne dann $P(40 \leq X \leq 60)=P(X \leq 60)-P(X \leq 39)$ .
6
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 6
Bei einem Gewinnspiel beträgt der Einsatz für die Teilnahme $3$ Euro. Die Auszahlung in Euro wird durch die Zufallsgröße $A$ beschrieben.
Abbildung 5 zeigt die Wahrscheinlichkeitsverteilung von $A$ .
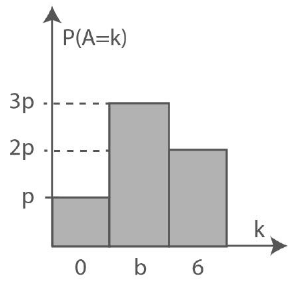
Abbildung 5
1. Zeigen Sie, dass $p$ den Wert $\frac{1}{6}$ hat. (1 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
  Zeige, dass $p$ den Wert $\frac{1}{6}$ hat
  Der Abbildung entnimmt man, dass $p + 3 p + 2 p = 1$ ist $\;\Rightarrow\;6p=1\;\Rightarrow\;p=\dfrac{1}{6}$ .
  Damit ist gezeigt, dass $p$ den Wert $\frac{1}{6}$ hat.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Bei wiederholter Durchführung des Spiels ist zu erwarten, dass sich auf lange Sicht Einsätze und Auszahlungen ausgleichen.
  Berechnen Sie den Wert von $b$ . (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Erwartungswert
  Berechne den Wert von $b$
  Der Einsatz für die Teilnahme beträgt $3$ Euro.
  Wenn sich auf lange Sicht Einsätze und Auszahlungen ausgleichen, muss $E (A) = 3$ sein. Es ist $p=\dfrac{1}{6}$ .
  Dann folgt:
  $E(A)=\dfrac{1}{6}\cdot 0+\dfrac{3}{6}\cdot b+\dfrac{2}{6}\cdot 6=3\;\Rightarrow\;\dfrac{3}{6}\cdot b=1\;\Rightarrow\;b=2$
  Der Wert von $b$ beträgt 2.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Wenn sich auf lange Sicht Einsätze und Auszahlungen ausgleichen, muss $E (A) = 3$ sein. Es ist $p=\dfrac{1}{6}$ .
  Stelle für $E (A)$ eine Gleichung auf und löse sie nach $b$ auf.
3. Beschreiben Sie, wie das Gewinnspiel unter Verwendung eines Behälters sowie roter, grüner und blauer Kugel durchgeführt werden könnte. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
  Beschreibe, wie das Gewinnspiel unter Verwendung eines Behälters sowie roter, grüner und blauer Kugel durchgeführt werden könnte
  Entsprechend der angegebenen Wahrscheinlichkeiten werden in den Behälter $1$ grüne, $3$ rote und $2$ blaue Kugeln gelegt.
  Dem Behälter wird zufällig eine Kugel entnommen und die Farbe betrachtet.
  Ist die Farbe der Kugel grün, dann erfolgt keine Gewinnauszahlung.
  Ist die Farbe der Kugel rot, dann werden $2 €$ ausgezahlt.
  Ist die Farbe der Kugel blau, dann werden $6 €$ ausgezahlt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Lege entsprechend der Wahrscheinlichkeit eine Anzahl von roten, grünen und blauen Kugeln in den Behälter und ziehe einmal eine Kugel.
  Bestimme die Auszahlung für die gezogene Farbe der Kugel.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

A2

Aufgabe 1

Zeige, dass f′(x)=2x⋅(2x2−k)f'(x)=2x\cdot(2x^2-k)f′(x)=2x⋅(2x2−k) eine Gleichung der ersten Ableitungsfunktion von fff ist

Hast du eine Frage oder Feedback?

Ermittele den Wert von kkk

Hast du eine Frage oder Feedback?

Aufgabe 2

Interpretiere die Aussage F(5)−F(1)=0F(5)-F(1)=0F(5)−F(1)=0 in Bezug auf den Graphen von fff

Hast du eine Frage oder Feedback?

Berechne ∫01f(x) dx\displaystyle\int_0^1 f(x)\;\mathrm{d}x∫01​f(x)dx

Hast du eine Frage oder Feedback?

Aufgabe 3

Ermittle die beiden Extremstellen von fff.

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Aufgabe 4

Ermittle diesen Wert von aaa

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Aufgabe 5

Berechne die Standardabweichung von XXX

Hast du eine Frage oder Feedback?

Bestimme unter Verwendung dieses Wertes den zugehörigen Wert für die Wahrscheinlichkeit P(40≤X≤60)P(40 \leq X \leq 60)P(40≤X≤60)

Hast du eine Frage oder Feedback?

Aufgabe 6

Zeige, dass ppp den Wert 16\frac{1}{6}61​ hat

Hast du eine Frage oder Feedback?

Berechne den Wert von bbb

Hast du eine Frage oder Feedback?

Beschreibe, wie das Gewinnspiel unter Verwendung eines Behälters sowie roter, grüner und blauer Kugel durchgeführt werden könnte

Hast du eine Frage oder Feedback?

Zeige, dass $f'(x)=2x\cdot(2x^2-k)$ eine Gleichung der ersten Ableitungsfunktion von $f$ ist

Ermittele den Wert von $k$

Interpretiere die Aussage $F (5) - F (1) = 0$ in Bezug auf den Graphen von $f$

Berechne $\displaystyle\int_0^1 f(x)\;\mathrm{d}x$

Ermittle die beiden Extremstellen von $f$ .

Ermittle diesen Wert von $a$

Berechne die Standardabweichung von $X$

Bestimme unter Verwendung dieses Wertes den zugehörigen Wert für die Wahrscheinlichkeit $P(40 \leq X \leq 60)$

Zeige, dass $p$ den Wert $\frac{1}{6}$ hat

Berechne den Wert von $b$