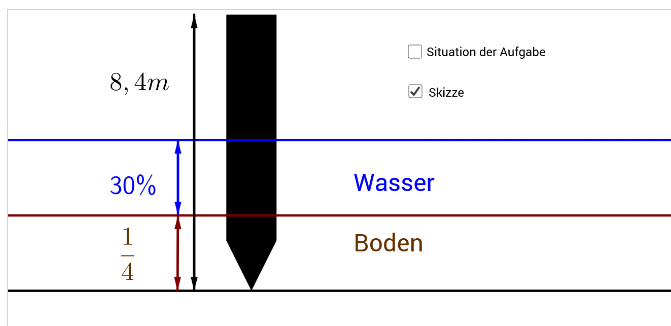
Ein 8,4m langer Pfahl steckt zu im Boden und zu 30% im Wasser. Fertige eine Skizze mit den gegebenen Daten an und berechne wie viele Meter des Pfahls aus dem Wasser herausragen.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?