Wenn man den Abstand eines Punktes zu einer Geraden bestimmen möchte, muss man beachten, dass mit Abstand immer der kürzeste Abstand gemeint ist.
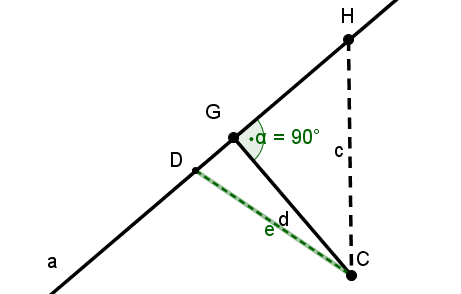
Gesucht ist der Abstand von Punkt zur Geraden . Betrachtet man die Zeichnung rechts, sieht man, dass die Strecke zwischen und , auch genannt, dieser gesuchte kürzeste Abstand ist. (Diesen erkennt man an dem rechten Winkel zwischen der Geraden und der Strecke .) Die Strecken und sind zwar auch Abstände, aber länger als und somit nicht der gesuchte Abstand.
Die Gerade wird auch Lot genannt.
Mit Geodreieck messen
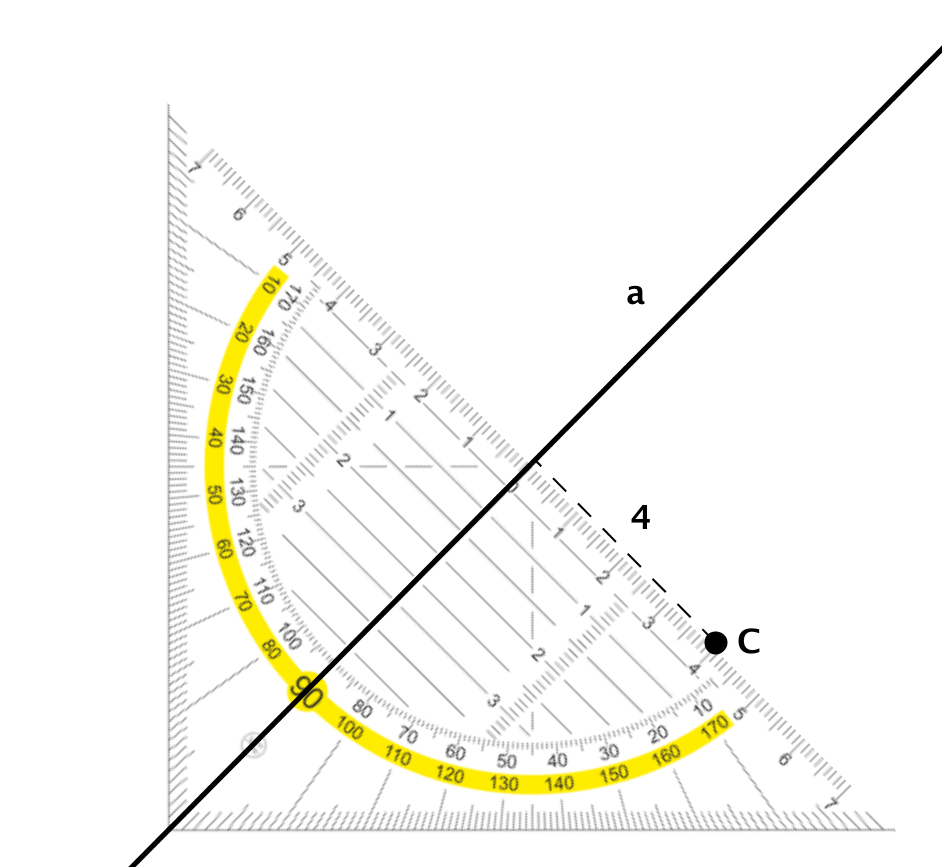
Man legt das Geodreieck so an die Gerade an, dass die Mittellinie des Geodreiecks, die durch die Null verläuft, genau auf der Geraden liegt.
Man verschiebt nun das Geodreieck entlang der Geraden, sodass der Punkt auf der Skala des Geodreiecks liegt.
Nun lässt sich der Abstand des Punktes zu der Geraden auf dem Geodreieck ablesen.
Im Beispiel rechts entspricht der Abstand 4 cm.
Übungsaufgabe
Zeichne zu den gegebenen Punkten , und die Gerade und den Punkt in ein Koordinatensystem ein und miss den Abstand mit einem Geodreieck.
Laden
Konstruktion der kürzesten Verbindung des Punkts mit der Geraden
Gegeben: Gerade und Punkt
Man bestimmt nun den Abstand wie folgt:
Man zeichnet einen Kreis mit Mittelpunkt , so dass der Kreis die Gerade in zwei Punkten und schneidet.
Dann konstruiert man eine Mittelsenkrechte zu den Punkten und .
Der Schnittpunkt der Geraden und der Mittelsenkrechte wird mit bezeichnet.
Jetzt kann der Abstand zwischen und abgemessen werden.
Im folgenden Applet wird die Konstruktion noch einmal schrittweise gezeigt. Ziehe dazu einfach den Regler nach rechts.
Übungsaufgabe
Bestimme zu den gegebenen Punkten , und den Abstand der Gerade zu dem Punkt .
Laden
Video zum Thema Abstand eines Punktes zu einer Geraden
Laden
Übungsaufgaben
Laden
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Gemischte Aufgaben zu Geraden, Strecken oder Halbgeraden
