Sachaufgaben zum Koordinatensystem

1
In einer Landkarte mit Koordinatensystem, wobei ein Kästchen ( $5\ mm$ ) einem Kilometer entspricht, sind folgende Ortschaften eingetragen:
Achkirchen: $A(4|3)$
Bergheim: $B(24|18)$
Dachshausen: $D(21|3)$
Eberfing: $E(3|15)$
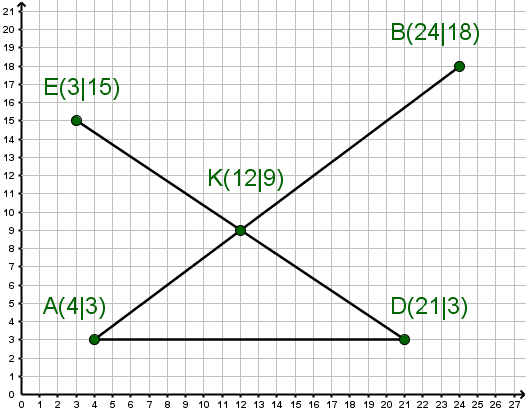
Drei gerade Straßen verbinden Achkirchen mit Bergheim, Dachshausen mit Eberfing und Achkirchen mit Dachshausen.
1. Zeichne die Orte und Straßen in ein geeignetes Koordinatensystem. Welche Koordinaten hat die Kreuzung $K$ der beiden Straßen?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Punkte und Strecken zeichnen
  Die Punkte und Strecken zeichnest du einfach in ein Koordinatensystem ein:
  Dann liest du die Koordinaten der Kreuzung ab: $K(12|9)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Die Straße zwischen Achkirchen und Dachshausen sei nun ein Feldweg. Ein Fußgänger legt auf einer Straße $7\ km$ in einer Stunde zurück, auf dem Feldweg nur $5\ km$ pro Stunde. Wie lange braucht der Fußgänger von Achkirchen nach Dachshausen, wenn er auf der Straße über die Kreuzung $K$ geht? Wie lange braucht er, wenn er stattdessen den Feldweg benutzt? Verwende ein Lineal zum Ausmessen der benötigten Straßenlängen und runde dabei auf ganze Kilometer.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Dreisatz
  Zeit ausrechnen
  Als Erstes misst du mit dem Lineal aus, wie weit der Fußgänger laufen muss, wenn er die Straße benutzt. Von Achkirchen bis zur Kreuzung sind das $10\ km$ , von der Kreuzung bis nach Dachshausen etwa $11\ km$ . Also insgesamt 21 km. Der Fußgänger braucht für 7 km eine Stunde; mit dem Dreisatz kannst du daraus berechnen: Für 21 km braucht er 3 Stunden.
  Nun misst du, wie weit der Fußgänger läuft, wenn er den Feldweg benutzt: 17 km. Da der Fußgänger auf dem Feldweg nur $5\ km$ pro Stunde schafft, ergibt das mit dem Dreisatz: Er braucht für $1\ km$ $12\ \min$ , also für $17\ km$ $204\ \min$ oder $3\ h$ und $24\ \min$ .
  Er braucht also $24\ \min$ länger, wenn er den Feldweg benutzt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2
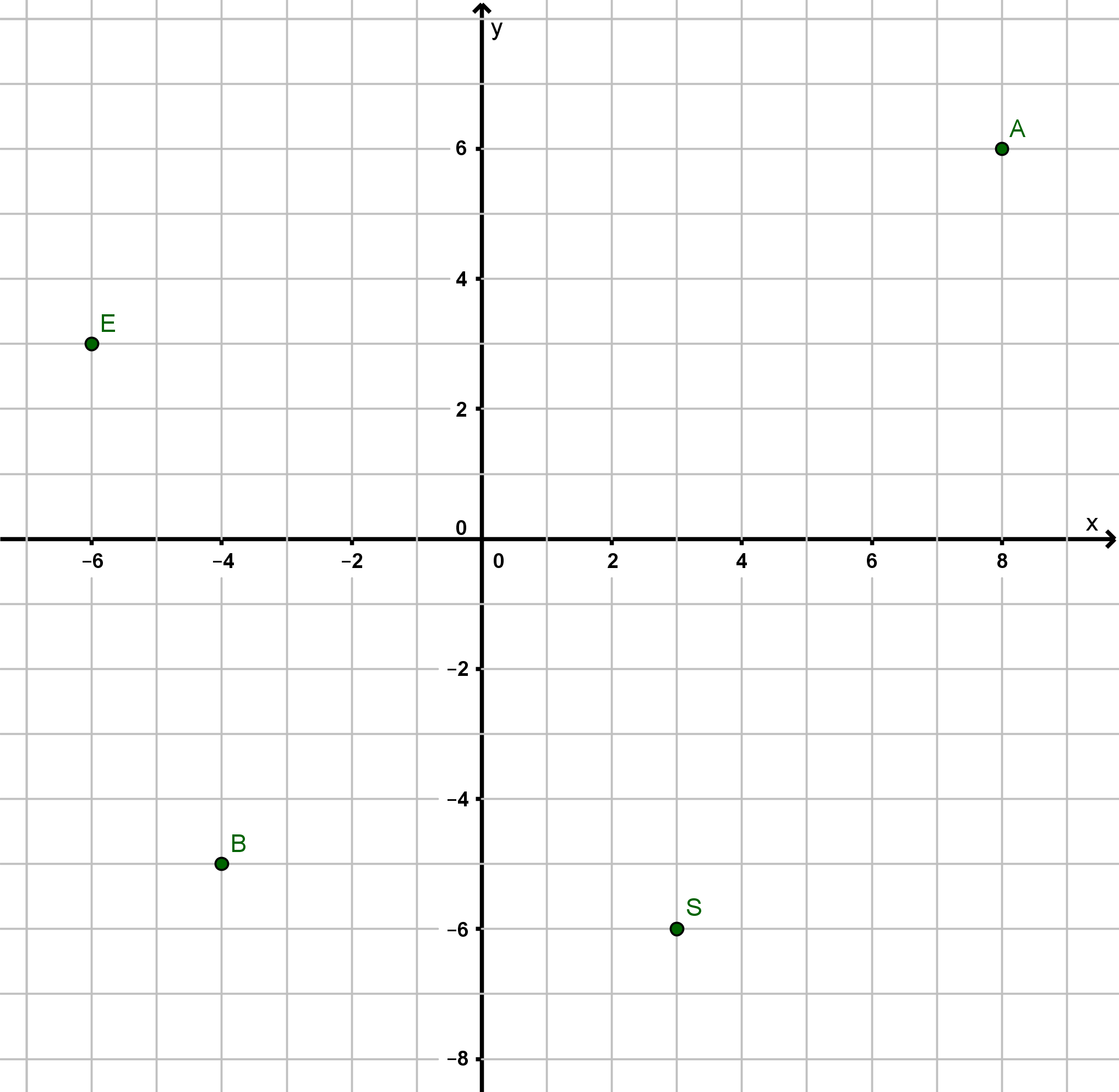
Auf eine Landkarte, in der $5\ mm$ einem Kilometer entsprechen, ist ein Koordinatensystem aufgedruckt. Albert wohnt bei $A(8|6)$ , Eva bei $E(-6|3)$ und Bert bei $B(-4|-5)$ , die Schule ist am Ort $S(3|-6)$ (alle Zahlenwerte entsprechen Kilometern).
1. Welchen Maßstab hat die Karte?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Maßstab berechnen
  $5\ mm$ auf der Landkarte entsprechen einem Kilometer in der Wirklichkeit.
  Um besser rechnen zu können, wandelst du die Längen in eine gemeinsame Einheit um: $1\ km=1000\ m=1000000\ mm$ .
  Teile beide Längen durch die kleinere, in diesem Fall $5\ mm$ : Der Maßstab $5 : 1 000 000$ entspricht also $1 : 200 000$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Zeichne die Punkte $A, E, B$ und $S$ in ein Koordinatensystem (gleicher Maßstab wie die Landkarte).
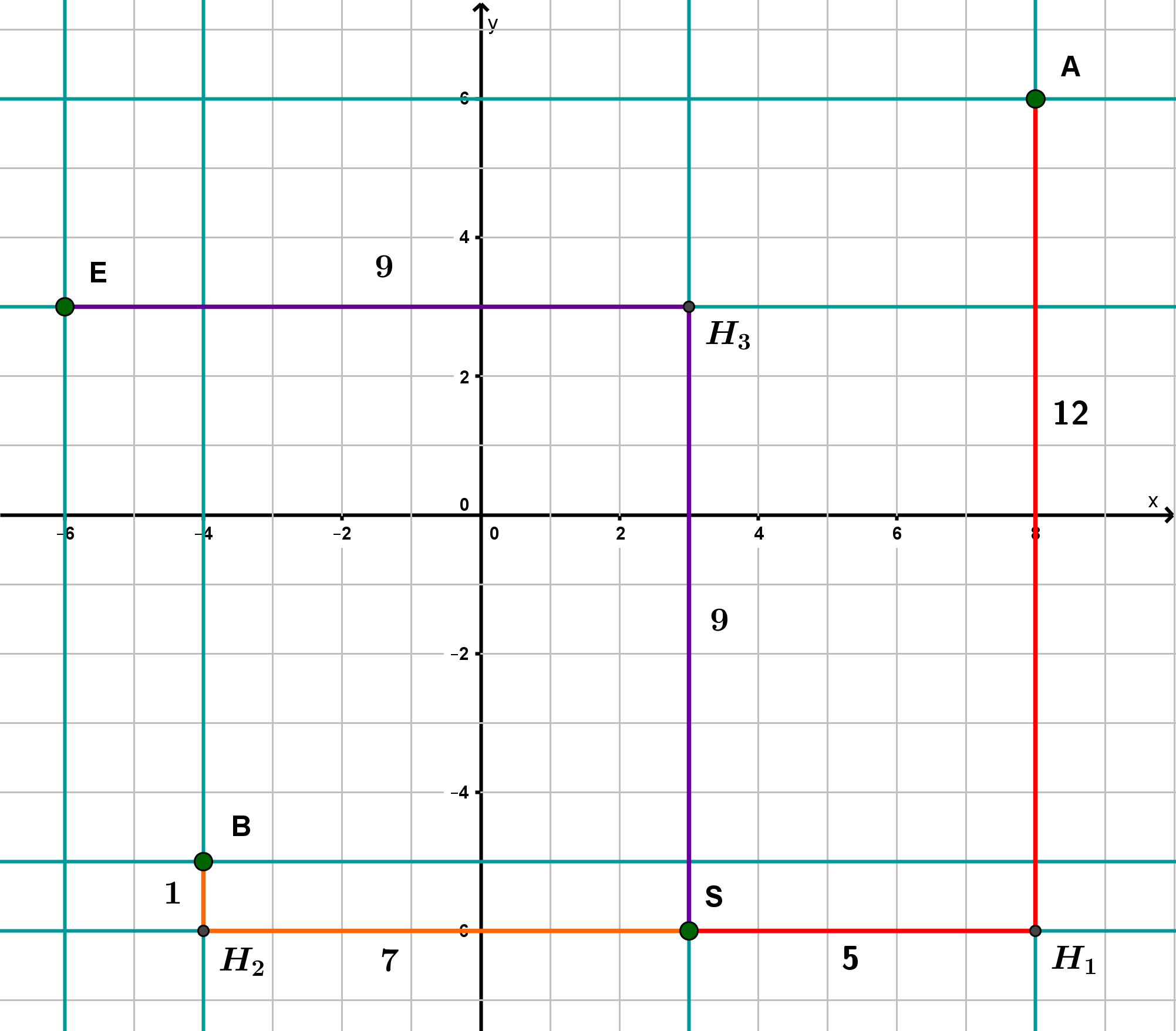
  Durch jeden Wohnort und durch den Ort der Schule gehen zwei Straßen, die parallel zu den Koordinatenachsen verlaufen (waagrecht und senkrecht). Zeichne diese Straßen in das Koordinatensystem ein.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Punkte in ein Koordinatensystem einzeichnen
  Im Folgenden zeichnest du die Straßen in das Koordinatensystem ein.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Ermittle die kürzesten Weglängen von den Wohnorten zur Schule (auf den Straßen).
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Weglängen berechnen
  $A(8∣6),B(-4|-5),E(-6|3),S(3|-6)$
  Hilfspunkte:
  $H_1(8|-6),H_2(-4|-6),H_3(3|3)$
  Du verwendest diese Formeln:
  $d_y=y_{oben}-y_{unten}$
  $d_x=x_{rechts}-x_{links}$
  $d_{gesamt}=d_y+d_x$
  Der Schulweg von Albert
  $d_y=6-(-6)=12$
  $d_x=8-3=5$
  $d_{Albert}=5+12=17$
  Für den Schulweg von Albert benutzt du den Hilfspunkt $H_1$ . Die Strecke ist erst parallel zur y-Achse und dann parallel zur x-Achse.
  Der Schulweg von Bert
  $d_y=-5-(-6)=1$
  $d_x=3-(-4)=7$
  $d_{Bert}=1+7=8$
  Für den Schulweg von Bert benutzt du den Hilfspunkt $H_2$ . Die Strecke ist erst parallel zur y-Achse und dann parallel zur x-Achse.
  Der Schulweg von Eva
  $d_x=3-(-6)=9$
  $d_y=3-(-6)=9$
  $d_{Eva}=9+9=18$
  Für den Schulweg von Eva benutzt du den Hilfspunkt $H_3$ . Die Strecke ist erst parallel zur x-Achse und dann parallel zur y-Achse.
  Eine Längeneinheit auf der Karte entspricht einem Kilometer in Wirklichkeit, d.h. Albert hat einen Schulweg von $17\ km$ , Bert einen von $8\ km$ und Eva einen von $18\ km$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. Auf wie vielen verschiedenen kürzesten Wegen kann Eva in die Schule gehen?
  
  4. Anzahl der Schulwege zählen
  Es gibt $6$ verschiedene Wege, die Eva gehen kann. Ziehe am Schieberegler, um die Wege zu sehen.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
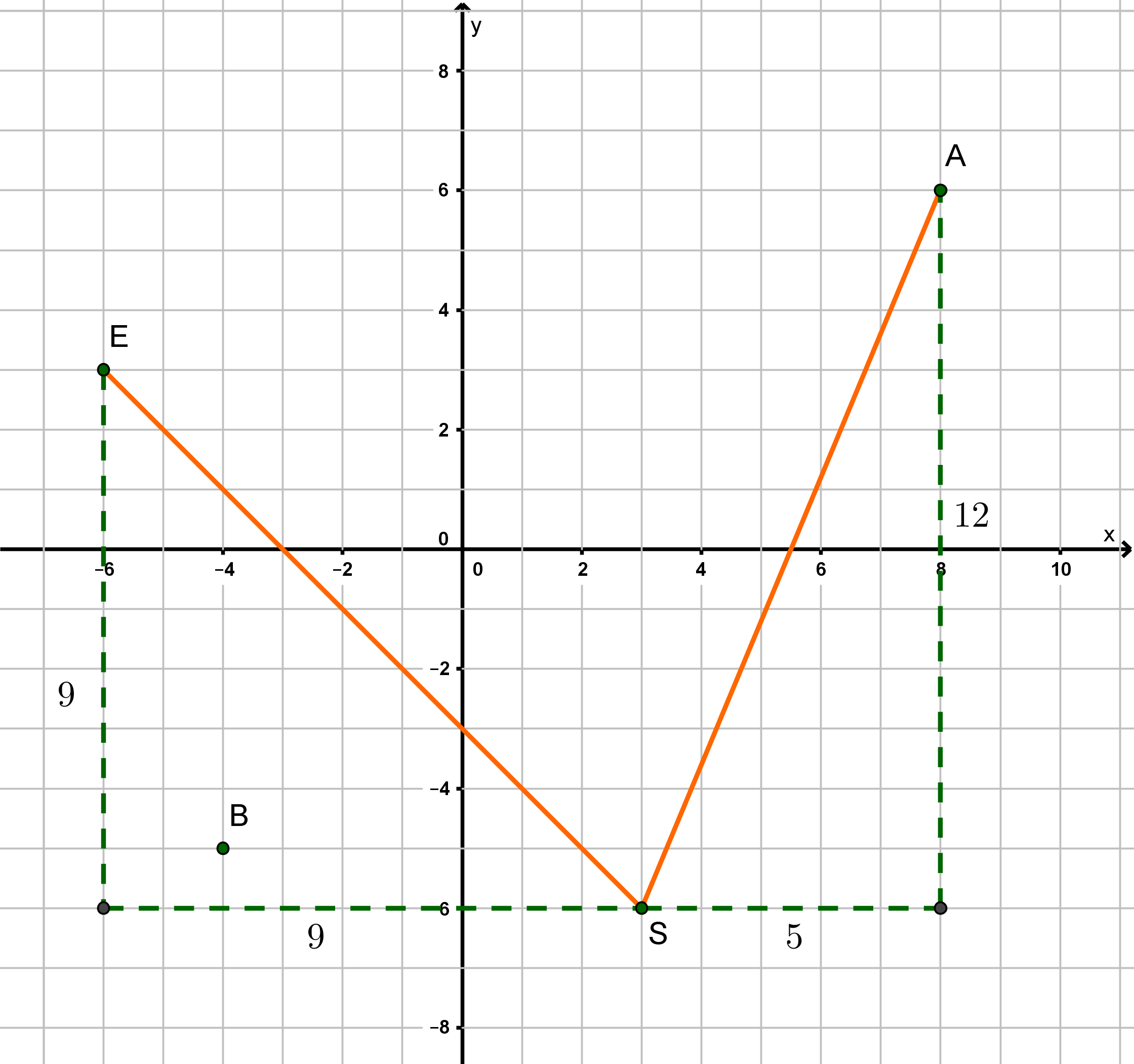
5. Wie weit ist es querfeldein (geradlinig) von Alberts Wohnort zur Schule? Wie lang wäre eine gerade Straße von Evas Wohnort zur Schule?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Direkte Weglänge berechnen
  Berechnet werden müssen die direkten Weglängen $[AS]$ und $[ES]$ .
  Die Straßen bilden mit den direkten Wegen zwei rechtwinklige Dreiecke. Du kannst also den Satz des Pythagoras verwenden.
  Du berechnest jeweils die Hypotenuse dieser Dreiecke.
  $c=\sqrt{a^2+b^2}$
  $[AS]=\sqrt{12^2+5^2}=13km$
  $[ES]=\sqrt{9^2+9^2}\approx12{,}7km$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉