Geometrie, Teil A, Aufgabengruppe 1

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
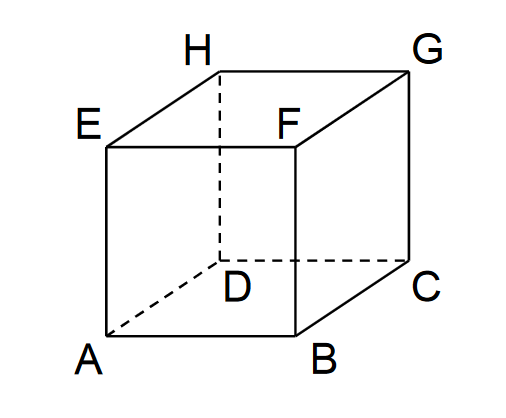
Betrachtet wird der abgebildete Würfel $A B C D E F G H$ . Die Eckpunkte $D$ , $E$ , $F$ und $H$ dieses Würfels besitzen in einem kartesischen Koordinatensystem die folgenden Koordinaten: $D (0 ∣ 0 ∣ - 2)$ , $E (2 ∣ 0 ∣ 0)$ , $F (2 ∣ 2 ∣ 0)$ und $H (0 ∣ 0 ∣ 0)$ .
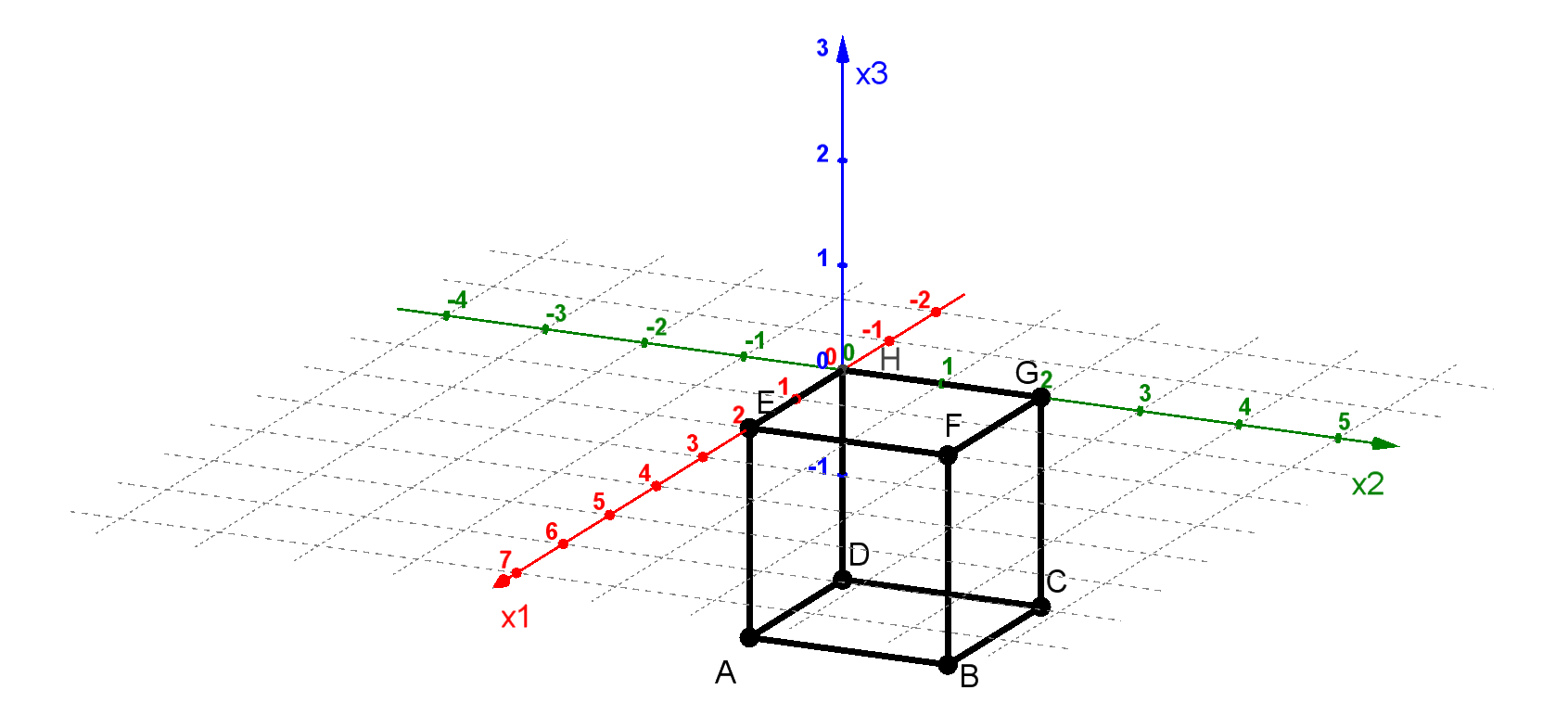
1. Zeichnen Sie in die Abbildung die Koordinatenachsen ein und bezeichnen Sie diese. Geben Sie den Koordinaten des Punkts $A$ an. (2 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Koordinatensystem
  Einzeichnen des Koordinatensystems
  Wie du bereits weißt, ist ein Würfel dreidimensional. Somit musst du ein dreidimensionales Koordinatensystem verwenden.
  Der Ursprung eines solchen Koordinatensystems hat die Koordinaten $(0 ∣ 0 ∣ 0)$ . Der angegebene Punkt $H$ hat genau diese Koordinaten. Das bedeutet, dass das Koordinatensystem durch diesen Punkt geht.
  Du kannst mithilfe von den angegebenen Punkten $D$ , $E$ und $F$ leicht überprüfen, dass diese ins Koordinatensystem passen.
  Da die eingezeichneten Punkte $3$ Koordinatenbestandteile haben, solltest du die Koordinatenachsen als $x_{1}$ , $x_{2}$ und $x_{3}$ definieren.
  Koordinaten des Punktes $A$
  Ein Würfel hat gleich lange Seiten, die durch gleich lange Vektoren repräsentiert werden.
  $|\overrightarrow{HE}|=\left|\begin{pmatrix}2\\0\\0\end{pmatrix} - \begin{pmatrix}0\\0\\0\end{pmatrix}\right| = \left| \begin{pmatrix}2\\0\\0\end{pmatrix} \right| = \sqrt{2^2+0^2+0^2} = 2$
  Entsprechend der Zeichnung liegt der Punkt $A$ direkt unter dem Punkt $E$ . Die Seitenlänge dieser Strecke $[E A]$ ist also auch $2$ . Nun überlegt man sich folgendes:
  $A$ liegt direkt unter $E$ . Die $x_{1}$ -Koordinate muss also gleich bleiben.
  $x_{1} : 2$
  Dementsprechend ist $A$ auch in der $x_{2}$ -Achse nicht verschoben.
  $x_{2} : 0$
  $A$ ist aufgrund der Seitenlänge um $2$ Längeneinheiten (LE) nach unten verschoben.
  $x_{3} :$ nach unten um $2$ LE $\rightarrow$ $- 2$
  Der Punkt $A$ hat also die Koordinaten $(2 ∣ 0 ∣ - 2)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Der Punkt $P$ liegt auf der Kante $[F B]$ des Würfels und hat vom Punkt $H$ den Abstand $3$ . Berechnen Sie die Koordinaten des Punkts $P$ . (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Koordinatensystem
  Das erste, was dir auffallen sollte ist, dass der Abstand: $\overline{HP} = 3$
  $|\overrightarrow{HP}| = \left| \begin{pmatrix}p_1\\p_2\\p_3\end{pmatrix} - \begin{pmatrix}0\\0\\0\end{pmatrix} \right| = \left| \begin{pmatrix}p_1\\p_2\\p_3\end{pmatrix} \right| = \sqrt{p_1^2 + p_2^2 + p_3^2} = 3$
  Die zweite Information, die dich ab diesem Schritt weiterbringt, ist, dass $P$ auf der Kante $[F B]$ liegt. Deshalb haben $F$ und $B$ die gleiche $x_{1}$ - und $x_{2}$ -Koordinate.
  $p_{1} = 2$
  $p_{2} = 2$
  Mit dieser Erkenntnis kannst du auch die verbliebene dritte Koordinate $p_{3}$ des Punktes $P$ finden.
  $|\overrightarrow{HP}| = \sqrt{p_1^2+p_2^2+p_3^2} = \sqrt{2^2+2^2+p_3^2} = \sqrt{8+p_3^2} = 3$
  Rechne die mögliche(n) Lösung(en) für $p_{3}$ aus.
  $\def\arraystretch{1.25} \begin{array}{rlr} \sqrt{8+{p_3}^2} &= &3 &|{\ldots}^2\\8+p_3^2 &=& 9 &| - 8\\p_3^2 &=& 1 &\sqrt{\ldots}\\p_3&=&\pm 1 \end{array}$
  Der Punkt muss auf der Strecke zwischen $B$ und $F$ liegen, also muss auch seine $x_{3}$ -Koordinate zwischen der von $B$ und der von $F$ liegen. Damit muss die $x_{3}$ -Koordinate zwischen $- 2$ und $0$ liegen.
  Die dritte Koordinate für $P$ ist entweder $- 1$ oder $1$ . Da allerdings $1$ nicht in der Menge $[- 2, 0]$ liegt, bleibt dir nur noch eine Möglichkeit.
  Die Koordinaten des Punktes $P$ sind also $(2 ∣ 2 ∣ - 1)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Gegeben sind die Punkte $A (- 2 ∣ 1 ∣ 4)$ und $B (- 4 ∣ 0 ∣ 6)$ .

Bestimmen Sie die Koordinaten des Punkts $C$ so, dass gilt: $\overrightarrow{CA} = 2 \cdot \overrightarrow{AB}$ . (2 BE)

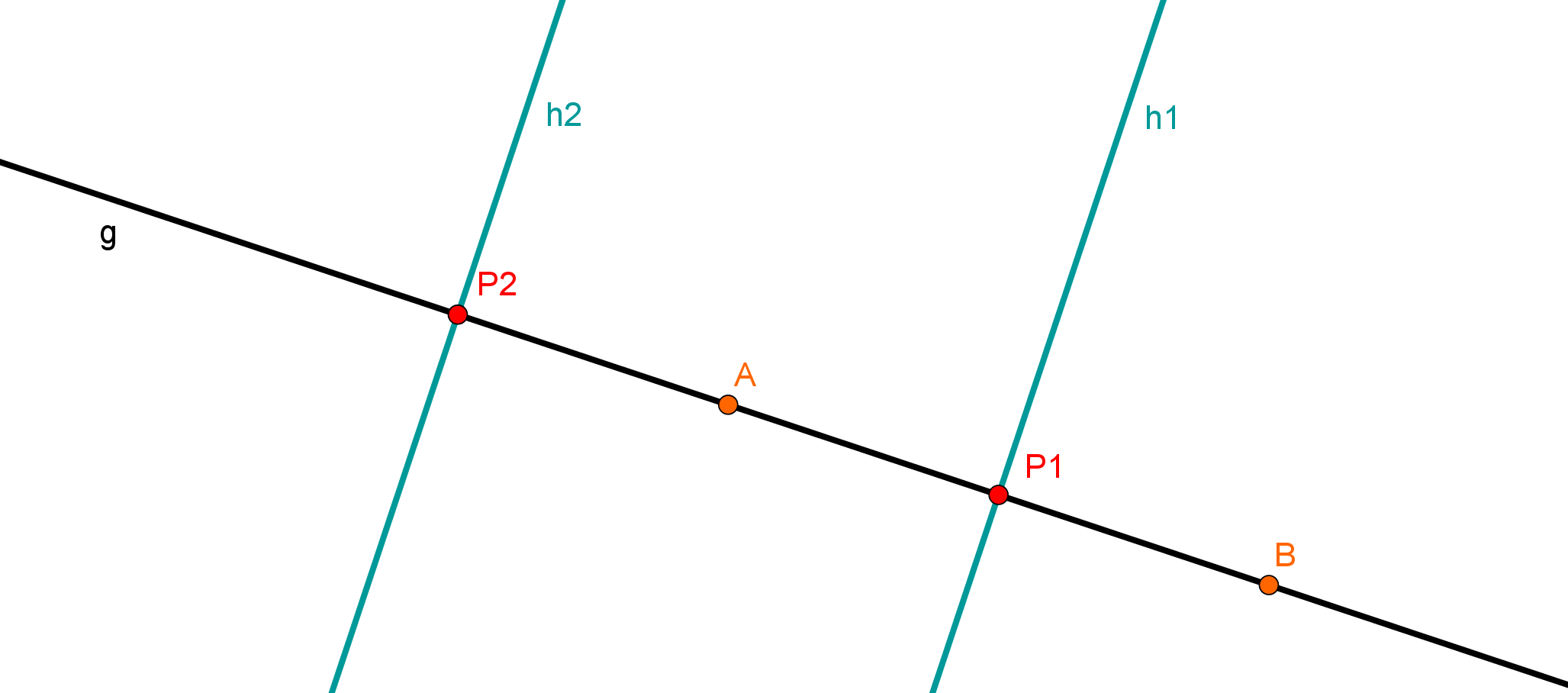
Durch die Punkte $A$ und $B$ verläuft die Gerade $g$ . Betrachtet werden Geraden, für welche die Bedingungen $\mathrm{I}$ und $\mathrm{II}$ gelten:

$\mathrm{I}:$ Jede dieser Geraden schneidet die Gerade $g$ orthogonal. $\mathrm{II}:$ Der Abstand jeder dieser Geraden vom Punkt $A$ beträgt $3$ .

Ermitteln Sie eine Gleichung für eine dieser Geraden. (3 BE)

Die allgemeine Geradengleichung in der analytischen Geometrie lässt sich schreiben als $h: \overrightarrow{x} = \overrightarrow{P} + \lambda \overrightarrow{u}$

Bedingung $\mathrm{I}$ : Orthogonalität

Zwei Vektoren stehen orthogonal zueinander, wenn sie senkrecht aufeinander stehen. Dies ist der Fall, falls ihr Skalarprodukt Null ergibt.

Bei Geraden überprüfst du diese Bedingung, indem du das Skalarprodukt ihrer Richtungsvektoren bildest. Der Richtungsvektor von $g$ ist der Vektor

\displaystyle \overrightarrow{AB}=\begin{pmatrix}-2\\-1\\2\end{pmatrix}

(siehe a)).

$\def\arraystretch{1.25} \begin{array}{rrl}\overrightarrow{AB} \circ \overrightarrow u &= &0 \\\begin{pmatrix}-2\\-1\\2\end{pmatrix} \circ \begin{pmatrix}u_1\\u_2\\u_3\end{pmatrix} &= &0 \\-2u_1 + (-u_2) + 2u_3 &= &0\end{array}$

Allerdings bekommst du eine Gleichung mit drei Unbekannten. In solch einem Fall darfst du zwei Unbekannte frei auswählen.

Du kannst hierfür z. B. $u_{1} = t$ und $u_{3} = t$ für $t \in \mathbb{R}$ allgemein festlegen. Dann gilt

$\displaystyle -2u_1-u_2+2u_3$	$=$	$\displaystyle 0$
$\displaystyle -2t-u_2+2t$	$=$	$\displaystyle 0$
$\displaystyle -u_2$	$=$	$\displaystyle 0$
$\displaystyle u_2$	$=$	$\displaystyle 0$

Der Richtungsvektor der neuen Gerade $h$ lautet also

$\overrightarrow{u} = \begin{pmatrix}t\\0\\t\end{pmatrix} = t \cdot \begin{pmatrix}1\\0\\1\end{pmatrix}$

Bedingung $\mathrm{II}$ : Abstand

Es fehlt nur noch der Stützpunkt $P$ der Gerade $h$ . Dieser soll zum Stützpunkt $A$ der Gerade $g$ den Abstand $3$ haben.

Wie du auch auf dem Bild unten erkennen kannst, gibt es zwei Möglichkeiten, eine passende Gerade $h$ zu finden.

Der Stützpunkt $P_{1}$ bzw. $P_{2}$ haben den Abstand $3$ zu dem Punkt $A$ .

Vielleicht fällt dir direkt auf, dass der Abstand von Punkt $A$ zu Punkt $B$ die Länge hat:

$|\overrightarrow{AB}|=|\begin{pmatrix}-2\\-1\\2\end{pmatrix}|\\=\sqrt{(-2)^2+(-1)^2+2^2}\\=\sqrt{9}=3$

Damit eignet sich der Punkt $B$ als Aufpunkt und eine der möglichen Geraden ist:

\displaystyle \overrightarrow{AB}=\begin{pmatrix}-2\\-1\\2\end{pmatrix}

Dann bist du an dieser Stelle fertig. Wenn dir das nicht aufgefallen ist, kannst du auch folgendem, allgemeinem Schema folgen:

Normiere den Vektor $\overrightarrow{AB}$ , bringe ihn also zuerst auf die Länge $1$ .

$\displaystyle \frac{\overrightarrow{AB}}{\|\overrightarrow{AB}\|}$	$=$	$\displaystyle \frac{\begin{pmatrix}-2\\-1\\2\end{pmatrix}}{\sqrt{(-2)^2+(-1)^2+2^2}} \\$
	$=$	$\displaystyle \frac{1}{3} \cdot \begin{pmatrix}-2\\-1\\2\end{pmatrix}$

Multipliziere diese Normierung mit $3$ , um den richtigen Abstand zu bekommen.

$\displaystyle 3 \cdot \frac{\overrightarrow{AB}}{\|\overrightarrow{AB}\|}$	$=$	$\displaystyle 3 \cdot \frac{1}{3} \cdot \begin{pmatrix}-2\\-1\\2\end{pmatrix} \\$
	$=$	$\displaystyle \begin{pmatrix}-2\\-1\\2\end{pmatrix}$

Nun kannst du den Stützpunkt $P_ {1{,}2}$ der Geraden $h_{1{,}2}$ berechnen, indem du ihn zum Stützpunkt $A$ addierst bzw. von $A$ subtrahierst.

\displaystyle \overrightarrow{P_{1{,}2}}

=

\displaystyle \overrightarrow{A} \; \pm \; 3 \cdot \frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}

$\displaystyle \\\overrightarrow{P_1}$	$=$	$\displaystyle \overrightarrow{A} + 3 \cdot \frac{\overrightarrow{AB}}{\|\overrightarrow{AB}\|}$
	$=$	$\displaystyle \begin{pmatrix}-2\\1\\4\end{pmatrix} + \begin{pmatrix}-2\\-1\\2\end{pmatrix}$
	$=$	$\displaystyle \begin{pmatrix}-4\\0\\6\end{pmatrix}$

$\displaystyle \\\overrightarrow{P_2}$	$=$	$\displaystyle \overrightarrow A - 3 \cdot \frac{\overrightarrow{AB}}{\|\overrightarrow{AB}\|}$
	$=$	$\displaystyle \begin{pmatrix}-2\\1\\4\end{pmatrix} - \begin{pmatrix}-2\\-1\\2\end{pmatrix}$
	$=$	$\displaystyle \begin{pmatrix}0\\2\\2\end{pmatrix}$

Die gesuchten Geraden sind also

$h_1: \overrightarrow{x} = \begin{pmatrix}-4\\0\\6\end{pmatrix} + t \cdot \begin{pmatrix}1\\0\\1\end{pmatrix}$
$h_2: \overrightarrow{x} = \begin{pmatrix}0\\2\\2\end{pmatrix} + t \cdot \begin{pmatrix}1\\0\\1\end{pmatrix}$

Du musst für eine korrekte Lösung der Aufgabe allerdings nur eine von beiden Gleichungen angeben.

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle \overrightarrow{CA}$	$=$	$\displaystyle 2\cdot\overrightarrow{AB}$
$\displaystyle \begin{pmatrix}-2\\1\\4\end{pmatrix}-\begin{pmatrix}c_1\\c_2\\c_3\end{pmatrix}$	$=$	$\displaystyle 2\cdot\left(\left(\begin{pmatrix}-4\\0\\6\end{pmatrix}-\begin{pmatrix}-2\\1\\4\end{pmatrix}\right)\right)$
$\displaystyle \begin{pmatrix}-2\\1\\4\end{pmatrix}-\begin{pmatrix}c_1\\c_2\\c_3\end{pmatrix}$	$=$	$\displaystyle 2\cdot \begin{pmatrix}-2\\-1\\2\end{pmatrix}$
$\displaystyle \begin{pmatrix}-2\\1\\4\end{pmatrix}-\begin{pmatrix}c_1\\c_2\\c_3\end{pmatrix}$	$=$	$\displaystyle \begin{pmatrix}-4\\-2\\4\end{pmatrix}$
$\displaystyle -\begin{pmatrix}c_1\\c_2\\c_3\end{pmatrix}$	$=$	$\displaystyle \begin{pmatrix}-4\\-2\\4\end{pmatrix}-\begin{pmatrix}-2\\1\\4\end{pmatrix}$
$\displaystyle -\begin{pmatrix}c_1\\c_2\\c_3\end{pmatrix}$	$=$	$\displaystyle \begin{pmatrix}-2\\-3\\0\end{pmatrix}$
$\displaystyle \begin{pmatrix}c_1\\c_2\\c_3\end{pmatrix}$	$=$	$\displaystyle \begin{pmatrix}2\\3\\0\end{pmatrix}$

Geometrie, Teil A, Aufgabengruppe 1

Einzeichnen des Koordinatensystems

Koordinaten des Punktes AAA

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Bedingung I\mathrm{I}I: Orthogonalität

Bedingung II\mathrm{II}II: Abstand

Hast du eine Frage oder Feedback?

Koordinaten des Punktes $A$

Bedingung $\mathrm{I}$ : Orthogonalität

Bedingung $\mathrm{II}$ : Abstand