Lösung zur Teilaufgabe a)

Ermittlung von $B$ und $D$

Die Grundfläche der Pyramide ist ein Quadrat mit der Ecke $A$ im Ursprung und der Ecke $C$ bei $(5|5|0)$. Da $B$ auf der $x_1$-Achse liegt, sind die $x_2$-Koordinate und die $x_3$-Koordinate Null. Die $x_1$-Koordinate muss $5$ sein, damit die Grundfläche quadratisch ist. Also hat $B$ die Koordinaten $(5|0|0)$. Zur Ermittlung des Punkts $D$ kannst du ähnlich vorgehen und erhältst die Koordinaten $(0|5|0)$.

Zeichnen der Pyramide

Trage jetzt die Punkte $A$, $B$, $C$, $D$ und $S$ in ein dreidimensionales Koordinatensystem ein und verbinde sie zur Pyramide $ABCDS$.

Lösung zur Teilaufgabe b)

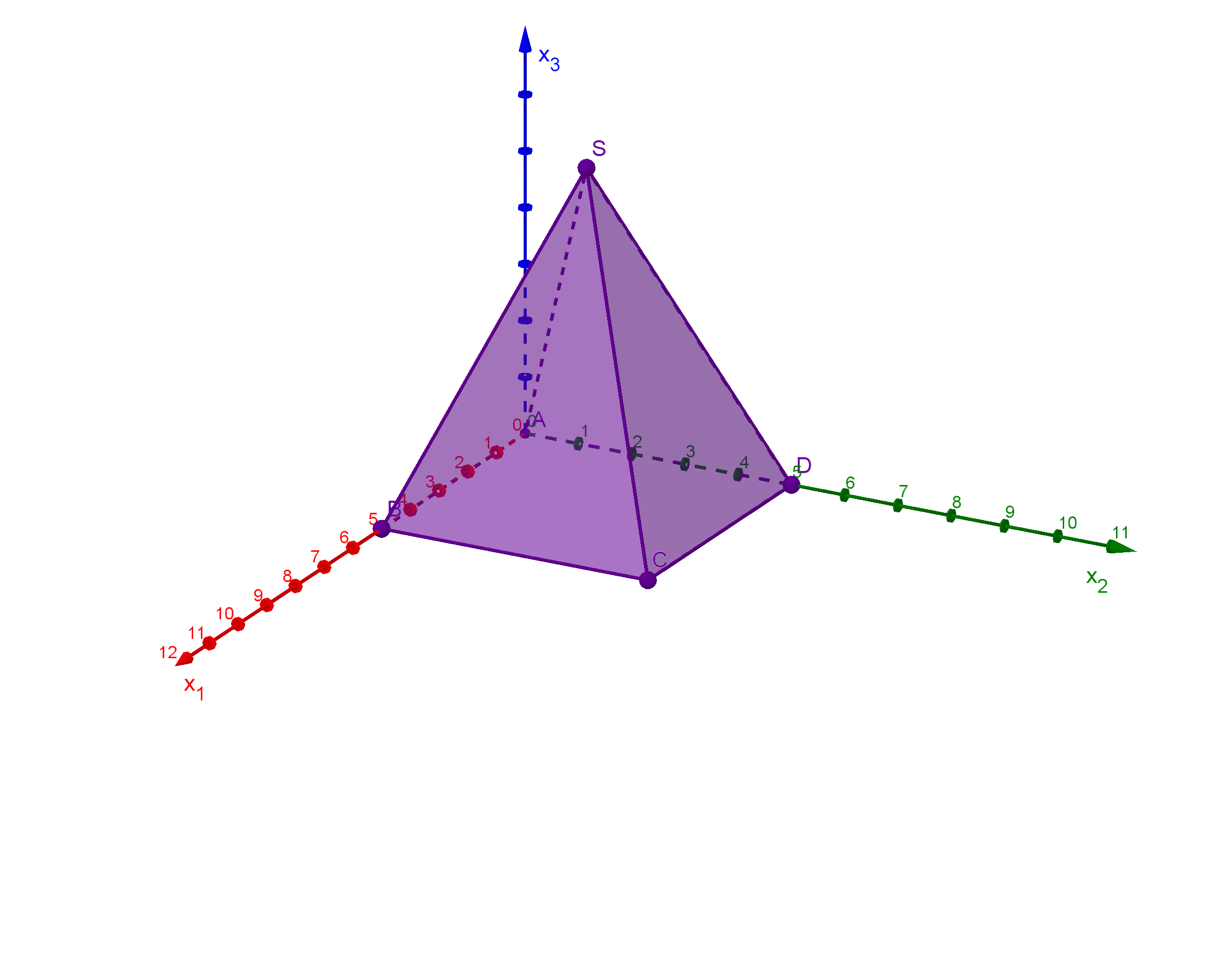
Du kannst die Ebene durch die drei Punkte $A$, $D$ und $S$ aufstellen. Berechne zunächst den Normalenvektor der Ebene $F$.

Berechnung des Normalenvektors

$\overrightarrow{AD}\times\overrightarrow{AS}=\begin{pmatrix}0\\5\\0\end{pmatrix}\times\begin{pmatrix}2{,}5\\2{,}5\\6\end{pmatrix}=\begin{pmatrix}30\\0\\-12{,}5\end{pmatrix}$

Durch Kürzen erhältst du den Normalenvektor $\begin{pmatrix}12\\0\\-5\end{pmatrix}$.

Bestimmung der Ebenengleichung

Diesen kannst du in die allgemeine Ebenengleichung in Normalform einsetzen. $A$ kannst du als Aufpunkt benutzen. Durch Ausmultiplizieren erhältst du die gewünschte Koordinatenform.

$\begin{pmatrix}12\\0\\5\end{pmatrix}\circ\begin{pmatrix}x_1-0\\x_2-0\\x_3-0\end{pmatrix}=0$

$12x_1-5x_3=0$

Lösung zur Teilaufgabe c)

Der Winkel zwischen zwei Ebenen entspricht dem Winkel zwischen den beiden Normalenvektoren der Ebenen.

Ermittlung der Normalenvektoren

Den Normalenvektor der Ebene $E$ kannst du aus der Ebenengleichung ablesen, er ist $\begin{pmatrix}0\\12\\5\end{pmatrix}$. Der Normalenvektor der Ebene $F$ ist $\begin{pmatrix}12\\0\\-5\end{pmatrix}$ (in Teilaufgabe b) berechnet).

Berechnung des Winkels

Benutze nun die Formel zur Berechnung des Winkels zwischen zwei Vektoren.

Lösung zur Teilaufgabe d)

Vorüberlegungen

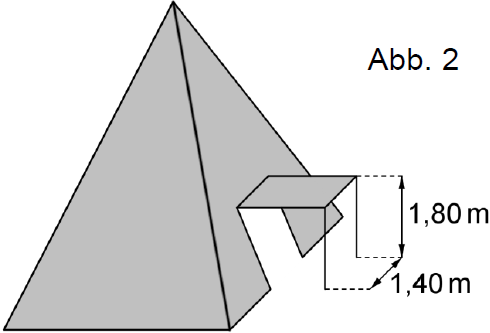
Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Realität, die Lichtquelle (hier genannt $L$) soll also von allen Zeltwänden eine halbe Längeneinheit entfernt sein. Damit die Lichtquelle von allen Wänden den gleichen Abstand hat, muss sie in der Mitte des Zelts hängen; sie hat also die Koordinaten $L(2{,}5|2{,}5|x)$. Wir kennen die Ebenengleichungen für zwei der Zeltwände, $E$ und $F$.

Anwendung des Projektionsverfahren

Um den Abstand von $L$ zu $F$ (oder $E$) zu bestimmen, kannst du das Projektionsverfahren verwenden.Die Hesse-Normalform von $F$ ist:

$F: \frac{1}{13}\begin{pmatrix}12\\0\\-5\end{pmatrix}\circ \left[\begin{pmatrix}x_1\\x_2\\x_3\end{pmatrix}-\begin{pmatrix}0\\0\\0\end{pmatrix}\right]$

Jetzt kannst du $L$ in die Formel zur Berechnung des Abstands einsetzen und nach $x$ auflösen.

$d(F,L)=0{,}5=\left|\frac{1}{13}\begin{pmatrix}12\\0\\-5\end{pmatrix}\circ\begin{pmatrix}2{,}5\\2{,}5\\x\end{pmatrix}\right|$

$0{,}5=\left|\frac{30-5x}{13}\right|$

$\Rightarrow\;\; x=4{,}7$ oder $x=7{,}3$

Für $x=7{,}3$ würde $L$ außerhalb des Zelts liegen, deshalb ist $x=4{,}7$ und $L$ hat die Koordinaten $(2{,}5|2{,}5|4{,}7)$.

Um deine Antwort zu überprüfen, kannst du $L$ in die Hesse-Normalform von $E$ einsetzen.

Lösung zur Teilaufgabe e)

Da $S$ über der Mitte der Grundfläche der Pyramide liegt, ist das Dreieck $CDS$ gleichschenklig mit den Schenkeln $[CS]$ und $[DS]$. Die Symmetrieachse muss also durch $S$ und den Mittelpunkt (hier genannt $M$) der Seite $[CD]$ verlaufen. Stelle eine Gerade durch diese Punkte auf.

Berechnung des Mittelpunkts

$\overrightarrow{M}=\frac{1}{2}\cdot\left(\overrightarrow{C}+ \overrightarrow{D}\right)=\begin{pmatrix}2{,}5\\5\\0\end{pmatrix}$

Berechnung des Richtungsvektors

Als Richtungsvektor kannst du $\overrightarrow{MS}$ verwenden.

$\overrightarrow{MS}=\overrightarrow{S} - \overrightarrow{M}=\begin{pmatrix}0\\-2{,}5\\6\end{pmatrix}$

Aufstellen der Symmetriegerade

Setze den Richtungsvektor und einen Aufpunkt (entweder $M$ oder $S$ in die allgemeine Geradengleichung in der analytischen Geometrie ein.

Lösung zur Teilaufgabe f)

Die Fläche des Vordachs entspricht der Fläche des Eingangs. Eine Seitenlänge dieses Rechtecks ist bekannt ($1{,}4\,\mathrm{m}=1{,}4$ Längeneinheiten), die andere Seitenlänge gilt es zu berechnen. Die Höhe des Eingangs ist $1{,}8\,\mathrm{m}$, also auch $1{,}8$ Längeneinheiten. Da der Eingang symmetrisch zur Symmetriegerade $g$ ist, liegt die unbekannte Seite im rechten Winkel zur Strecke $[CD]$.

Berechne zunächst einen Punkt $P$, der auf $E$ liegt und die Höhe $x_3=1{,}8$ besitzt. Dann kannst du den Abstand von $P$ zu der Gerade $CD$ berechnen. Dieser Abstand ist die Länge der zweiten Seite.

Berechnung von $P$

$P$ hat die Koordinaten $(x_1|x_2|1{,}8)$. Setze diese Koordinaten in die Ebenengleichung von $E$ ein.

Die $x_1$-Koordinate von $P$ kannst du frei wählen ($P$ liegt für jede beliebige $x_1$-Koordinate auf $E$); der Einfachheit halber wurde hier $x_1=0$ gewählt. $P$ hat dann die Koordinaten $(0|4{,}25|1{,}8)$.

Berechnung des Abstands

Hierzu gibt es mehrere Möglichkeiten.

1. Möglichkeit

Bestimme die Gleichung der Gerade $CD$.

$CD: \overrightarrow{x}=\overrightarrow{C}+\lambda\cdot\overrightarrow{CD}$

$CD: \overrightarrow{x}=\begin{pmatrix}5\\5\\0\end{pmatrix}+\lambda\cdot\begin{pmatrix}-5\\0\\0\end{pmatrix}$

Benutze die Formel zur Bestimmung des Abstands.

$d=\frac{\left|\left(\begin{pmatrix} 0 \\ 4{,}25 \\ 1{,}8 \end{pmatrix}-\begin{pmatrix} 5 \\ 5 \\ 0 \end{pmatrix}\right)\times\begin{pmatrix} -5 \\ 0 \\ 0 \end{pmatrix} \right|}{\sqrt{(-5)^2+0^2+0^2}}$

$=\frac{\left|\begin{pmatrix} -5 \\ -0{,}75 \\ 1{,}8 \end{pmatrix}\times\begin{pmatrix} -5 \\ 0 \\ 0 \end{pmatrix} \right|}{5}$

$=\frac{\left|\begin{pmatrix} 0 \\ -9 \\ 3{,}75 \end{pmatrix} \right|}{5}$

$=\frac{\sqrt{(-9)^2+3{,}75^2}}{5}$

$=1{,}95$

2. Möglichkeit

Berechne den Lotpunkt $L$ von $P$ auf $CD$. Da $L$ auf der Gerade $CD$ liegt, ist $x_2=5$ und $x_3=0$. Da $[PL]$ parallel zur Symmetriegerade $g$ liegt, muss $L$ die gleiche $x_1$-Koordinate wie $P$ haben ($\Rightarrow\;\; x_1=0$). $L$ hat also die Koordinaten $(0|5|0)$.Die zweite Seitenlänge ist die Länge der Strecke $[PL]$. $[PL]=\left|\overrightarrow{PQ}\right|=\left|\begin{pmatrix}0\\5\\0\end{pmatrix}-\begin{pmatrix}0\\4{,}25\\1{,}8\end{pmatrix}\right|=1{,}95$

Berechnung des Flächeninhalts

Der Flächeninhalt ist: $A=1{,}95\cdot 1{,}4=2{,}73$