Geometrie, Teil A, Aufgabengruppe 1

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

Die Abbildung zeigt ein gerades Prisma ABCDEF mit $A (0 ∣ 0 ∣ 0)$ , $B (8 ∣ 0 ∣ 0)$ , $C (0 ∣ 8 ∣ 0)$ und $D (0 ∣ 0 ∣ 4)$

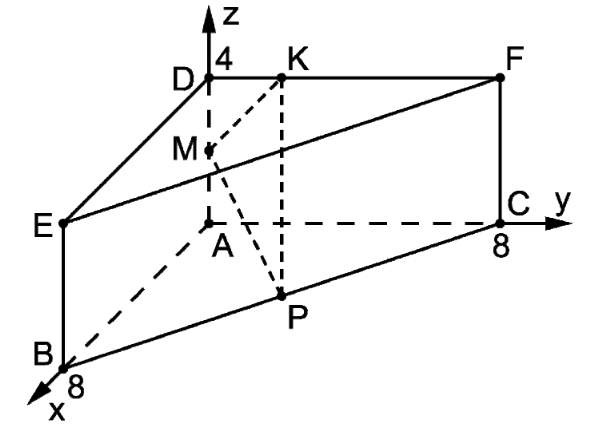
a) Bestimmen Sie den Abstand der Eckpunkte B und F. (2 BE)

b) Die Punkte M und P sind die Mittelpunkte der Kanten $[A D]$ bzw. $[B C]$ . Der Punkt $K (0 ∣ y_{K} ∣ 4)$ liegt auf der Kante $[D F]$ . Bestimmen Sie $y_{K}$ so, dass das Dreieck KMP in M rechtwinklig ist. (3 BE)

Teilaufgabe a)

Für die Bestimmung des Abstandes zweier Punkte ist der Betrag des Differenzvektors zu berechnen - Stichwort: Pythagoras!

$\displaystyle d\left(B,F\right)$	$=$	$\displaystyle \left\|\overrightarrow{BF}\right\|$
	$=$	$\displaystyle \left\|\vec{f}-\vec{b}\right\|$

Spätestens jetzt müssen die Koordinaten von $F$ geklärt werden: Da es sich um eine gerades Prisma handelt, befindet sich der Punkt $F$ 4 Längeneinheiten in $x_{3}$ -Richtung über Punkt $C$ , daher sind die Koordinaten von $F$ : $(0 ∣ 8 ∣ 4)$ .

$\displaystyle d\left(B,F\right)$	$=$	$\displaystyle \left\|\begin{pmatrix}0\\8\\4\end{pmatrix}- \begin{pmatrix}8\\0\\0\end{pmatrix}\right\|$
	$=$	$\displaystyle \left\|\begin{pmatrix}-8\\8\\4\end{pmatrix}\right\|$
	$=$	$\displaystyle \sqrt{(-8)^2+8^2+4^2}$
	$=$	$\displaystyle \sqrt{144}$
	$=$	$\displaystyle 12$

Teilaufgabe b)

Rechtwinkligkeit zwischen zwei Vektoren, weist man am einfachsten nach, in dem man zeigt, dass das entsprechende Skalarprodukt den Wert 0 hat!

Die beiden Schenkel $\overrightarrow{MK}$ und $\overrightarrow{MP}$ werden wie schon in Teilaufgabe a) als Differenvektoren berechnet. Somit ist nun also der Ansatz:

$\displaystyle 0$	$=$	$\displaystyle \begin{pmatrix}0-0\\y_k-0\\4-2\end{pmatrix} \circ \begin{pmatrix}4-0\\4-0\\0-2\end{pmatrix}$
$\displaystyle 0$	$=$	$\displaystyle \begin{pmatrix}0-0\\y_k-0\\4-2\end{pmatrix} \circ \begin{pmatrix}4-0\\4-0\\0-2\end{pmatrix}$
$\displaystyle 0$	$=$	$\displaystyle \begin{pmatrix}0\\y_k\\2\end{pmatrix} \circ \begin{pmatrix}4\\4\\-2\end{pmatrix}$
$\displaystyle 0$	$=$	$\displaystyle 4y_k-4$
$\displaystyle y_k$	$=$	$\displaystyle 1$

Wenn der Punkt $K$ die Koordinaten $(0 ∣ 1 ∣ 4)$ hat, hat das Dreieck $K M P$ bei $M$ einen rechten Winkel!

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Die Abbildung zeigt ein gerades Prisma $A B C D E F$ mit $A (0 ∣ 0 ∣ 0)$ , $B (8 ∣ 0 ∣ 0)$ , $C (0 ∣ 8 ∣ 0)$ und $D (0 ∣ 0 ∣ 4)$
1. Bestimmen Sie den Abstand der Eckpunkte $B$ und $F$ . (2 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Abstand zweier Punkte
  Für die Bestimmung des Abstandes zweier Punkte ist der Betrag des Differenzvektors zu berechnen - Stichwort: Pythagoras!
  $\def\arraystretch{1.25} \begin{aligned} d(B,F) &= \\ &= \left|\overrightarrow{BF}\right| \\ &= \left|\vec{f}-\vec{b}\right| \end{aligned}$
  Spätestens jetzt müssen die Koordinaten von $F$ geklärt werden: Da es sich um eine gerades Prisma handelt, befindet sich der Punkt $F$ 4 Längeneinheiten in $x_{3}$ -Richtung über Punkt $C$ , daher sind die Koordinaten von $F$ : $(0 ∣ 8 ∣ 4)$ .
  $\def\arraystretch{1.25} \begin{aligned} d(B,F) &= \left|\begin{pmatrix}0\\8\\4\end{pmatrix}- \begin{pmatrix}8\\0\\0\end{pmatrix}\right| \\ &= \left|\begin{pmatrix}-8\\8\\4\end{pmatrix}\right| \\ &= \sqrt{(-8)^2+8^2+4^2} =\sqrt{144}\\ &= 12\end{aligned}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Die Punkte M und P sind die Mittelpunkte der Kanten $[A D]$ bzw. $[B C]$ . Der Punkt $K (0 ∣ y_{K} ∣ 4)$ liegt auf der Kante $[D F]$ . Bestimmen Sie $y_{K}$ so, dass das Dreieck KMP in M rechtwinklig ist. (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Abstand zweier Punkte
  Rechtwinkligkeit zwischen zwei Vektoren, weist man am einfachsten nach, in dem man zeigt, dass das entsprechende Skalarprodukt den Wert 0 hat!
  Die beiden Schenkel $\overrightarrow{MK}$ und $\overrightarrow{MP}$ werden wie schon in Teilaufgabe a) als Differenvektoren berechnet. Somit ist nun also der Ansatz:
  $\def\arraystretch{1.25} \begin{aligned} \begin{pmatrix}0-0\\y_k-0\\4-2\end{pmatrix} \circ \begin{pmatrix}4-0\\4-0\\0-2\end{pmatrix} &= 0 \\ \begin{pmatrix}0-0\\y_k-0\\4-2\end{pmatrix} \circ \begin{pmatrix}4-0\\4-0\\0-2\end{pmatrix} &= 0 \\ \begin{pmatrix}0\\y_k\\2\end{pmatrix} \circ \begin{pmatrix}4\\4\\-2\end{pmatrix} &= 0 \\ 4y_k-4&=0 \\ y_k&=1\end{aligned}$
  Wenn der Punkt $K$ die Koordinaten $(0 ∣ 1 ∣ 4)$ hat, hat das Dreieck $K M P$ bei $M$ einen rechten Winkel!
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Gegeben ist die Ebene $E : 3 x_{2} + 4 x_{3} = 5$ .
1. Beschreiben Sie die besondere Lage von $E$ im Koordinatensystem. (1 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Koordinatensystem
  Wenn bei Ebenen nach ihrer besonderen Lage gefragt ist, achtet man auf Koordinaten, die nicht vorkommen, bzw. deren Koeffizient Null ist. Das ist hier mit $x_{1}$ der Fall. Das heißt nicht, dass es diese Koordinage nicht gibt, sondern dass der Wert von $x_{1}$ mit Null multipliziert wird und damit unabhängig vom Wert von $x_{1}$ stets der Beitrag Null in der Koordinatengleichung auftaucht.
  Die beschriebene Punktmenge ist also unabhängig von der Koordinate für $x_{1}$ oder nochmal anders gesagt: Egal welche Puntkmenge beschrieben wird, man kann sie sich an jede $x_{1}$ Position kopiert denken, in der Sprache der 3D-Programme wird hierfür das Wort extrudieren verwendet.
  Die Punktmenge selbst wird durch einen linearen Zusammenhang zwischen $x_{3}$ und $x_{2}$ beschrieben.
  $\def\arraystretch{1.25} \begin{array}{rcll}3x_2+4x_3 &= & 5 &|\text{Ersetze } x_3 \text{ durch } y \\ & & &|\text{Ersetze } x_2 \text{ durch } x \\3x+4y &=&5& \\ y &=& -\frac34 x+\frac54& \end{array}$
  Durch diese kleine Umformung sieht man: Die Punktmenge ist eine Gerade. Und diese Punktmenge wird nun parallel zur $x_{1}$ Richtung kopiert. Dadurch entsteht eine Ebene.
  Kurz gesagt: Fehlt die Koordinate $x_{i}$ handelt es sich um einen Ebene, die parallel zur $x_{i}$ -Achse verläuft!
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Untersuchen Sie rechnerisch, ob die Kugel mit Mittelpunkt $Z (1 ∣ 6 ∣ 3)$ und Radius $7$ die Ebene $E$ schneidet. (4 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Kugel
  Hier denkt man an Kugelgleichungen und Schnittmengen, aber man kommt glimpflich davon. Die Zeichnung ist zwar nicht gefordert, aber das nächste Bild zeigt die tatsächliche Lage der Ebene und der Kugel:
  Ob es einen Schnittmenge zwischen Ebene und Kugel gibt, hängt von der Länge der rot eingezeichneten Strecke $[M Z]$ ab, wobei hier $M$ der Mittelpunkt des enstehenden Schnittkreises ist.
  Letztlich geht es also um den Abstand des Punktes $Z$ von der Ebene $E$ .
  Tatsächlich ist in dieser Aufgabe also die Berechnung des Abstandes eines Punktes von einer Ebene gefordert. Die Standardlösung besteht aus 2 Schritten:
  Schritt 1: Hesse-Normalenform der Ebene herstellen:
  Ein Normalenvektor $\vec{n}$ der Ebene kann aus den Koordinaten abgelesen werden: $\vec{n}=\begin{pmatrix}0\\3\\4\end{pmatrix}$ . Der Normalenvektor hat die Länge: $\left|\vec{n}\right|=\sqrt{3^2+4^2}=5$ . Daher wird die Koordinatenform mit $\frac15$
  $\def\arraystretch{1.25} \begin{aligned} E: 3x_2+4x_3 -5 &= 0 \\\frac15( 3x_2+4x_3 -5) &= 0 \end{aligned}$
  Schritt 2: Abstandsberechnung mit der Hesse-Normalen-Form
  Der Abstand $d (Z, E)$ ergibt sich als Betrag des Wertes der linken Seite der Gleichung, wenn man dort die Koordinaten des Punktes $Z$ einsetzt: $d(Z,E)=\left|\frac15(0\cdot 1+ 3\cdot6+4\cdot 3 -5)\right| = \left|5\right| =5$ .
  Dieses Ergebnis ist mit dem Radius der Kugel $r = 7$ zu vergleichen: Wegen $d (Z, E) < r$ , ergibt sich eine nichtleere Schnittmenge, ein Schnittkreis.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Geometrie, Teil A, Aufgabengruppe 1

Teilaufgabe a)

Teilaufgabe b)

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Schritt 1: Hesse-Normalenform der Ebene herstellen:

Schritt 2: Abstandsberechnung mit der Hesse-Normalen-Form

Hast du eine Frage oder Feedback?