Aufgaben zu indirekt proportionalen Zuordnungen
- 1
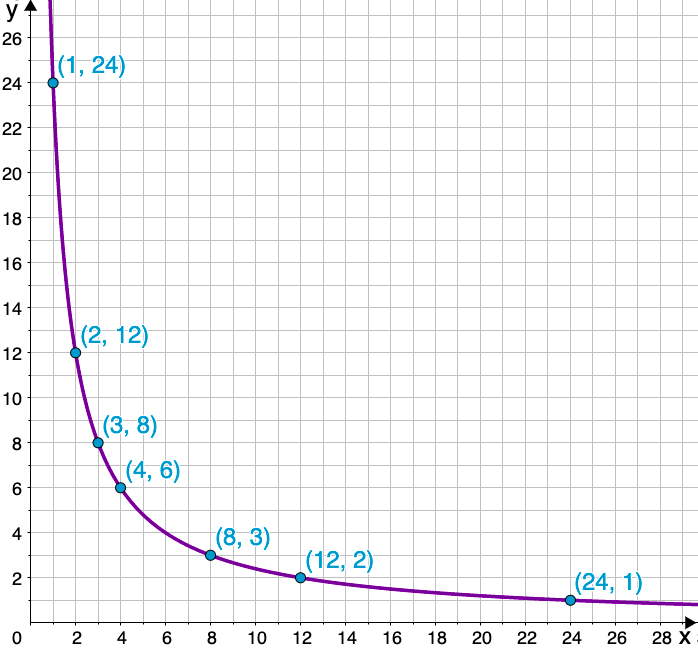
Um ein Rechteck mit einem Flächeninhalt von zu erhalten, kannst du die Länge (x in cm) und Breite (y in cm) der Seiten des Rechtecks unterschiedlich wählen.
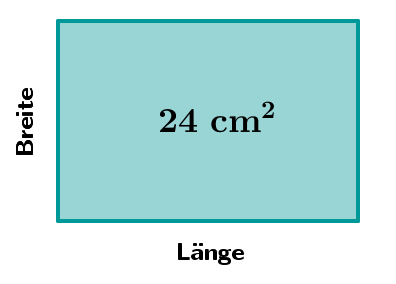
a) Bestimme alle ganzzahligen Paare aus Länge und Breite, die ein Rechteck mit einem Flächeninhalt von ergeben. Trage die Wertepaare in eine Wertetabelle ein.
b) Stelle mit Hilfe der Tabelle den Zusammenhang der beiden Größen graphisch dar.
c) Bestimme nun den zum Graphen zugehörigen Funktionsterm. Vewende dazu die Formel für den Flächeninhalt eines Rechtecks.
- 2
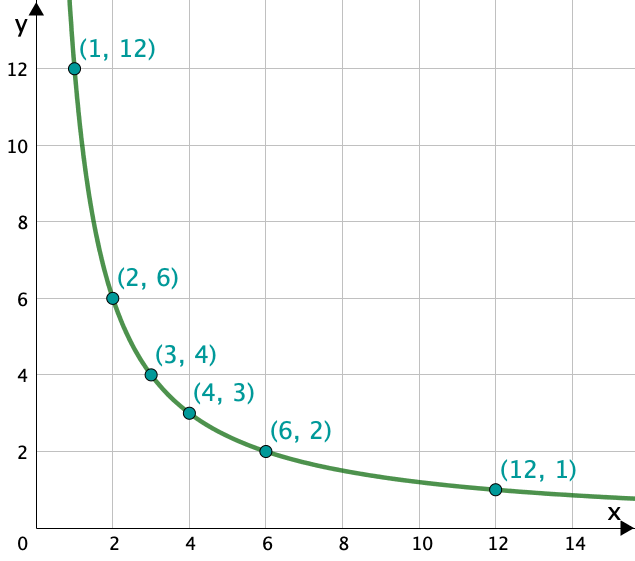
Um den Zusammenhang zwischen der Grundlinie und der zugehörigen Höhe eines Dreiecks mit Flächeninhalt darzustellen, kannst du die Länge (x in cm) der Grundlinie und die Höhe (y in cm) unterschiedlich wählen.
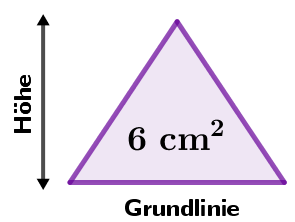
a) Bestimme alle ganzzahligen Paare aus Grundlinie (Grundseite) und zugehörige Höhe, die ein Dreieck mit einem Flächeninhalt von ergeben. Trage die Werte in eine Tabelle ein.
b) Stelle mit Hilfe der Tabelle den Zusammenhang zwischen Grundseite und Höhe dar. Warum darf man die Punkte verbinden, wenn auch andere als ganzzahlige Paare zugelassen werden?
c) Bestimme nun die zugehörige Funktion des Graphen. Betrachte dazu die Formel für den Flächeninhalt eines Dreiecks.
- 3
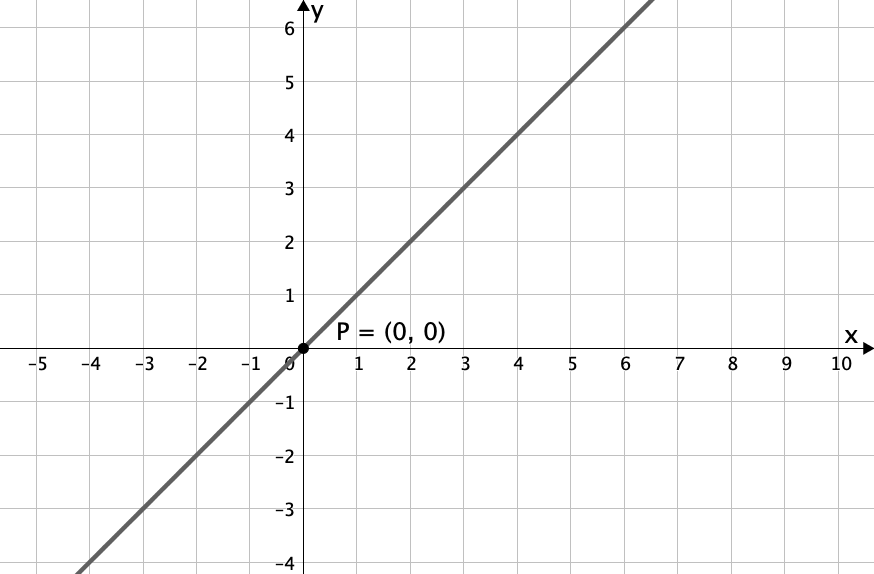
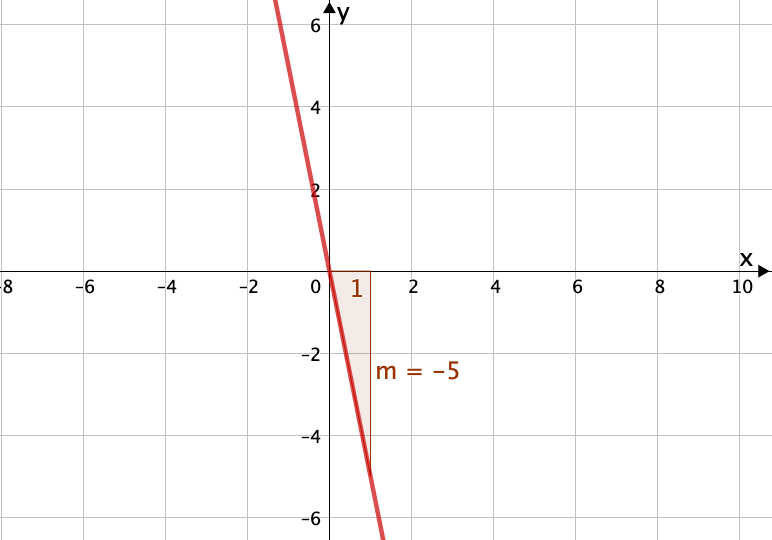
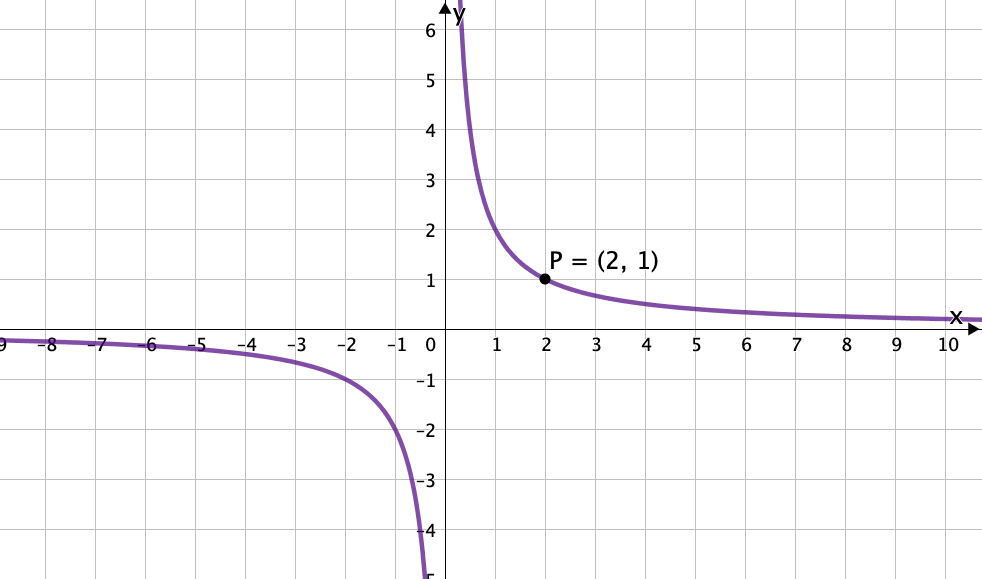
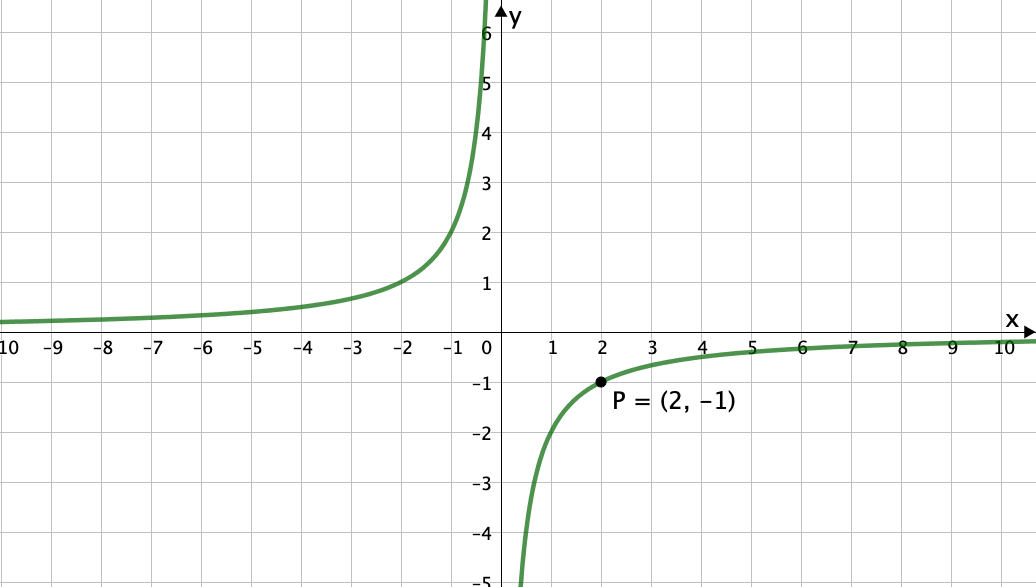
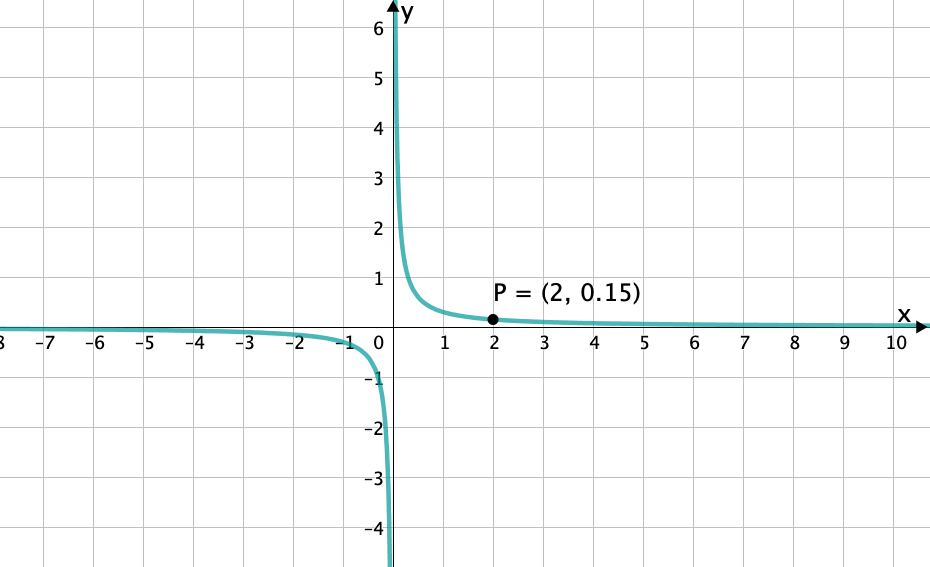
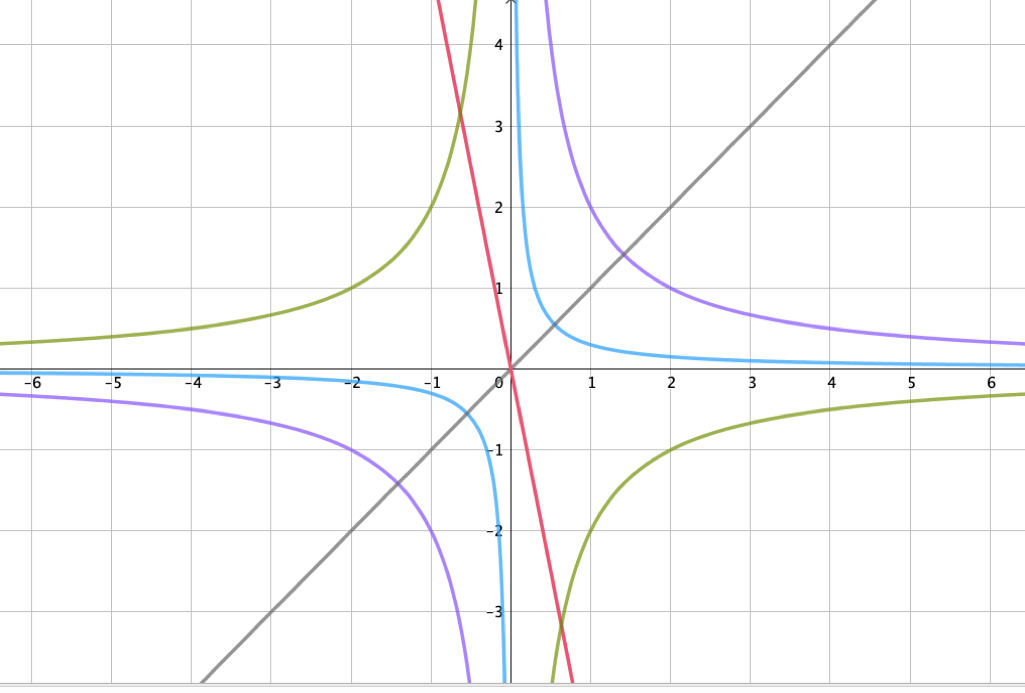
Ordne jedem der Funktionsgraphen die passende Funktion zu.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?