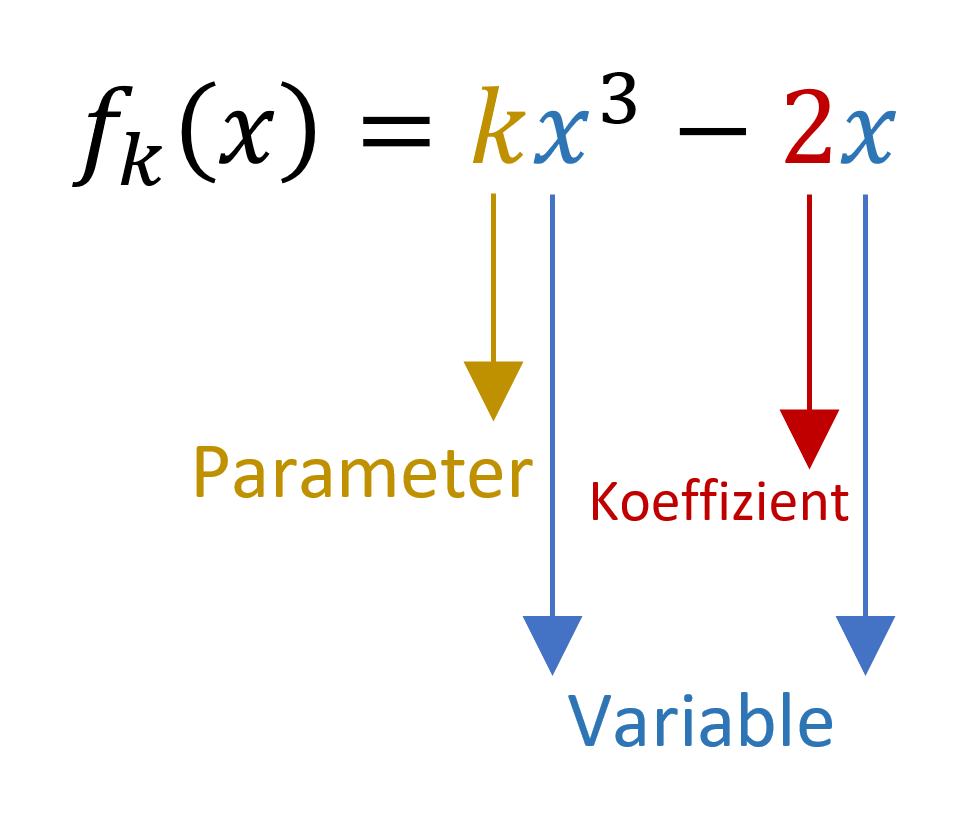
Ein Parameter ist eine Variable, die zusammen mit der Funktionsvariablen auftritt.
Ein Koeffizient ist ein Faktor, der zu einer Variable gehört. Ein Koeffizient kann auch ein Parameter sein.
Parameter
Ein Parameter, meist mit oder bezeichnet, ist ähnlich einer Variablen nicht auf einen bestimmten Wert festgelegt. Trotzdem wird mit ihm wie mit einem festen Wert gerechnet.
Beispiel:
In der Funktion ist ein Parameter und die Variable. Manchmal wird der Parameter einer Funktion als Index notiert: statt
Bei der allgemeinen quadratischen Funktion sind Parameter. Diese nehmen in einer bestimmten quadratischen Funktion einen festen Wert an (z.B. ).
Koeffizient
Ein Koeffizient ist ein Faktor, der zu einer Variablen oder einem Vektor gehört.
Beispiel:
Bei der Funktion ist die ein Koeffizient, jedoch kein Parameter, denn der Wert ist fest definiert.
Bei der obigen Funktion ist sowohl der Koeffizient, als auch ein Parameter, da das veränderlich ist.
Unterschied zwischen Parameter und Variable
Ändert sich der Wert einer Variablen, verändern sich die Funktionswerte. Ändert sich hingegen ein Parameter, verändert sich der Verlauf des Funktionsgraphen.
Beispiel:
Verändern wir bei der Funktion den Wert der Variablen, so erhalten wir unterschiedliche Funktionswerte:
Verändern wir hingegen bei der Funktion die Werte, die der Parameter annimmt, verändert sich der Verlauf der Funktion:
Wir setzen
Der Index in ändert sich deshalb zu einer .
Für erhalten wir
und sind zwar beide Geraden, haben allerdings unterschiedliche Verläufe. Führt man diese Rechnung noch für und durch und zeichnet dann alle Geraden in ein Koordinatensystem ein, erhält man die folgende Abbildung:
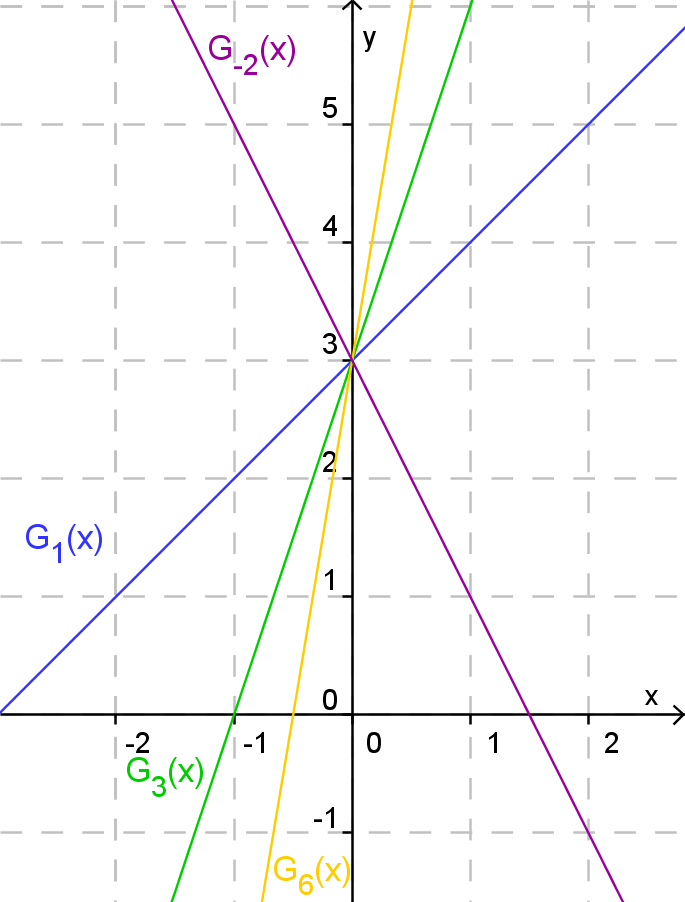
Die Funktion ist eine Funktionenschar. Durch Variation des Parameters erhält man unterschiedliche Funktionsverläufe.
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
