Aufgaben zur Kurvendiskussion
Setze hier alle Bestandteile zusammen und übe mit Aufgaben zur Kurvendiskussion.
- 1
Es ist folgende Funktion gegeben:
In den Teilaufgaben findest du alles, was du für diese Funktion berechnen könntest.
Suche dir das heraus, was du üben möchtest.
Bei späteren Teilaufgaben kann auf frühere Ergebnisse zurückgegriffen werden.
Ist dir nicht sofort klar, woher diese Ergebnisse kommen, dann bearbeite zunächst diese früheren Teilaufgaben zur Wissensauffrischung.
Bestimme den Definitionsbereich und die Art der Definitionslücken.
Vereinfache die Funktionsgleichung.
Berechne die Grenzwerte an den Rändern des Definitionsbereichs.
Setze die Funktion - wenn möglich - stetig zu einer Funktion fort.
Bestimme die Asymptoten.
Bestimme die Nullstellen.
Bestimme die Extrempunkte.
Bestimme das Monotonieverhalten.
Berechne die Wendepunkte.
Bestimme das Krümmungsverhalten.
Berechne den Wertebereich.
Zeichne den Graph.
Überprüfe das Symmetrieverhalten.
Bestimme die Tangente zur Funktion am allgemeinen Punkt .
Bestimme die Schnittpunkte des Funktionsgraphen von mit dem Funktionsgraphen von der Funktion
Berechne die Stammfunktion.
Bestimme die Größe der Fläche zwischen dem Graphen der Funktion , der x-Achse und den Geraden und .
Bestimme die Größe der Fläche die der Graph der stetigen Funktion mit dem Graphen der Tangente von am Punkt einschließt.
Hinweis: Runde die Integrationsgrenzen und das Ergebnis auf zwei Nachkommastellen
Berechne den Umfang und den Flächeninhalt des Vierecks
Runde Zwischenergebnisse notfalls auf zwei Nachkommastellen.
Das ist keine typische Analysisaufgabe, sondern eher ein kurzer Abstecher in die Geometrie. Willst du nur Analysis üben, dann kannst du diese Aufgabe gerne ignorieren.
- 2
Es ist folgende Funktionenschar gegeben:
In den Teilaufgaben findest du vieles, das du für diese Funktion berechnen kannst.
Suche dir heraus, was du üben möchtest.
Die Teilaufgaben sind in einer logischen Reihenfolge angeordnet, daher wird in späteren Aufgaben auf Ergebnisse von früher zurückgegriffen.
Wenn dir nicht klar ist, woher diese Ergebnisse kommen, dann rechne am besten die zugehörige Teilaufgabe davor nach.
Definitionsbereich bestimmen
Grenzwertbetrachtungen: Bestimme die Grenzwerte an allen Grenzen des Definitionsbereichs.
Asymptoten bestimmen
Nullstellen bestimmen
Symmetrieverhalten überprüfen
Monotonieverhalten bestimmen
Krümmungsverhalten bestimmen
Extremwerte bestimmen
Wertebereich bestimmen
Tangente bestimmen:
Bestimme die Tangente an den Funktionsgraphen von , die für auch durch den Punkt geht und für durch den Punkt .
Stammfunktion I:
Zeige, dass
eine Stammfunktion von für ist.
Stammfunktion II:
Bestimme durch Rechnung die Stammfunktion von .
Achtung, diese Integration ist etwas schwieriger und erfordert mehr Überlegungen und Rechenschritte, als in der Schule normalerweise verlangt werden. Wer allerdings ein paar Tricks beim Integrieren ausprobieren/lernen will kann die Aufgabe gerne bearbeiten oder sich die Lösung anschauen.
Für alle Anderen reicht es, die Aufgabe "Stammfunktion I" zu bearbeiten, die normalem Schulniveau entspricht.
Flächenberechnung I:
Berechne die Fläche, die der Funktionsgraph mit den Koordinatenachsen einschließt.
Flächenberechnung II:
Berechne die Fläche die von der x-Achse, den Geraden und dem Graphen von eingeschlossen wird.
Graphen zeichnen:
Zeichne folgende Graphen für in ein oder mehrere Koordinatensysteme:
mit seinen Asymptoten und
- 3
Es ist folgende Funktion gegeben:
In den folgenden Teilaufgaben werden verschiedene Teile einer Kurvendiskussion abgefragt.
Suche dir das heraus, was du üben möchtest.
Bei späteren Teilaufgaben kann auf frühere Ergebnisse zurückgegriffen werden.
Ist dir nicht sofort klar, woher diese Ergebnisse kommen, dann bearbeite zunächst diese früheren Teilaufgaben zur Wissensauffrischung.
Bestimme den maximalen Definitionsbereich der Funktion.
Bestimme die Schnittpunkte mit den Koordinatenachsen.
Gib die Asymptoten der Funktion an.
Überprüfe die Funktion auf Achsensymmetrie bezüglich der y-Achse und Punktsymmetrie zum Ursprung.
Bestimme die Tangente an die Funktion an der Stelle
Hat die Funktion Extremstellen? Bestimme sie gegebenenfalls.
- 4
Im Labor wird eine Maispflanze beobachtet, um den Wachstumsverlauf zu erforschen. Dazu beginnen die Forscher ihre Aufzeichnungen mit einem Setzling zum Zeitpunkt t=0 und messen die Höhe der Pflanze kontinuierlich über die nächsten sieben Monate.
Die folgende Funktion konnten die Forscher dabei aufzeichnen:
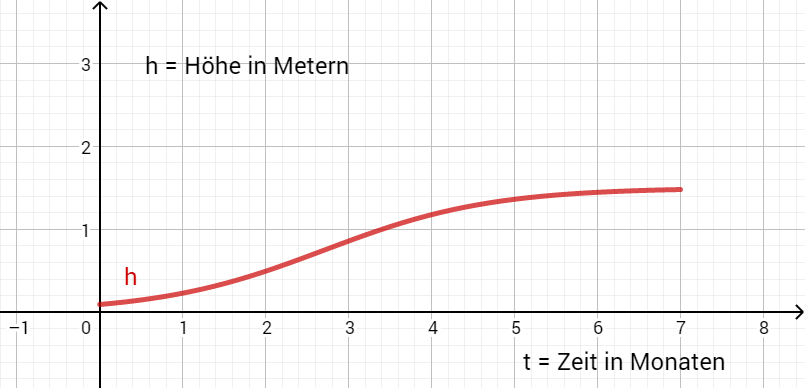
Die Funktion kann modellhaft durch die Funktion beschrieben werden.
Dabei ist die Zeit in Monaten, die seit Beobachtungsbeginn vergangen ist.
ist die Höhe zur Zeit in Metern, die die Maispflanze groß ist.
Berechne die Größe in Zentimeter des Setzlings zu Beginn der Beobachtung!
Berechne, wie viele Zentimeter die Maispflanze in den ersten sechs Wochen nach Aufzeichnungsbeginn gewachsen ist!
Zu welchem Zeitpunkt ist das Wachstum der Pflanze maximal?
Bestimme die Wachstumsrate zu diesem Zeitpunkt in Zentimeter pro Tag!
Bestimme die maximal zu erreichende Höhe dieser Maissorte, indem du den Grenzwert von h(x) gegen Unendlich betrachtest.
Wie müsste die passende Funktionsgleichung aussehen, wenn die Pflanze zu Anfang dieselbe Höhe hätte, also , aber jede weitere Höhe von exakt in der Hälfte der Zeit von erreicht wird ?
Betrachte Teilaufgabe . Begründe, warum die anderen beiden Antworten nicht richtig sein können!
Betrachte Teilaufgabe . Gebe den entsprechenden Wert von an!
- 5
Die Abbildung zeigt den Graphen der Funktion .
Gib den maximalen Definitionsbereich der Funktion an.
Berechne die Nullstellen.
Skaliere in der Abbildung die Koordinatenachsen.
Bestimme die Koordinaten des Hochpunktes von g.
Die Untersuchung der notwendigen Bedingung ist ausreichend.
- 6
ist der achsensymmetrische Graph einer Funktion 4. Grades.
Erläutere nur unter Bezugnahme auf Symmetrie und Globalverlauf des Graphen, warum nur Funktionsterm infrage kommt.
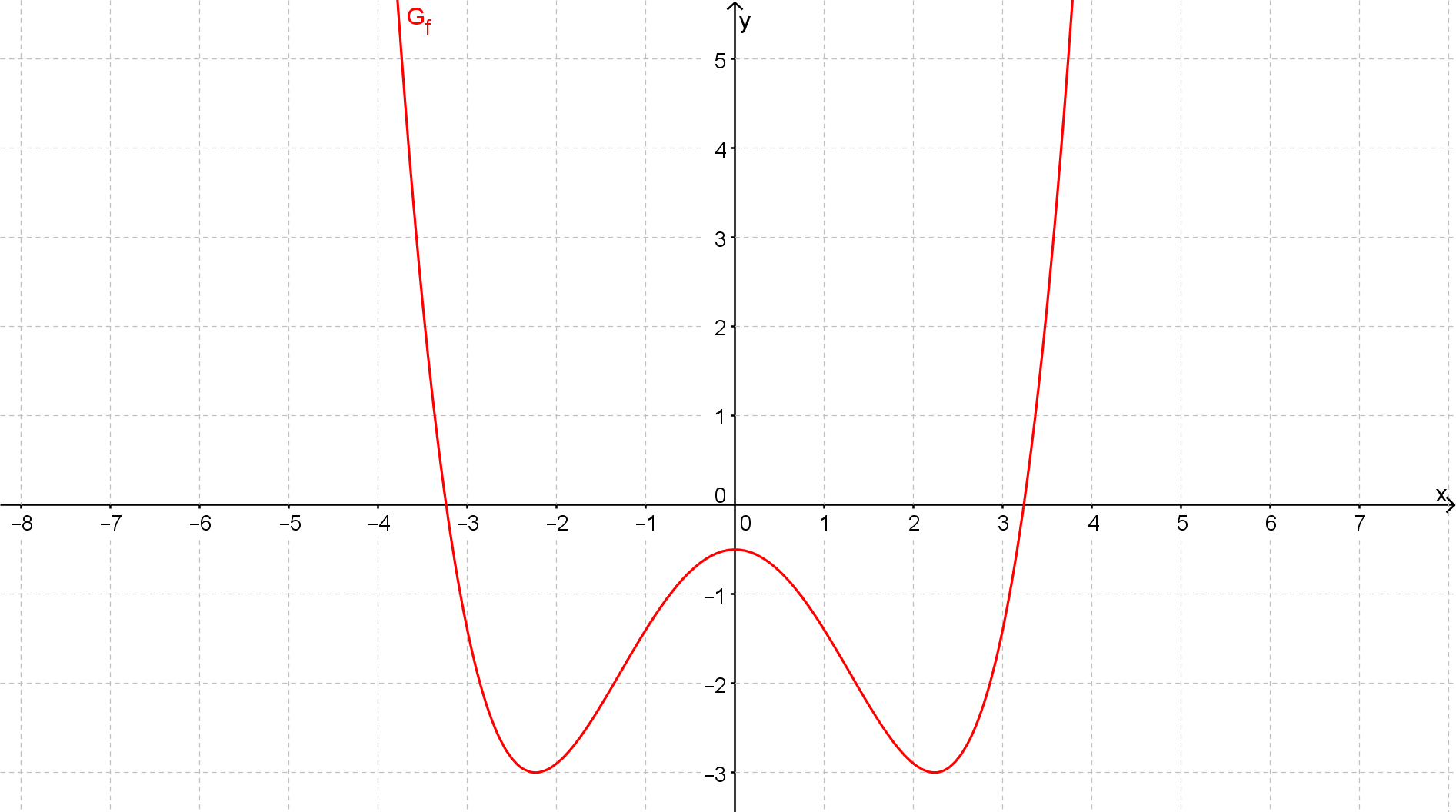
- 7
Graphenzuordnung
- 8
Um das Monotonieverhalten (steigend/fallend) und das Krümmungsverhalten (links- oder rechtsgekrümmt) zu untersuchen, kannst du ähnliche Methoden verwenden.
In dieser Aufgabe sollst du dir Gedanken über die Gemeinsamkeiten und Unterschiede machen.
Egal, ob du später eine Skizze oder eine Tabelle anfertigen wirst (oder sogar mit einer höheren Ableitung arbeiten wirst), zunächst musst du Vorarbeit leisten.
Vergleiche, wie du die Kandidaten für Extrem- und Wendestellen bekommst.
Du untersuchst das Monotonie- und Krümmungsverhalten mithilfe einer Skizze. Wodurch unterscheiden sich die Skizzen zur Monotonie und zur Krümmung?
Statt mit einer Skizze kannst du das Monotonie- und Krümmungsverhalten auch mithilfe von Tabellen untersuchen. Wodurch unterscheiden sich die Monotonietabelle und die Krümmungstabelle voneinander?
- 9
Gegeben ist die Funktion mit und dem Graph .
Bestimme die Art und Lage des Extrempunktes.
Untersuche, ob der Graph Wendepunkte besitzt und gib sein Krümmungsverhalten an. Folgere daraus, ob es Stellen stärkster Zu- oder Abnahme gibt.
Bestimme die Schnittpunkte mit den Koordinatenachsen.
Gib den Globalverlauf von f für an.
Zeichne den Graphen für , wobei auf beiden Achsen gilt.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

