Aufgaben zur Kurvendiskussion - lernen mit Serlo!

Gegeben ist die Funktion $f (x) = e^{x^{2} - 2 x}$ mit $D_{f} = ℝ$ und dem Graph $G_{f}$ .

Bestimme die Art und Lage des Extrempunktes.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen
Ableitungsfunktion bestimmen
Du benötigst die Kettenregel, da du eine e-Funktion ableiten musst.
$f^{'} (x) = (2 x - 2) e^{x^{2} - 2 x}$
Nullstellen der Ableitung
Die Kandidaten für Extremstellen von $f$ liegen bei den Nullstellen von $f^{'}$ :
$f^{'} (x)$ $=$ $0$
$(2 x - 2) e^{x^{2} - 2 x}$ $=$ $0$
↓
Nach dem Satz vom Nullprodukt kann man die Faktoren einzeln betrachten. Dabei liefert $e^{x^{2} - 2 x}$ keine Nullstellen, da $e^{x} > 0$ für alle x.
$2 x - 2$ $=$ $0$ $+ 2$
$2 x$ $=$ $2$ $: 2$
$x$ $=$ $1$
Da die Nullstelle die Vielfachheit 1 hat, wird bei $x = 1$ eine Extremstelle von f liegen.
Art der Extremstelle
Leite $f^{'} (x) = (2 x - 2) e^{x^{2} - 2 x}$ nochmal ab, um die Art der Extremstelle mit der 2. Ableitung zu bestimmen. Du brauchst nun zusätzlich die Produktregel.
$f^{''} (x)$ $=$ $2 \cdot e^{x^{2} - 2 x} + (2 x - 2) \cdot (2 x - 2) e^{x^{2} - 2 x}$
↓
Klammere $e^{x^{2} - 2 x}$ aus
$=$ $e^{x^{2} - 2 x} \cdot (2 + {(2 x - 2)}^{2})$
↓
Multipliziere mit der binomischen Formel aus.
$=$ $e^{x^{2} - 2 x} \cdot (2 + 4 x^{2} - 8 x + 4)$
$=$ $e^{x^{2} - 2 x} \cdot (4 x^{2} - 8 x + 6)$
Setze deinen gefundenen Kandidaten $x = 1$ in die 2. Ableitung ein:
$f^{''} (1) = e^{- 1} \cdot 2 > 0$ und somit liegt bei $x = 1$ ein Tiefpunkt.
Lage der Extremstelle
Setze $x = 1$ in f ein, um den zugehörigen Funktionswert zu bestimmen:
$f (1) = e^{- 1} = \frac{1}{e}$
Der Graph hat also den Tiefpunkt $T I P (1 | \frac{1}{e})$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Um die Art und Lage eines Extrempunktes zu bestimmen, musst du folgende Schritte ausführen:
Bilde die erste Ableitung $f^{'}$
Bestimme die Nullstellen von $f^{'}$
Bestimme die Art der Extremstelle über die Monotonietabelle oder die 2. Ableitung
Setze in den Term von $f$ ein, um die y-Koordinate des Extrempunktes zu ermitteln.
Untersuche, ob der Graph Wendepunkte besitzt und gib sein Krümmungsverhalten an. Folgere daraus, ob es Stellen stärkster Zu- oder Abnahme gibt.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Krümmungsverhalten eines Funktionsgraphen
Nullstellen der zweiten Ableitung
In der ersten Teilaufgabe hast du bereits die zweite Ableitung bestimmt. Suche jetzt nach ihren Nullstellen.
$f^{''} (x)$ $=$ $0$
$e^{x^{2} - 2 x} \cdot (4 x^{2} - 8 x + 6)$ $=$ $0$
↓
Nach dem Satz vom Nullprodukt kann jeder Faktor einzeln betrachtet werden. $e^{x^{2} - 2 x}$ hat allerdings keine Nullstellen, da $e^{x} > 0$ für alle $x \in ℝ$
$4 x^{2} - 8 x + 6$ $=$ $0$
Verwende die Mitternachtsformel, um die Lösungen der Gleichung zu bestimmen:
$x_{1 / 2} = \frac{- (- 8) \pm \sqrt{(- 8)^{2} - 4 \cdot 4 \cdot 6}}{2 \cdot 4} = \frac{8 \pm \sqrt{- 32}}{8}$
Da die Diskriminante $D = - 32$ negativ ist, gibt es keine Lösungen.
Somit hat der Graph keine Wendepunkte.
Krümmungsverhalten
Es gibt keine Wendepunkte. Also hat der Graph auf der gesamten Definitionsmenge die gleiche Krümmung.
Du kannst eine beliebige Zahl einsetzen, um diese Krümmung herauszufinden:
$f^{''} (0) = 6 > 0$ also ist der Graph für alle $x \in ℝ$ linksgekrümmt.
Stellen stärkster Zu- oder Abnahme
Da der Graph keine Wendepunkte hat, kann es keine Stellen lokal stärkster Zu- oder Abnahme geben.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Für die Bestimmung von Wendepunkte und Krümmungsverhalten gehst du folgendermaßen vor:
Bestimme die 2. Ableitung
Bestimme die Nullstellen der 2. Ableitung. Falls es keine gibt, gibt es keine Wendepunkte
Das Krümmungsverhalten hängt vom Vorzeichen der 2. Ableitung ab. Falls es Wendepunkte gibt, fertige eine Krümmungstabelle an.
Die notwendige Vorraussetzung für eine Stelle stärkster Zu- oder Abnahme ist ein Wendepunkt.
Bestimme die Schnittpunkte mit den Koordinatenachsen.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte mit den Koordinatenachsen
Schnittpunkt mit der y-Achse
Setze $x = 0$ ein.
$f (0) = e^{0^{2} - 2 \cdot 0} = e^{0} = 1$
Der Schnittpunkt ist $S_{y} (0 | 1)$
Schnittpunkte mit der x-Achse
Setze mit 0 gleich.
$f (x)$ $=$ $0$
$e^{x^{2} - 2 x}$ $=$ $0$
Diese Gleichung hat keine Lösung, denn $e^{x} > 0$ für alle $x \in ℝ$ und somit hat auch jede andere Exponentialfunktion $e^{g (x)}$ (mit $g (x)$ ganzrationale Funktion) keine Nullstellen.
Es gibt keine Schnittpunkte mit der x-Achse.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Für den Schnittpunkt mit der y-Achse musst du $x = 0$ einsetzen
Für die Schnittpuntke mit der x-Achse musst du den Term mit 0 gleichsetzen, also $f (x) = 0$
Vergiss nicht, die Koordinaten als Punkte anzugeben!
Gib den Globalverlauf von f für $x \to \pm \infty$ an.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Grenzwertbetrachtung
Arbeite dich vom Exponenten aus vor:
$\lim_{x \to - \infty} f (x)$ $=$ $\lim_{x \to - \infty} (e^{x^{2} - 2 x})$
↓
Im Exponenten dominiert $" (- \infty)^{2} " = " + \infty "$
$=$ $\lim_{x \to - \infty} (e^{" + \infty "})$
↓
Verlauf der natürlichen Exponentialfunktion
$=$ $+ \infty$
Für $x \to + \infty$ kannst du genauso vorgehen:
$\lim_{x \to + \infty} f (x)$ $=$ $\lim_{x \to + \infty} (e^{x^{2} - 2 x})$
↓
Im Exponenten dominiert $" (+ \infty)^{2} " = " + \infty "$
$=$ $\lim_{x \to - \infty} (e^{" + \infty "})$
↓
Verlauf der natürlichen Exponentialfunktion
$=$ $+ \infty$
Der Graph hat also keine Asymptoten.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Betrachte zuerst das Verhalten des Exponenten und dann das Verhalten der Exponentialfunktion.
Zeichne den Graphen $G_{f}$ für $x \in [0; 2,5]$ , wobei auf beiden Achsen $2 c m \hat{=} 1 L E$ gilt.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Graph einer Funktion
Fertige eine Wertetabelle für f mit den Grenzen 0 und 2,5 und der Schrittweite 0,25 an.
In deinem Koordinatensystem ist auf beiden Achsen erst bei 2cm die Zahl 1 anzutragen:
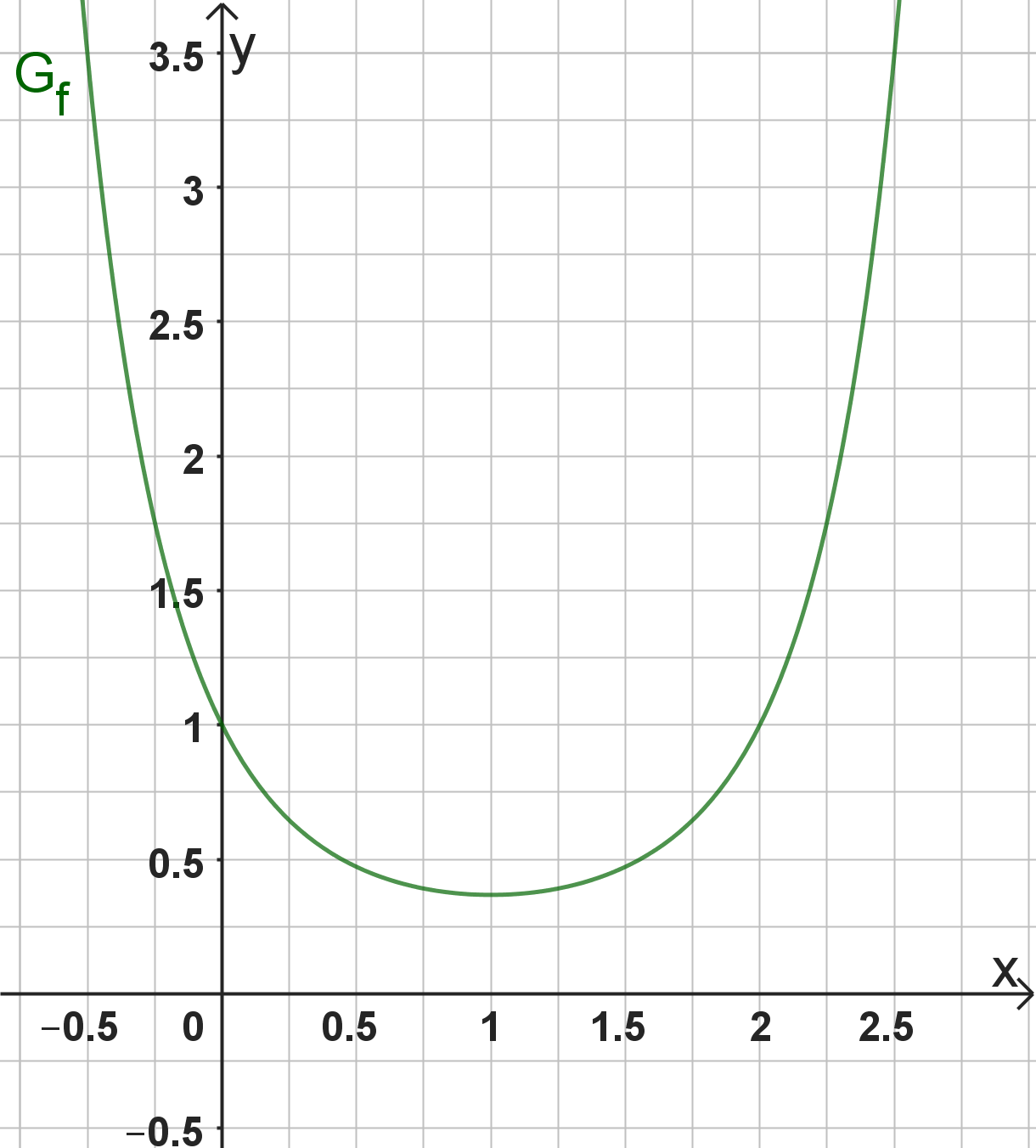
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Fertige eine Wertetabelle an und wähle die Schrittweite 0,25. So kannst du bei jedem Kästchen einen Punkt einzeichnen und erhältst ein genau genuges Ergebnis.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$f^{'} (x)$	$=$	$0$
$(2 x - 2) e^{x^{2} - 2 x}$	$=$	$0$
	↓	Nach dem Satz vom Nullprodukt kann man die Faktoren einzeln betrachten. Dabei liefert $e^{x^{2} - 2 x}$ keine Nullstellen, da $e^{x} > 0$ für alle x.
$2 x - 2$	$=$	$0$	$+ 2$
$2 x$	$=$	$2$	$: 2$
$x$	$=$	$1$

$f^{''} (x)$	$=$	$2 \cdot e^{x^{2} - 2 x} + (2 x - 2) \cdot (2 x - 2) e^{x^{2} - 2 x}$
	↓	Klammere $e^{x^{2} - 2 x}$ aus
	$=$	$e^{x^{2} - 2 x} \cdot (2 + {(2 x - 2)}^{2})$
	↓	Multipliziere mit der binomischen Formel aus.
	$=$	$e^{x^{2} - 2 x} \cdot (2 + 4 x^{2} - 8 x + 4)$
	$=$	$e^{x^{2} - 2 x} \cdot (4 x^{2} - 8 x + 6)$

$f^{''} (x)$	$=$	$0$
$e^{x^{2} - 2 x} \cdot (4 x^{2} - 8 x + 6)$	$=$	$0$
	↓	Nach dem Satz vom Nullprodukt kann jeder Faktor einzeln betrachtet werden. $e^{x^{2} - 2 x}$ hat allerdings keine Nullstellen, da $e^{x} > 0$ für alle $x \in ℝ$
$4 x^{2} - 8 x + 6$	$=$	$0$

$\lim_{x \to - \infty} f (x)$	$=$	$\lim_{x \to - \infty} (e^{x^{2} - 2 x})$
	↓	Im Exponenten dominiert $" (- \infty)^{2} " = " + \infty "$
	$=$	$\lim_{x \to - \infty} (e^{" + \infty "})$
	↓	Verlauf der natürlichen Exponentialfunktion
	$=$	$+ \infty$

$\lim_{x \to + \infty} f (x)$	$=$	$\lim_{x \to + \infty} (e^{x^{2} - 2 x})$
	↓	Im Exponenten dominiert $" (+ \infty)^{2} " = " + \infty "$
	$=$	$\lim_{x \to - \infty} (e^{" + \infty "})$
	↓	Verlauf der natürlichen Exponentialfunktion
	$=$	$+ \infty$

Ableitungsfunktion bestimmen

Nullstellen der Ableitung

Art der Extremstelle

Lage der Extremstelle

Hast du eine Frage oder Feedback?

Nullstellen der zweiten Ableitung

Krümmungsverhalten

Stellen stärkster Zu- oder Abnahme

Hast du eine Frage oder Feedback?

Schnittpunkt mit der y-Achse

Schnittpunkte mit der x-Achse

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?