Stellen lokal stärkster Zu-&Abnahme

1
Der Graph $G_{f\ }$ hat bei $x=5$ eine Stelle lokal stärkster Zunahme. Welche Aussagen lassen sich über $G_{f'}$ und $G_{f''}$ an dieser Stelle definitiv treffen?
- $G_{f'}$ hat dort eine Nullstelle
- $G_{f'}$ hat dort einen Hochpunkt
- $G_{f'}$ hat dort einen Tiefpunkt
- $G_{f'}$ verläuft dort oberhalb der x-Achse
- $G_{f'}$ verläuft dort unterhalb der x-Achse
- $G_{f''}$ hat dort eine Nullstelle
- $G_{f''}$ hat dort eine Extremstelle
Die Stellen lokal stärkster Zu- oder Abnahme sind die Stellen, an denen die lokale Änderungsrate maximal oder minimal ist. Der Graph ist in der nahen Umgebung nirgendwo steiler (entweder steiler steigend oder steiler fallend).
Da die lokale Änderungsrate an einer Stelle $x_0$ dem Wert der Ableitung an dieser Stelle entspricht ( $f'\left(x_0\right)$ ), sind die Stellen lokal stärkster Zu- oder Abnahme genau die Extremstellen der Ableitung. Diese sind zugleich Nullstellen der zweiten Ableitung.
Der Graph steigt, wenn die lokale Änderungsrate, also der Wert der Ableitung an einer Stelle, positiv ist. Nur wenn der Graph steigt, kann überhaupt eine Stelle stärkster Zunahme vorliegen, denn sonst liegt ja gar keine Zunahme vor, sondern eine Abnahme. Deshalb muss $G_{f'}$ bei lokal stärkster Zunahme oberhalb der x-Achse verlaufen.
Zusammenfassend suchst du den Punkt von $G_{f'}$ , der oberhalb der x-Achse ist und in seiner direkten Umgebung am höchsten ist. Du suchst den lokalen Hochpunkt.
Kurzgesagt:
Stelle lokal stärkster Zunahme: Hochpunkt von $G_{f'}$ , der oberhalb von der x-Achse liegt.
Stellen stärkster Zunahme sind Hochpunkte von $G_{f'}$ , die oberhalb der x-Achse liegen müssen.
2
Entscheide, ob die Aussagen wahr oder falsch sind.
1. Hat der Graph $G_{f'}$ einer Ableitungsfunktion von f einen Tiefpunkt unterhalb der x-Achse, so hat der Graph $G_f$ dort eine Stelle lokal stärkster Abnahme.
  Wahr
  Falsch
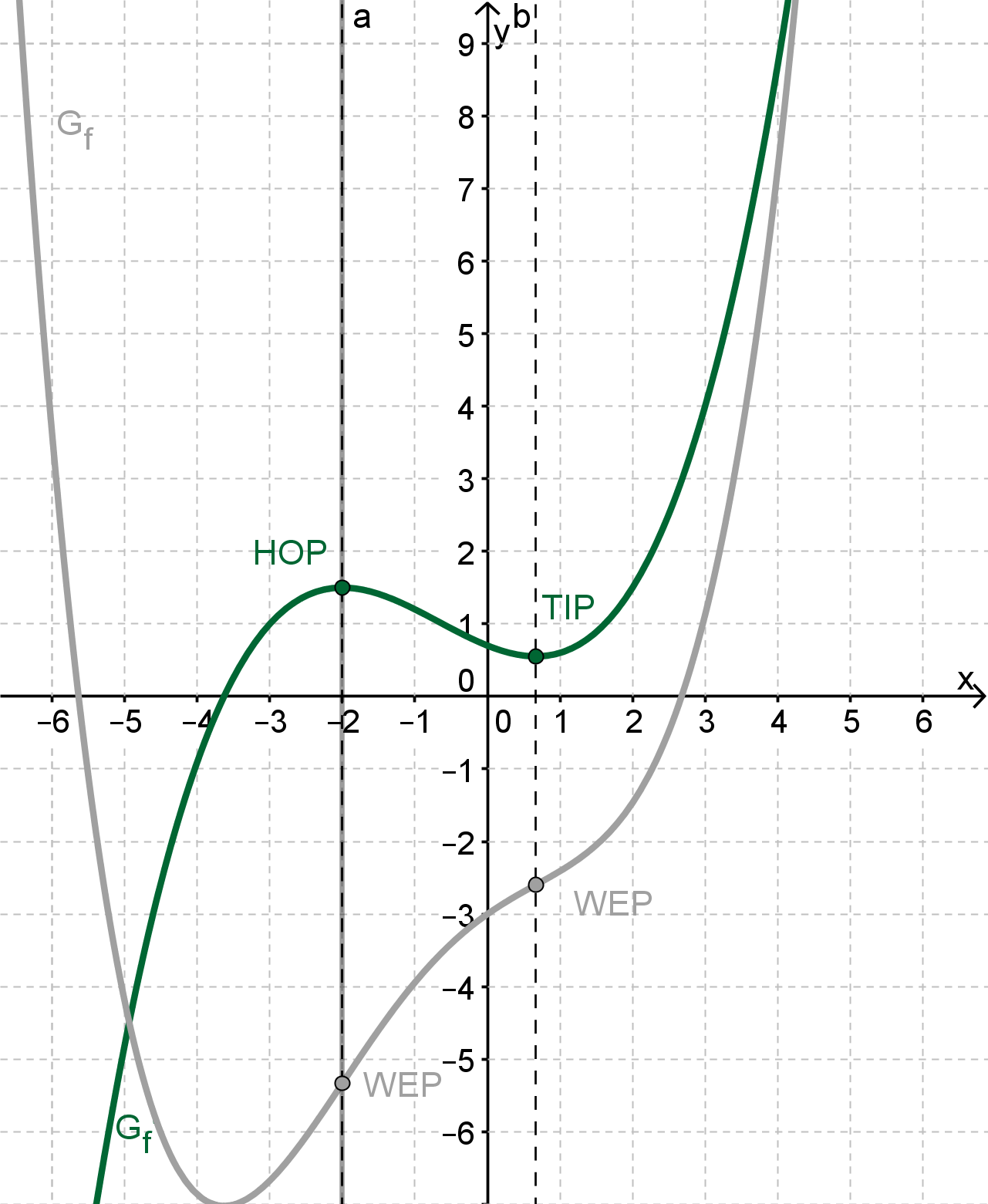
2. Hat der Graph von $G_{f'}$ einen Hochpunkt und einen Tiefpunkt, so hat der Graph $G_f$ einer Funktion f sowohl eine Stelle lokal stärkster Zunahme als auch lokal stärkster Abnahme
  Wahr
  Falsch
  
  Die Aussage ist falsch.
  Damit es eine Stelle lokal stärkster Abnahme gibt, muss der Tiefpunkt von $G_{f'}$ unterhalb der x-Achse liegen.
  Damit es eine Stelle lokal stärkster Zunahme gibt, muss der Hochpunkt von $G_{f'}$ oberhalb der x-Achse liegen.
  Gegenbeispiel:
  $G_{f'}$ hat einen Hochpunkt oberhalb der x-Achse und einen Tiefpunkt, der nicht unterhalb der x-Achse liegt.
  Ein möglicher Graph von f hat an beiden Extremstellen von f' einen Wendepunkt. Allerdings ist beim Hochpunkt von $G_{f'}$ der Wendepunkt von $G_f$ die Stelle lokal stärkster Zunahme, da der Graph dort offensichtlich am steilsten in der Umgebung ist und beim Tiefpunkt von $G_{f'}$ ist der Wendepunkt von $G_f$ eine Stelle lokal schwächster Zunahme, denn dort flacht der Graph von f ab, bevor er danach wieder steiler wird.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Wechselt der Graph einer Funktion f am Wendepunkt $W\left(x_w,\ y_w\right)$ von linksgekrümmt zu rechtsgekrümmt und es gilt $f'\left(x_W\right)>0$ , so hat der Graph dort eine Stelle lokal stärkster Zunahme.
  Wahr
  Falsch
4. Fällt der Graph von f an einem Wendepunkt, der zugleich kein Terrassenpunkt ist, so handelt es sich um eine Stelle stärkster Abnahme.
  Wahr
  Falsch
5. An einem Terrassenpunkt liegt immer eine Stelle lokal schwächster Zu- oder Abnahme vor.
  Wahr
  Falsch
3
Entscheiden Sie, ob die Aussagen wahr oder falsch sind.
1. Hat der Graph $G_{f'}$ einer Ableitungsfunktion von f einen Tiefpunkt unterhalb der x-Achse, so hat der Graph $G_f$ dort eine Stelle lokal stärkster Abnahme.
  Wahr
  Falsch
2. Hat der Graph von $G_{f'}$ einen Hochpunkt und einen Tiefpunkt, so hat der Graph $G_f$ einer Funktion f sowohl eine Stelle lokal stärkster Zunahme als auch lokal stärkster Abnahme
  Wahr
  Falsch
  
  Die Aussage ist falsch.
  Damit es eine Stelle lokal stärkster Abnahme gibt, muss der Tiefpunkt von $G_{f'}$ unterhalb der x-Achse liegen.
  Damit es eine Stelle lokal stärkster Zunahme gibt, muss der Hochpunkt von $G_{f'}$ oberhalb der x-Achse liegen.
  Gegenbeispiel:
  $G_{f'}$ hat einen Hochpunkt oberhalb der x-Achse und einen Tiefpunkt, der nicht unterhalb der x-Achse liegt.
  Ein möglicher Graph von f hat an beiden Extremstellen von f' einen Wendepunkt. Allerdings ist beim Hochpunkt von $G_{f'}$ der Wendepunkt von $G_f$ die Stelle lokal stärkster Zunahme, da der Graph dort offensichtlich am steilsten in der Umgebung ist und beim Tiefpunkt von $G_{f'}$ ist der Wendepunkt von $G_f$ eine Stelle lokal schwächster Zunahme, denn dort flacht der Graph von f ab, bevor er danach wieder steiler wird.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Wechselt der Graph einer Funktion f am Wendepunkt $W\left(x_w,\ y_w\right)$ von linksgekrümmt zu rechtsgekrümmt und es gilt $f'\left(x_W\right)>0$ , so hat der Graph dort eine Stelle lokal stärkster Zunahme.
  Wahr
  Falsch
4. Fällt der Graph von f an einem Wendepunkt, der zugleich kein Terrassenpunkt ist, so handelt es sich um eine Stelle stärkster Abnahme.
  Wahr
  Falsch
5. An einem Terrassenpunkt liegt immer eine Stelle lokal schwächster Zu- oder Abnahme vor.
  Wahr
  Falsch
4
Gegeben ist eine Funktion g mit $D=\mathbb{R}$ .
Beschreibe, wie du vorgehen musst, um die Stellen lokal stärkster Zu- bzw Abnahme zu bestimmen.
Kandidaten für Extremstellen der Ableitung suchen
Da an den Stellen lokal stärkster Zu-/Abnahme die lokale Änderungsrate extremal sein muss, werden die Extremstellen der Ableitung gesucht.
Dazu muss die Funktion g zweimal abgeleitet werden und die Nullstellen der zweiten Ableitung gefunden werden:
(Nebeneffekt: Die Stellen lokal stärkster Zu-/Abnahme sind immer Wendestellen der Funktion, aber nicht jede Wendestelle ist eine Stelle lokal stärkster Zu-/Abnahme)
Ergebnis: Es sind alle Kandidaten für Extremstellen von $G_{f'}$ bekannt.
Art der Extremstellen ermitteln
Insgesamt muss überprüft werden, ob die gefundenen Extrempunkte Hochpunkte oder Tiefpunkte sind, denn nur wenn ein Hochpunkt oberhalb der x-Achse oder ein Tiefpunkt unterhalb der x-Achse liegt, handelt es sich jeweils um eine Stelle lokal stärkster Zunahme oder lokal stärkster Abnahme (sonst: lokal schwächste Zu- oder Abnahme).
Die Art der Extremstelle kann z.B. ermittelt werden über:
Monotonietabelle für $G_{f'}$
Einsetzen der Extremstellen-Kandidaten in $G_{f'''}$ und Untersuchung des Vorzeichens
Beachte dabei, dass nicht wie gewohnt $G_f$ untersucht wird, sondern eben $G_{f'}$
Ergebnis: Du weißt, welche Extrempunkte Hochpunkte, Tiefpunkte oder Terrassenpunkte sind.
Wert der lokalen Änderungsrate bei Extremstellen ermitteln
Damit man bei einem Hochpunkt von einer stärksten Zunahme sprechen kann, muss überhaupt eine Zunahme vorliegen. Das bedeutet, dass die lokale Änderungsrate bzw Steigung positiv sein muss (analog bei Abnahme).
Deshalb wird die lokale Änderungsrate der gefundenen Stellen $x_1,x_2,...$ berechnet:
Zusammensetzen der Ergebnisse
Kombiniere nun die Ergebnisse aus dem 2. und 3. Schritt:
Hat der Graph der Ableitung einen Hochpunkt, der oberhalb der x-Achse liegt, so liegt eine Stelle lokal stärkster Zunahme vor
Hat der Graph der Ableitung einen Tiefpunkt, der unterhalb der x-Achse liegt, so liegt eine Stelle lokal stärkster Abnahme vor
Die Stellen lokal stärkster Zunahme sind die Hochpunkt von $G_{f'}$ , die oberhalb der x-Achse liegen und die Tiefpunkte von $G_{f'}$ , die unterhalb der x-Achse liegen.
Es müssen also drei Dinge überprüft werden:
Wo ist die Extremstelle von $G_{f'}$ ?
Was ist die Art der Extremstelle?
Liegt sie oberhalb oder unterhalb von der x-Achse?

Gegeben ist die Funktion f mit dem Graphen $G_f$ , der Definitionsmenge $D=\mathbb{R}$ und dem Funktionsterm $f\left(x\right)=0{,}2x^6-1{,}75x^4-6x^2$

Zeige, dass der Term der zweiten Ableitung $f''\left(x\right)=6x^4-21x^2-12$ ist.

$f\left(x\right)=0{,}2x^6-1{,}75x^4-6x^2$
$f'\left(x\right)=1{,}2x^5-7x^3-12x$
$f''\left(x\right)=6x^4-21x^2-12$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Leite mithilfe der Ableitungsregeln für Potenzfunktionen, für Faktoren und für Summen/Differenzen ab:
Treffe eine Aussage über die Symmetrie von $G_f$ , $G_{f'}$ und $G_{f''}$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrie von Graphen
Symmetrie von $G_f$
$f\left(x\right)=0{,}2x^6-1{,}75x^4-6x^2$
Da alle Potenzen gerade sind, ist $G_f$ symmetrisch zur y-Achse.
Symmetrie von $G_{f'}$
$f'\left(x\right)=1{,}2x^5-7x^3-12x$
Da alle Potenzen ungerade sind, ist $G_{f'}$ symmetrisch zum Ursprung.
Symmetrie von $G_{f''}$
$f''\left(x\right)=6x^4-21x^2-12$
Da alle Potenzen gerade sind, ist $G_{f''}$ symmetrisch zur y-Achse.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Für eine ganzrationale Polynomfunktion gilt:
Sind alle Potenzen von x gerade, so ist der zugehörige Graph achsensymmetrisch. Sind alle Potenzen von x ungerade, so ist der zugehörige Graph punktsymmetrisch.

Ermittle alle Stellen lokal stärkster Zu- oder Abnahme von $G_f$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Substitution

Nullstellen der 2. Ableitung

Die Kandidaten für Extremstellen der 1. Ableitung bekommst du, indem du die Nullstellen der 2. Ableitung bestimmst.

$\displaystyle f''\left(x\right)$	$=$	$\displaystyle 0$
$\displaystyle 6x^4-21x^2-12$	$=$	$\displaystyle 0$

Da es sich um eine biquadratische Gleichung handelt, kann mit $u=x^2$ substituiert werden:

$\displaystyle 6x^4-21x^2-12$	$=$	$\displaystyle 0$
$\displaystyle 6\left(x^2\right)^2-21x^2-12$	$=$	$\displaystyle 0$
	↓	Substituiere: $u=x^2$
$\displaystyle 6u^2-21u-12$	$=$	$\displaystyle 0$

Mithilfe der Mitternachtsformel kannst du die neue Gleichung lösen:

\displaystyle u_{1{,}2}=\frac{-\left(-21\right)\pm\sqrt{\left(-21\right)^2-4\cdot6\cdot\left(-12\right)}}{2\cdot6}

Es ergeben sich die Lösungen $u_1=4$ und $u_2=-0{,}5$

Vergiss nicht die Rücksubstitution. Für $u_1=4$ ergibt sich:

$\displaystyle u_1$	$=$	$\displaystyle 4$
	↓	Ersetze $u=x^2$
$\displaystyle x^2$	$=$	$\displaystyle 4$
	↓	Radiziere. Es gibt zwei Lösungen!
$\displaystyle x_1$	$=$	$\displaystyle 2$
$\displaystyle x_2$	$=$	$\displaystyle -2$

Das gleiche nochmal für $u_2=-0{,}5$

$\displaystyle u_2$	$=$	$\displaystyle -0{,}5$
	↓	Ersetze $u=x^2$
$\displaystyle x^2$	$=$	$\displaystyle -0{,}5$
	↓	Aus einer negativen Zahl kann keine Wurzel gezogen werden.

Keine weitere Lösung.

Art der Extremstelle

Mithilfe einer Monotonietabelle für $G_{f'}$ oder mithilfe der 3. Ableitung kann die Art der Extremstelle bestimmt werden. Hier ist die Lösung mithilfe der 3. Ableitung dargestellt:

$f'''\left(x\right)=24x^3-42x$

Setze $x_1=2$ und $x_2=-2$ jeweils in $f'''$ ein:

$f'''\left(2\right)=108>0$ , also Tiefpunkt von $G_{f'}$ bei $x=2$
$f'''\left(-2\right)=-108<0$ , also Hochpunkt von $G_{f'}$ bei $x=-2$

(Hinweis: Du könntest auch durch die Punktsymmetrie der 1. Ableitung direkt darauf schließen, dass das Verhalten bei $x=2_{ }$ gespiegelt auch für $x=-2$ gelten muss.)

Lage des Extrempunkts bzgl. der x-Achse

Damit es sich um eine Stelle lokal stärkster Abnahme handelt, müsste der Tiefpunkt von $G_{f'}$ bei $x=2$ unterhalb der x-Achse liegen. Setze den Wert in f' ein, um den Wert zu erhalten und zu entscheiden, ob für $G_f$ hier generell eine Zunahme oder Abnahme vorliegt.

$f'\left(2\right)=-41{,}6\ <0$ , also $G_{f'}$ hier unterhalb der x-Achse und somit eine Stelle lokal stärkster Abnahme.

Analog gilt für die Stelle stärkster Zunahme, dass der Hochpunkt von $G_{f'}$ bei $x=-2$ oberhalb von der x-Achse liegen muss.

$f'\left(-2\right)=41{,}6>0$ , also $G_{f'}$ hier oberhalb von der x-Achse und somit Stelle lokal stärkster Zunahme.

(Hinweis: Du könntest auch durch die Punktsymmetrie der 1. Ableitung direkt darauf schließen, dass das Verhalten bei $x=2_{ }$ gespiegelt auch für $x=-2$ gelten muss.)

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Begründe ohne weitere Rechnung, warum bei $x=0$ ein Tiefpunkt vorliegt und treffe eine Aussage über Art und ungefähre Lage weiterer Extrempunkte.

Extrempunkt bei x=0
Durch Faktorisieren erhält man den Term:
$f\left(x\right)=x^2\left(0{,}2x^4-1{,}75x^2-6\right)$
Da ein Produkt genau dann 0 ist, wenn eines seiner Faktoren 0 ist, hat die Funktion eine doppelte Nullstelle (Nullstelle mit Vielfachheit 2) bei x=0.
Eine doppelte Nullstelle berührt die x-Achse lediglich und ist deshalb automatisch auch eine Extremstelle.
Es steht noch aus, ob es sich um einen Tiefpunkt oder Hochpunkt handelt.
Weitere Extremstellen.
Da $G_f$ zwei Wendepunkte hat, die keine Terrassenpunkte sind ( $x=-2$ und $x=2$ ), muss der Graph 3 Extremstellen haben, da der Wendepunkt jeweils zwischen zwei Extremstellen liegen muss.
Es kann keine weiteren Extremstellen geben, da es keine weiteren Wendepunkte gibt und sich entweder vor oder nach einer Extremstelle (oder beide Male) die Krümmung ändern muss.
Es muss also ein weiterer Extempunkt in $]-\infty;-2[$ und einer in $]2;\infty[$ liegen. Aufgrund der Achsensymmetrie von $G_f$ sind beide Extrempunkte von der derselben Art.
Art aller drei Extremstellen
Da der Term vom Grad 4 ist und der Leitkoeffizient positiv ist, gilt
$\lim_{x\mapsto\pm\infty\ }f\left(x\right)=+\infty$ , was bedeutet, dass der Graph von f zu Beginn fällt. Der erste Extrempunkt im Intervall $]-\infty;-2[$ ist also ein Tiefpunkt.
Aufgrund der Symmetrie muss auch im Intervall $]2;\infty[$ ein Tiefpunkt sein.
Somit ist im Ursprung ein Hochpunkt.
(Hinweis: Die x-Koordinaten der anderen Extrempunkte können durch Faktorisieren der 1. Ableitung und durch Substitution berechnet werden. Sie liegen ungefähr bei $x_{E1}\approx -2{,}69$ und $x_{E2}\approx 2{,}69$ )
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Gegeben ist die Funktion f mit dem Graphen $G_f$ , der Definitionsmenge $D=\mathbb{R}$ und dem Funktionsterm $f\left(x\right)=2x^3+1{,}5x^2-2x+3$ .

Bestimme die Koordinaten der Punkte, an denen die lokale Änderungsrate den Wert 1 hat.

Untersuche, ob es eine Stelle lokal stärkster Zu- oder Abnahme gibt.

Untersuche den Graphen der Funktion f mit $f(x)=-\frac 1 3 x^3+3x^2-5x$ , $D_f=\R$ auf Stellen (lokal) stärkster Zu- oder Abnahme der Funktionswerte

Ableitung bestimmen

Bilde die 1. Ableitung der Funktion $f(x)=-\frac 1 3 x^3+3x^2-5x$ :

$f'(x)=x^2+6x-5$

Kandidaten für Extremstellen der 1. Ableitung suchen

Du suchst die Kandidaten für Extremstellen der 1. Ableitung (Achtung! Nicht von f selbst!).

Das sind die Stellen mit waagerechten Tangenten, also der Steigung 0.

Die 2. Ableitung beschreibt das Steigungsverhalten der 1. Ableitung:

$f''(x)=2x+6$

$\displaystyle f''\left(x\right)$	$=$	$\displaystyle 0$
$\displaystyle 2x+6$	$=$	$\displaystyle 0$	$\displaystyle -6$
$\displaystyle 2x$	$=$	$\displaystyle -6$
$\displaystyle x$	$=$	$\displaystyle -3$

Die Vielfachheit der Nullstelle $x=3$ ist 1, deshalb handelt es sich um eine Extremstelle von $f'$ (und nebenbei um eine Wendestelle von $f$ )

Art der Extremstelle

Die Art der Extremstelle kannst du zum Beispiel über eine Monotonietabelle bestimmen (alternativ über eine Skizze von $G_{f''}$ oder die 3. Ableitung).

	x<-3	x=-3	-3<x
Vorzeichen $f''$	-	0	+
Verlauf $G_{f'}$	$\searrow$	TIP	$\nearrow$

Der Graph der 1. Ableitung $G_{f'}$ hat nur eine Extremstelle. Einen Tiefpunkt bei $x=-3$

Lage des Extrempunkts

Du weißt nun, dass bei $x=-3$ ein Tiefpunkt liegt. Allerdings liegt hier nur eine Stelle lokal stärkster Abnahme vor, wenn der Graph $G_f$ tatsächlich zu diesem Zeitpunkt auch fällt. Das bedeutet, dass der Tiefpunkt von $G_{f'}$ unter der x-Achse liegen muss, also $f'(-3)<0$

$f'(-3)=(-3)^2+6\cdot(-3)-5=-14<0 \Rightarrow$ Der Graph $G_f$ fällt für $x=-3$ auch tatsächlich.

Folgerung lokal stärkste Abnahme

Da es sich beim Tiefpunkt $TIP(-3|-14)$ von $G_{f'}$ um einen Tiefpunkt unter der x-Achse handelt, hat der Graph $G_f$ dort zumindest eine Stelle lokal stärkster Abnahme.

Global stärkste Zu- oder Abnahme

Der Graph der Ableitung hat nur einen Extrempunkt, den gerade erwähnten Tiefpunkt. Der Graph der Ableitung ist also eine nach oben geöffnete Parabel.

Damit ist der Tiefpunkt der globale (absolute) Tiefpunkt der Ableitung und somit hat $G_f$ bei x=-3 eine Stelle global stärkster Abnahme.

Es gibt keinen (lokalen oder globalen) Hochpunkt bei $G_{f'}$ und deshalb auch keine Stelle global stärkster Zunahme bei $G_f$ .

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

(In Anlehnung an das Fachabitur T12 2022 in Bayern)

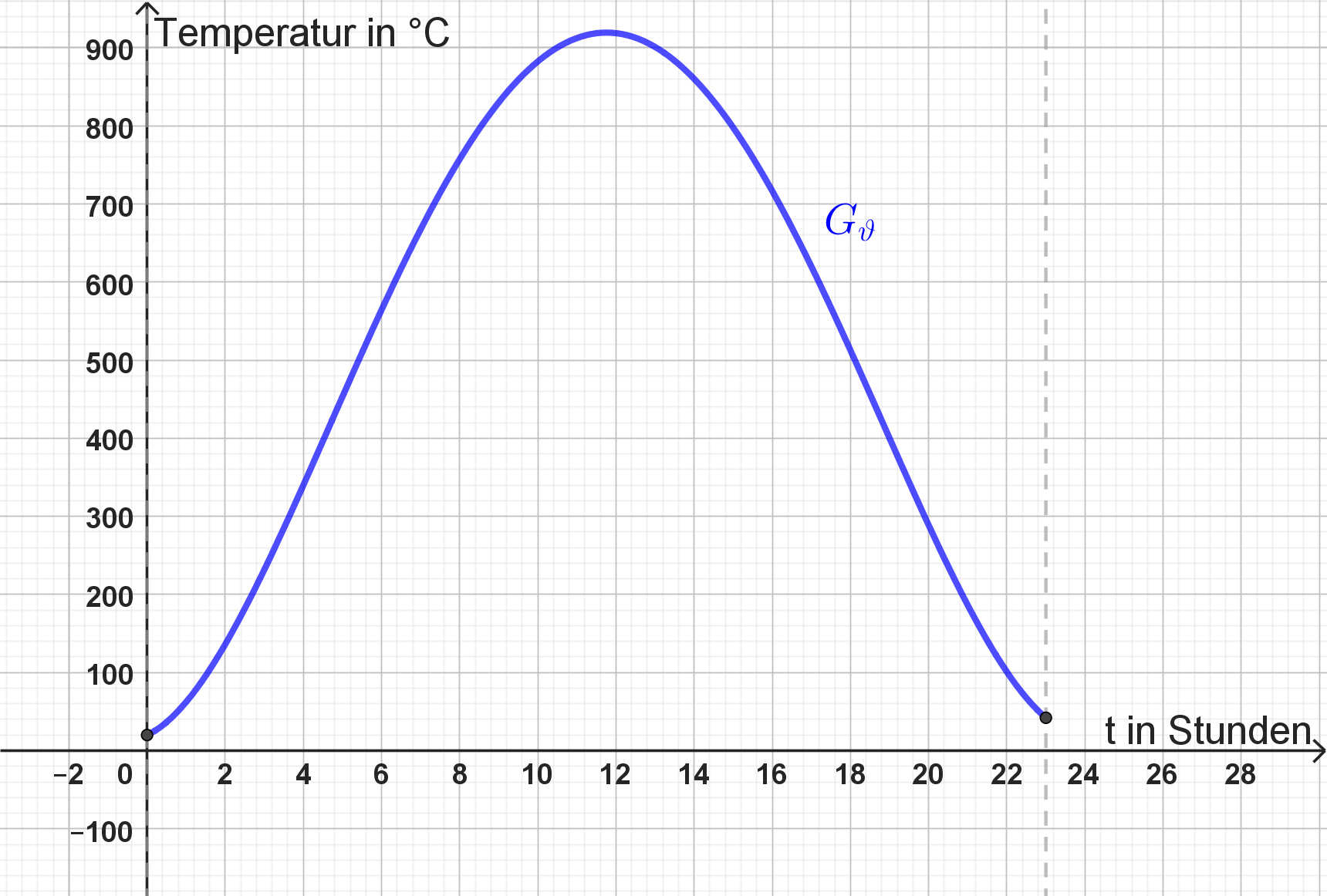
Das Brennen von Keramik erfolgt oft bei Temperaturen über 800°C. Die Temperatur im Ofen im Laufe des Brennvorgangs wird durch die sogenannte "Brennkurve" beschrieben. Die folgende Funktionsgleichung beschreibt in guter Näherung eine solche "Brennkurve" für einen Brennvorgang, der insgesamt 23 Stunden dauert:

$\vartheta(t)=0{,}04(t^4-47t^3+528t^2+576t+500)$ mit $D_{\vartheta}=[0;23]$

Die verstrichene Brenndauer t wird dabei in Stunden ab Beginn des Brennvorgangs zum Zeitpunkt $t=0$ angegeben, die Temperatur im Ofen $\vartheta(t)$ in Grad Celsius (°C).

Auf das Mitführen von Einheiten während der Berechnung kann verzichtet werden. Endergebnisse sind samt Einheit zu notieren. Zeitpunkte sind in Stunden auf zwei Nachkommastellen und Temperaturwerte in Grad Celsius ganzzahlig zu runden.

Bestimmen Sie den Zeitraum der Aufheizphase, in der die Temperatur im Brennofen ansteigt

1. Ableitung bestimmen

Bilde die erste Ableitung, mit der du das Steigungsverhalten (Monotonieverhalten) des Graphen beschreiben kannst:

$\vartheta(t)=0{,}04(t^4-47t^3+528t^2+576t+500)$

Ableiten:

$\vartheta'(t)=0{,}04(4t^3-141t^2+1056t+576)$

Nullstellen der 1. Ableitung bestimmen

Die Stellen, an denen sich das Monotonieverhalten ändern kann, sind die Stellen mit waagerechten Tangenten, also der Steigung 0. Deshalb suchst du die Nullstellen der Ableitung:

$\displaystyle \vartheta'(t)$	$=$	$\displaystyle 0$
$\displaystyle 0{,}04(4t^3-141t^2+1056t+576)$	$=$	$\displaystyle 0$
	↓	Satz vom Nullprodukt
$\displaystyle 4t^3-141t^2+1056t+576$	$=$	$\displaystyle 0$

Da der Grad der Funktion 3 ist und man nicht ausklammern kann, brauchst du die Polynomdivision.

Die erste Nullstelle musst du durch Probieren ermitteln. Eine Nullstelle findet man hier bei $x=24$ . Diese Nullstelle liegt zwar selbst nicht im Definitionsbereich $D=[0;23]$ , aber kann zur Polynomdivision trotzdem verwendet werden:

$\def\arraystretch{1.25} \begin{array}{lllll} &(4t^3&-141t^2&+1056t&+576) &:(t-24)=4t^2-45t-24\\ -&(4t^3&-96t^2)\\ &&-45t^2&+1056t\\ &-&(-45t^2&+1080t)\\ &&&\quad-24t&+576\\ &&-&(-24t&+576)\\ &&&&\quad0 \end{array}$

Nun kannst du die Mitternachtsformel verwenden:

$t_{2/3}=\frac{-(-45)\pm\sqrt{(-45^2)-4\cdot4\cdot(-24)}}{2\cdot 4}$ liefert $t_2\approx-0{,}51$ und $t_3\approx 11{,}76$

Nur die Nullstelle $t=11{,}76$ ist im Definitionsbereich und muss weiter betrachtet werden.

Monotonietabelle

Unter Verwendung von $D=[0;23]$ ergibt sich die Monotonietabelle

	0<x<11,76	x=11,76	11,76<x<23
Vorzeichen $\vartheta'$	+	0	-
Verlauf $G_{\vartheta}$	$\nearrow$ sms	HOP	$\searrow smf$

Die Aufheizphase dauert vom Messbeginn an ca 12 Stunden (genauer 11,76 Stunden).

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Damit das Brenngut keinen Schaden nimmt, darf während der Aufheizphase die momentane Änderungsrate der Temperatur höchstens 115°C pro Stunde betragen. Untersuchen Sie, ob diese Bedingung erfüllt wird.

Bei Temperaturen im Ofen von 1400°C und mehr müssen besonders hitzebeständige Tragegestelle für die Keramikteile verwendet werden. Entscheiden Sie mithilfe einer Rechnung, ob ein besonders hitzebeständiges Tragegestell verwendet werden muss.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Art und Lage von Extrempunkten
Bei $t=11{,}76$ hat der Graph $G_\vartheta$ seinen Hochpunkt und somit der Ofen seine maximale Temperatur.
Diese beträgt $\vartheta(11{,}76)\approx 919°C$ und ist somit unter der Temperatur von 1400°C.
Es wird also kein spezielles Tragegeschirr benötigt.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Hier geht es wieder um die tatsächliche Temperatur zu einem bestimmten Zeitpunkt und nicht um die Temperaturzunahme.
Mithilfe der Ergebnisse aus der ersten Teilaufgabe kann man schnell überprüfen, ob die Maximaltemperatur 14000°C übersteigt, indem man die Lage des Extrempunktes bestimmt.
Zeichnen Sie den Graphen von $\vartheta$ für $0\leq t\leq 23$ in ein kartesisches Koordinatensystem. Maßstab: t-Achse: 2 Stunden $\hat{=}$ 1 cm und $\vartheta$ (t)-Achse: 100°C $\hat{=}$ 1 cm.

Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Achte auf den Definitionsbereich und halte die Grenzen ein.
Außerdem ist eine besondere Achsenskalierung vorhanden.
Den Hochpunkt solltest du aus deinen bereits bestimmten Ergebnissen ebenfalls einzeichnen.

9
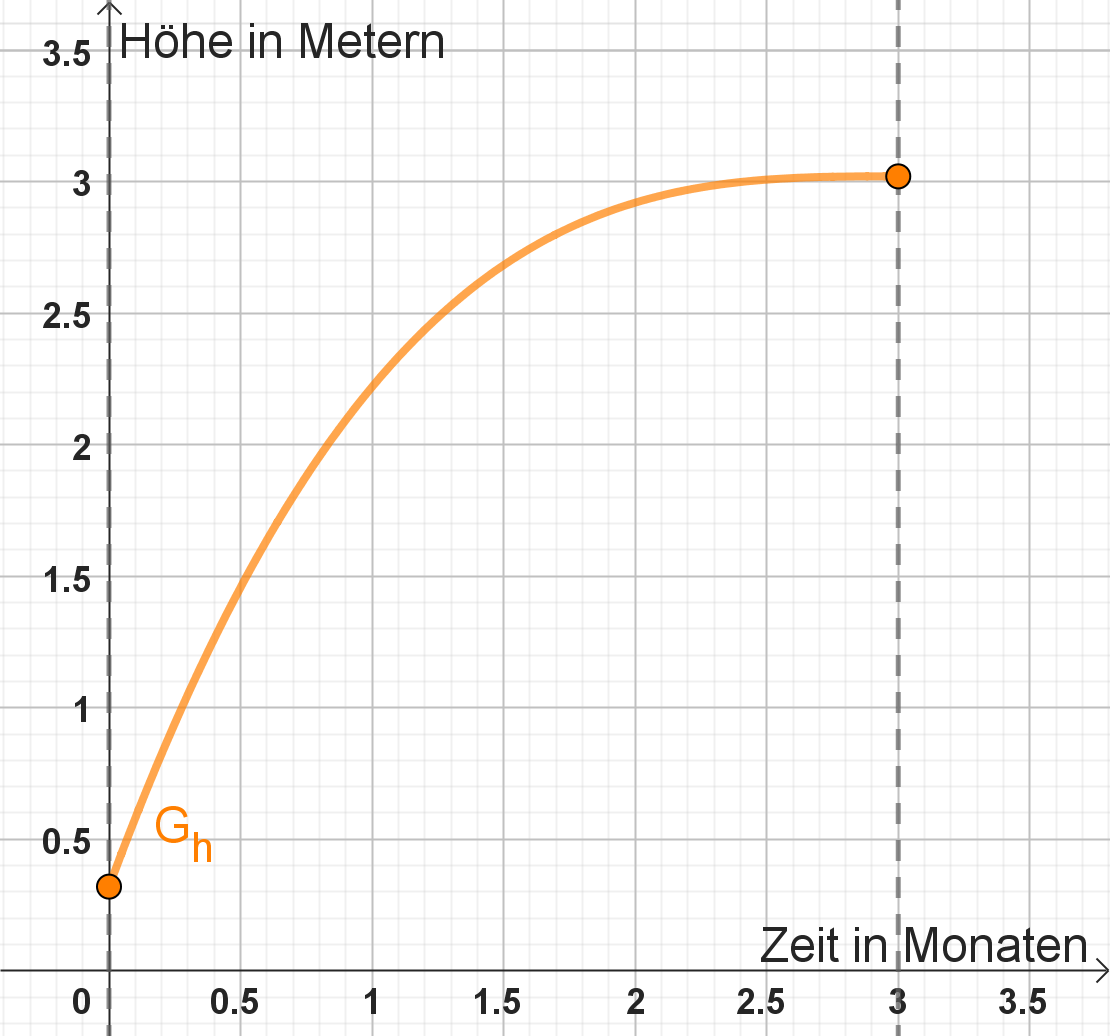
Eine Sonnenblume wird gepflanzt und monatlich ihre Höhe in Metern gemessen. Dabei wird als erste Messung (Zeitpunkt 0. Monat) die Höhe der Sonnenblume vier Wochen nach dem Einpflanzen betrachtet, damit das Pflänzchen bereits gut sichtbar ist. Die Funktion $h(m)=\frac 1 {50}(5m^3-45m^2+135m+16)$ kann im Zeitraum $D=[0;3]$ zur Beschreibung der Situation herangezogen werden.
1. Gib die Bedeutung von $h(m)$ und $m$ im Sachkontext an
  
  Die Größe m beschreibt die Zeit in Monaten ab der 1. Messung - gemein, da m zugleich die Einheit von $h(m)$ ist, der Höhe der Sonnenblume in Metern.
  Später in der Aufgabe häufig noch wichtig: Der Zeitpunkt $m=0$ ist nicht der Zeitpunkt des Einpflanzens. Es wurde erst gemessen, als die Pflanze gut sichtbar war: 4 Wochen nach dem Einpflanzen.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Lies den Text aufmerksam durch.
  Was ist die unabhängige Größe, die auf der x-Achse zu finden ist?
  Was ist die abhängige Größe, also was wird in Abhängigkeit von etwas anderem angegeben?
2. Bestimme h(0) und erkläre die Bedeutung des Wertes im Sachzusammenhang
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionswerte
  $h(0)=\frac 1{50}(5\cdot 0^3-45\cdot0^2+135\cdot0+16)=0{,}32$
  Hierbei handelt es sich um die Höhe der Sonnenblume bei der Startmessung (vier Wochen nach dem Einpflanzen). Die Blume ist also 32 cm hoch.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne den Funktionswert bei $m=0$
  Die erste Teilaufgabe hilft dir dabei, herauszufinden, für was $m$ und für was $h(m)$ steht.
3. Bestimme die Höhe der Sonnenblume 10 Wochen nach Aussaat.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionswert
  Ziehe zunächst die 4 Wochen bis zur ersten Messung ab: $10-4=6$
  Vom Zeitpunkt $m=0$ sind es also noch 6 Wochen oder 1,5 Monate (1 Monat $\approx$ 4 Wochen).
  $h(1{,}5)\approx 2{,}68$
  Zehn Wochen nach der Aussaat ist die Sonnenblume ungefähr 2,68 m hoch.
  (Ja, Sonnenblumen werden tatsächlich bis zu 3 m groß, brauchen dafür eigentlich aber ungefähr doppelt so lang...)
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Vergiss nicht, dass Aussaat und Messstart zwei unterschiedliche Dinge sind.
  Wenn du die Wochen in Monate umgerechnet hast, kannst du erneut den Funktionswert bestimmen.
4. Zeichne den Graphen von h in ein geeignetes Koordinatensystem. Beschrifte die Achsen sprechend.
  
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5. Bestimme das durchschnittliche Wachstum der Sonnenblume im ersten Monat der Messungen.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Differenzenquotient
  Setze in die Formel des Differenzenquotienten ein, um eine durchschnittliche Steigung zu bestimmen:
  $m=\frac{h(1)-h(0)}{1-0}=\frac{2{,}22-0{,}32}1=1{,}9$
  Im ersten Monat wächst sie durchschnittlich mit einer Geschwindigkeit von $1{,}9$ Meter pro Monat.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme die durchschnittliche Steigung mit der mittleren Änderungsrate (dem Differenzenquotient)
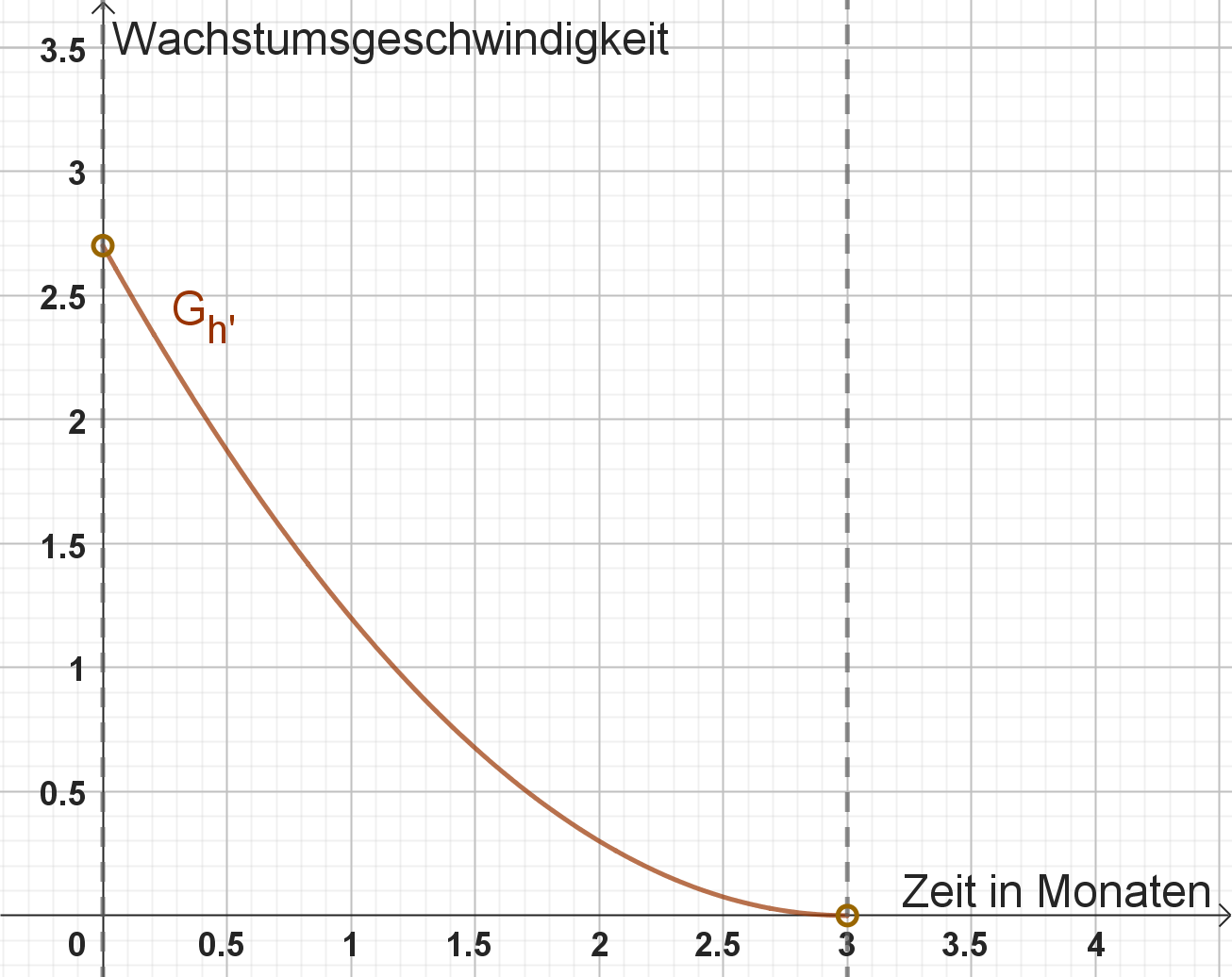
6. Erkläre die Bedeutung der Ableitung $h'(m)$ im Sachkontext.
  
  In dieser Aufgabe ist die Ableitung die Wachstumsgeschwindigkeit der Sonnenblume in Meter pro Monat ( $\frac{\text{Meter}}{\text{Monat}}$ )
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Die Einheit der Ableitung ist die Einheit der y-Achse dividiert durch die Einheit der x-Achse.
  Die Ableitung gibt immer eine Änderungsrate an.
7. Zeichne den Graphen von $h'$ in ein neues Koordinatensystem. Verwende erneut sprechende Achsenbeschriftungen.
  
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle f'\left(x\right)$	$=$	$\displaystyle 1$
$\displaystyle 6x^2+3x-2$	$=$	$\displaystyle 1$	$\displaystyle -1$
$\displaystyle 6x^2+3x-3$	$=$	$\displaystyle 0$

$\displaystyle f''(x)$	$=$	$\displaystyle 0$
$\displaystyle 12x+3$	$=$	$\displaystyle 0$	$\displaystyle -3$
$\displaystyle 12x$	$=$	$\displaystyle -3$	$\displaystyle :12$
$\displaystyle x$	$=$	$\displaystyle -\frac 1 4$

$\displaystyle \vartheta''\left(t\right)$	$=$	$\displaystyle 0$
$\displaystyle 0{,}04\left(12t^2-282t+1056\right)$	$=$	$\displaystyle 0$
	↓	Satz vom Nullprodukt
$\displaystyle 12t^2-282t+1056$	$=$	$\displaystyle 0$

Stellen lokal stärkster Zu-&Abnahme

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Kandidaten für Extremstellen der Ableitung suchen

Art der Extremstellen ermitteln

Wert der lokalen Änderungsrate bei Extremstellen ermitteln

Zusammensetzen der Ergebnisse

Hast du eine Frage oder Feedback?

Symmetrie von GfG_fGf​

Symmetrie von Gf′G_{f'}Gf′​

Symmetrie von Gf′′G_{f''}Gf′′​

Hast du eine Frage oder Feedback?

Nullstellen der 2. Ableitung

Art der Extremstelle

Lage des Extrempunkts bzgl. der x-Achse

Hast du eine Frage oder Feedback?

Extrempunkt bei x=0

Weitere Extremstellen.

Art aller drei Extremstellen

Hast du eine Frage oder Feedback?

Ableiten

Gleichung lösen

Koordinaten

Hast du eine Frage oder Feedback?

Ableiten

Nullstellen der 2. Ableitung

Art der Extremstelle über 3. Ableitung

Lage des Tiefpunkts

Hast du eine Frage oder Feedback?

Ableitung bestimmen

Kandidaten für Extremstellen der 1. Ableitung suchen

Art der Extremstelle

Lage des Extrempunkts

Folgerung lokal stärkste Abnahme

Global stärkste Zu- oder Abnahme

1. Ableitung bestimmen

Nullstellen der 1. Ableitung bestimmen

Monotonietabelle

Hast du eine Frage oder Feedback?

2. Ableitung bilden

Nullstellen der 2. Ableitung bestimmen

Lage der Extremstellen von Gf′G_{f'}Gf′​

Fazit

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Symmetrie von $G_f$

Symmetrie von $G_{f'}$

Symmetrie von $G_{f''}$

Lage der Extremstellen von $G_{f'}$