Der Hauptunterschied zwischen einem bestimmten und einem unbestimmten Integral ist das Vorhandensein (bestimmtes Integral) bzw. Fehlen (unbestimmtes Integral) der Integrationsgrenzen.
Ein bestimmtes Integral beschreibt einen orientierten Flächeninhalt, ist also ein einfacher Zahlenwert.
Ein unbestimmtes Integral ist die Menge aller sogenannten Stammfunktionen.
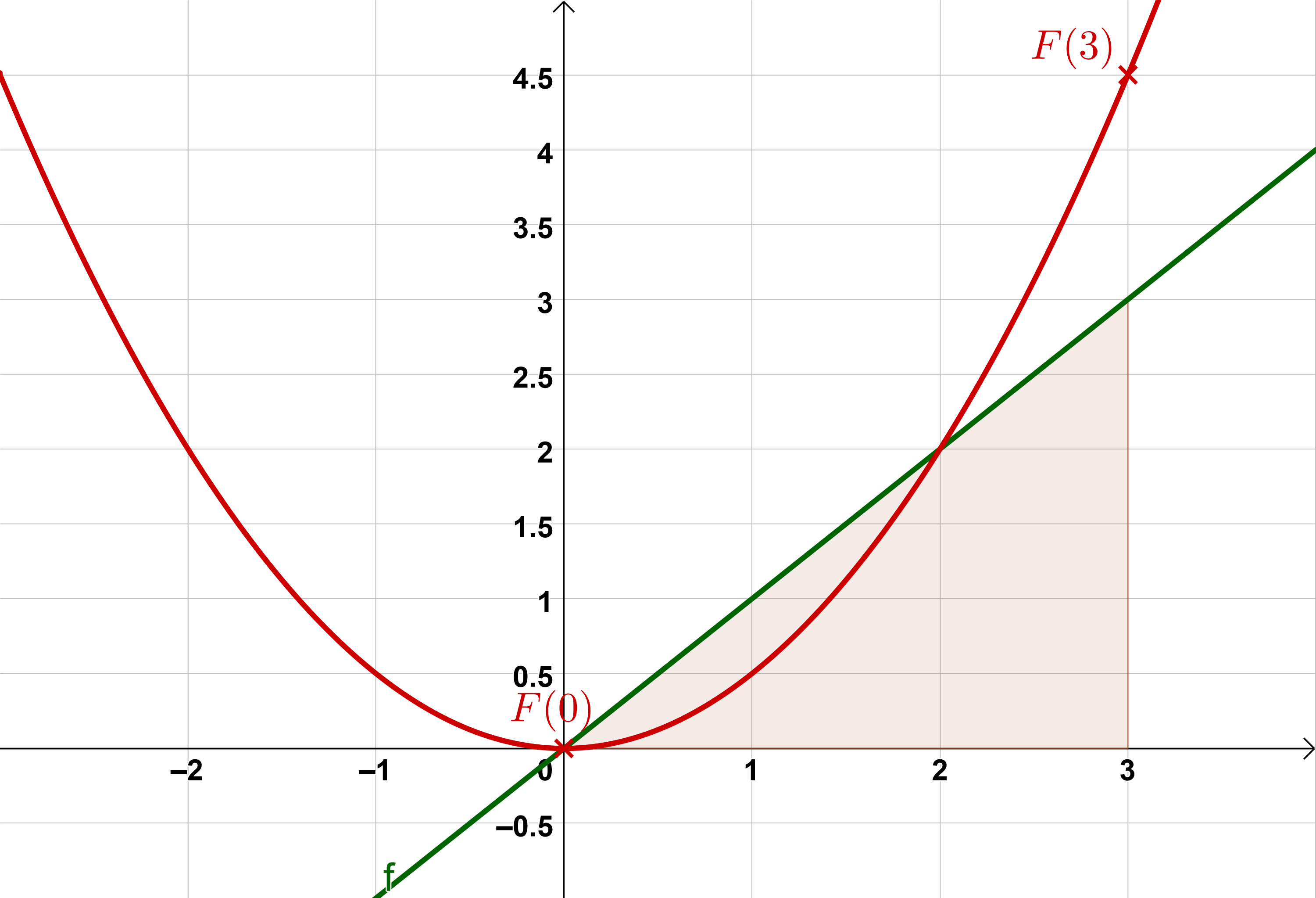
Bestimmtes Integral der Funktion in den Grenzen a=0 und b=3.
Bestimmte Integrale
Man berechnet den Wert des Integrals mit dem Hauptsatz der Differential- und Integralrechnung:
,
wobei eine Stammfunktion von ist.
Das Ergebnis ist ein konkreter Zahlenwert. Das Ergebnis ist damit eindeutig.
Unbestimmte Integrale
Unbestimmte Integrale haben keine Integralgrenzen.
Sie zu berechnen bedeutet, eine Stammfunktion der Funktion im Integral (dem sogenannten Integranden) zu finden. Diese ist jedoch nur bis auf eine Konstante eindeutig: Da eine Stammfunktion abgeleitet wieder die Funktion ergeben muss, kann eine beliebige konstante Zahl zu einer Stammfunktion addiert werden und die neue Funktion ist immer noch eine Stammfunktion, da Konstanten beim Ableiten verschwinden.
Eine Funktion hat also immer unendlich viele Stammfunktionen. Man verdeutlicht dies, indem man hinter eine allgemeine Stammfunktion den Term ergänzt, wobei die sogenannte Integrationskonstante C für eine beliebige Zahl aus steht:
für eine allgemeine Stammfunktion mit .
Vom unbestimmten zum bestimmten Integral
Wenn ein bestimmtes Integral gesucht ist, können wir zunächst das unbestimmte Integral bestimmen und durch die Wahl eines konkreten das bestimmte Integral ermitteln.
Beispiel
Man berechne .
Das unbestimmte Integral ist gegeben durch .
Mit dem Hauptsatz der Differential- und Integralrechnung gilt nun:
.
Hier sieht man, dass die konkrete Wahl der additiven Konstanten keinen Einfluss auf den Wert des bestimmten Integrals hat.
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
