Lineares Wachstum bzw. linearer Zerfall liegt dann vor, wenn die Änderung eines Wertes , bei gleicher zeitlicher Änderung, konstant ist.
Anders gesagt: Die Ausgangsmenge verändert sich in gleichen Zeitabständen um die immer gleiche Menge. Die lineare Wachstumsfunktion ist eine Geradengleichung:
Dabei ist:
: die Anzahl bzw. Größe von nach der Zeit ,
: die Änderungsrate,
: die Anzahl bzw. Größe von nach der Zeit , also der Startwert.
Eigenschaften
Die Wachstumsgeschwindigkeit bzw. Änderungsrate ist bei linearem Wachstum bzw. Zerfall konstant: .
Sie entspricht der Steigung des Graphen der linearen Wachstumsfunktion.
Monotonie: Ist , spricht man von linearem Wachstum. Die Funktion ist dann streng monoton steigend.
Ist , beschreibt die Funktion linearen Zerfall. Die Funktion ist dann streng monoton fallend.
Der Graph einer linearen Wachstumsfunktion
Wie bei linearen Funktionen wird die Änderungsrate mit Hilfe eines Steigungsdreiecks berechnet.
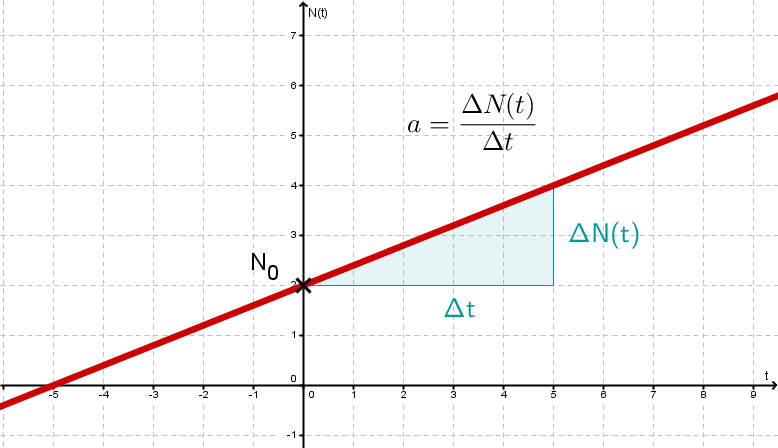
bezeichnet die Differenz der Werte von zu zwei Zeitpunkten.
Im Graphen links:
steht für die Zeitspanne, in der man beobachtet. Hier:
Beispiel
Ein Baum wird in den Garten gepflanzt. Zu diesem Zeitpunkt ragt er um aus dem Boden heraus. Nach wie vielen Jahren ist der Baum hoch, wenn er durchschnittlich im Jahr um wächst?
Lösung:
Als Erstes schreibt man sich die gegebenen und gesuchten Werte aus der Angabe heraus.
Gesucht ist der Zeitpunkt , zu dem der Baum die Größe erreicht hat.
Gegeben ist die Größe des Baumes zu Beginn (= Startwert ), seine Wachstumsgeschwindigkeit (= Änderungsrate ) und seine nach Jahren erreichte Größe (= )
(Bemerkung: wird in Jahren angegeben, gibt die Größe des Baumes in Meter an.
Der Baum wächst pro Jahr, daher ist die Einheit von .)
Nun setzt man die gegebenen Werte in die Funktionsgleichung ein und löst die Gleichung nach dem gesuchten auf.
Antwort: Nach Jahren ist der Baum hoch.
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
