In diesem Artikel werden mehrere Vorgehensweisen beschrieben, mit deren Hilfe sich quadratische Funktionen mit gegebenen Eigenschaften (wie z. B. Punkte, die der Graph durchlaufen soll) aufstellen lassen.
Es werden Aufgabentypen erklärt:
Punkte gegeben
Scheitel und ein weiterer Punkt gegeben
Punkte und Zusatzinformationen gegeben
Parabel als Graph der Funktion gegeben
3 Punkte gegeben
Da eine quadratische Funktion in ihrer Normalform durch eindeutig bestimmt ist, bekommt man nach Einsetzen von drei Punkten ein lineares Gleichungssystem mit drei Gleichungen und den drei gesuchten Werten , und , das man lösen muss.
Allgemeine Vorgehensweise für 3 gegebene Punkte
1. Schritt | Gegebene Punktepaare in die Funktionsgleichung einsetzen, sodass man drei Gleichungen erhält. |
|---|---|
2. Schritt | |
3. Schritt | Funktionsterm angeben. |
Beispielaufgabe
Gesucht ist die quadratische Funktion, die die Punkte , und durchläuft.
1. Schritt: Gegebene Punktepaare in die Funktionsgleichung einsetzen.
2. Schritt: Gleichungssystem lösen
Wie man ein Gleichungssystem löst, erfährst du im Artikel Additionsverfahren.
Ausführliche Rechnung, hier mit Additionsverfahren
Zuerst solltest du die Zahlen auf der rechten Seite ausmultiplizieren.
Du stellst fest, dass alle drei Gleichungen den Term am Ende haben. Du kannst diesen also loswerden, indem du eine Gleichung von einer anderen subtrahierst. Indem du zum Beispiel von subtrahierst, erhältst du:
Diese Gleichung lässt sich ganz leicht nach auflösen. Es gilt:
, oder einfach
Auch wenn du die Gleichung von der Gleichung subtrahierst, verschwindet . Dann erhältst du:
Setzt du hier die Auflösung von oben ein, erhältst du:
,
und die Gleichung lässt sich zusammenfassen zu
Addierst du auf beiden Seiten, so erhältst du
Durch auf beiden Seiten teilen liefert:
Da schon bekannt war, kannst du hier einsetzen und so ist
Nun kannst du beide Werte von und in einsetzen und erhältst:
| ↓ | Vereinfachen | ||
Als Ergebnis bekommt man also .
3. Schritt: Funktionsterm angeben: .
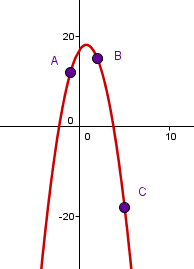
Scheitel und ein weiterer Punkt gegeben
Hat man einen Scheitelpunkt und einen weiteren Punkt gegeben, so empfiehlt es sich, die Scheitelform aufzustellen und anschließend den fehlenden Parameter mithilfe des gegebenen Punktes auszurechnen. Um die Funktion in der Form zu erhalten, muss man nun noch ausmultiplizieren.
Allgemeine Vorgehensweise für gegebenen Scheitel und gegebenem Punkt
1. Schritt | Scheitelpunkt verwenden, um die Scheitelform aufzustellen |
|---|---|
2. Schritt: | Den noch fehlenden Parameter berechnen, indem man den gegebenen Punkt in die Scheitelform einsetzt und nach dem Parameter auflöst. |
3. Schritt: | Funktionsterm angeben. |
Tipp
Der Scheitelpunkt kann auch indirekt gegeben sein, indem man ihn mit Verschiebungen beschreibt. "Die Parabel ist um nach rechts und nach oben verschoben" bedeutet zum Beispiel, dass der Scheitelpunkt bei liegt.
Beispielaufgabe
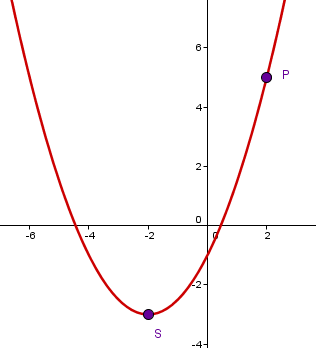
Gesucht ist die quadratische Funktion mit dem Scheitel , die durch den Punkt verläuft.
1. Schritt: Scheitelpunkt S verwenden, um die Scheitelform aufzustellen: .
2. Schritt: Den noch fehlenden Parameter berechnen, indem man den gegebenen Punkt P in die Scheitelform einsetzt und nach auflöst:
3. Schritt:
Die quadratische Funktion lautet somit oder ausmultipliziert .
Punkte und Zusatzinformationen gegeben
Oftmals sind in der Aufgabenstellung noch zusätzliche Informationen gegeben, mit deren Hilfe man dann die Funktionsvorschrift angeben kann. Oft reicht aber eine Zusatzinformation nicht aus, da sie wenig verwertbare Informationen liefert.
Beispiele für Zusatzinformationen
"Normalparabel": Der Vorfaktor ist gleich (wenn die Parabel nach oben geöffnet ist) oder gleich (Parabel nach unten geöffnet).
"nach oben geöffnete Parabel" bzw. "nach unten geöffnete Parabel": Positives bzw. negatives Vorzeichen des Vorfaktors (siehe Parabel )
"nimmt nur positive / negative Werte an": Parabel verläuft immer über / unter der -Achse. -Koordinate des Scheitels größer/kleiner .
"selbe -Koordinate bei den Punkten": Der Scheitel liegt bezüglich der x-Koordinate genau zwischen den beiden Punkten (Symmetrie von Parabeln).
"doppelte Nullstelle": Hat eine Parabel eine doppelte Nullstelle, dann ist diese der Scheitelpunkt. Er liegt also auf der -Achse und besitzt somit die -Koordinate .
Beispielaufgabe
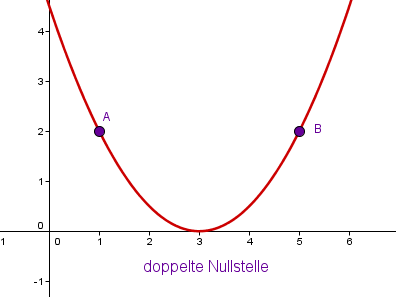
Gesucht ist eine Parabel, die eine doppelte Nullstelle hat und durch die Punkte und geht.
In diesem Fall lautet die Zusatzinformation "doppelte Nullstelle". Das heißt, der Scheitel liegt auf der x-Achse. Zusätzlich haben die beiden Punkte dieselbe y-Koordinate, d. h., der Scheitel liegt genau dazwischen. Zusammen ergibt sich für den Scheitel .
Jetzt kann man mit den drei Punkten ein lineares Gleichungssystem lösen oder mit dem Scheitel die Scheitelform aufstellen und einen anderen Punkt einsetzen. Man erhält also zuerst und setzt z. B. den Punkt ein, um zu erhalten. Insgesamt ergibt sich
Parabel als Funktionsgraph gegeben
Falls die Parabel als Funktionsgraph im Koordinatensystem gegeben ist, kann man die Funktionsgleichung auf zwei Arten ablesen:
Drei Punkte ablesen
Man kann günstig gelegene Punkte aus dem Koordinatensystem ablesen, um die bekannten Lösungsansätze anzuwenden. Praktische Punkte sind dabei der Scheitelpunkt und die Nullstellen.
Direkt ablesen
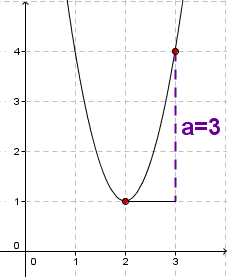
Man kann die Gleichung auch direkt ablesen. Dazu benutzt man den Scheitelform .
Die Koeffizienten und sind die Koordinaten des Scheitelpunkts
Der Koeffizient lässt sich ablesen, indem man vom Scheitelpunkt aus eine Einheit nach rechts oder links geht und abliest, wie weit man nach oben (falls positiv ist) oder nach unten (falls negativ ist) gehen muss.
Beispiel
Der Scheitelpunkt liegt bei , also bekommt man
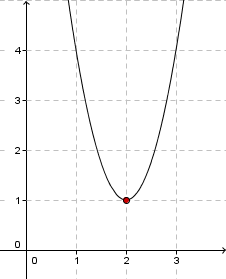
Geht man vom Scheitelpunkt aus um eine Einheit nach rechts, so muss man drei Schritte nach oben gehen, bis man wieder auf dem Graphen ist. Also ist der Funktionsterm