Gegeben sind die Funktionsgleichungen folgender Parabeln.
Bestimme jeweils die Scheitelform und den Scheitelpunkt.
Berechne die Achsenschnittpunkte.
Beschreibe schrittweise, wie aus der Normalparabel durch Verschieben/Strecken entsteht und wie sie geöffnet ist.
Zeichne den Graphen von in ein geeignetes Koordinatensystem.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Funktionen
Scheitelpunkt berechnen
↓ In die Scheitelform umwandeln. Dazu die quadratische Ergänzung machen.
↓ Umformen in eine Binomische Formel.
Achsenschnittpunkte berechnen
Schnittpunkte mit der x-Achse
↓ Nullstelle berechnen. Die Gleichung gleich 0 setzen.
↓ Mitternachtsformel anwenden. Dazu zuerst die Diskriminante D berechnen.
2 Lösungen:
Schnittpunkt mit der y-Achse
Für x gleich 0 setzen.
Verschiebung
Normalparabel:
Die verschiedenen Verschiebungen lassen sich an der Scheitelform ablesen:
Verschiebung um 2 LE nach rechts.
Verschiebung um 2 LE nach unten.
Zeichnung
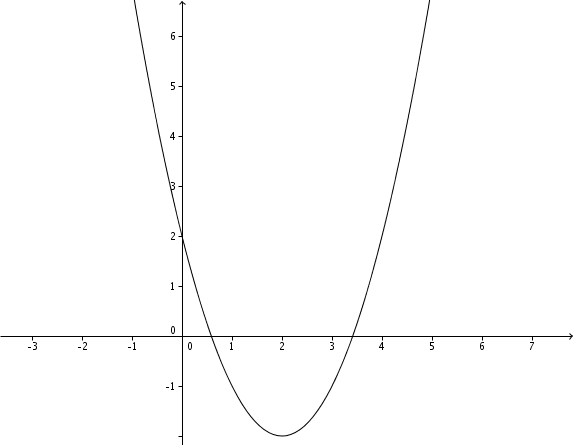
Hast du eine Frage oder Feedback?
Führe eine quadratische Ergänzung durch, um von der Normalform in die Scheitelform zu gelangen. Dort kann der Scheitel, sowie die Verschiebungen der Parabel direkt aus dem Funktionsterm entnommen werden.
Verwende die Informationen aus den Teilaufgaben 1, 2 und 3, um Punkte (beispielsweise der Scheitelpunkt) der Parabel in ein Koordinatensystem zu skizzieren. Verbinde diese Punkte mit einer Kurve, die keine Ecken oder Sprünge aufweist.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Funktionen
Scheitelpunkt berechnen
↓ In die Scheitelform umwandeln. Dazu die quadratische Ergänzung machen.
↓ Umformen in eine Binomische Formel.
Achsenschnittpunkte berechnen
Schnittpunkte mit der x-Achse
↓ Nullstelle berechnen . Die Gleichung gleich 0 setzen.
↓ Mitternachtsformel anwenden. Dazu zuerst die Diskriminante D berechnen.
2 Lösungen
Schnittpunkt mit der y-Achse
Für x gleich 0 setzen.
Verschiebung des Funktionsgraphen
Normalparabel:
Die verschiedenen Verschiebungen lassen sich an der Scheitelform ablesen.
Verschiebung um 2 LE nach links.
Verschiebung um 2 LE nach unten.
Zeichnung
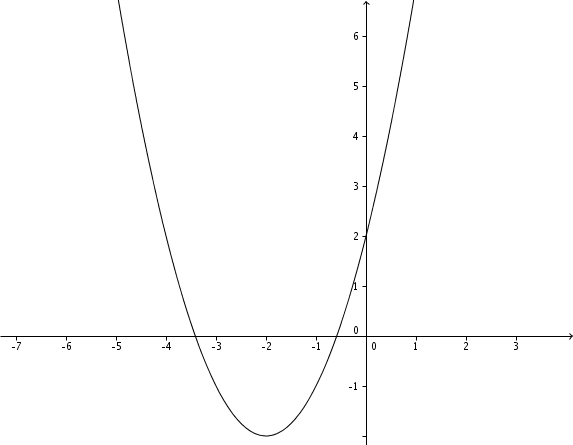
Hast du eine Frage oder Feedback?
Führe eine quadratische Ergänzung durch, um von der Normalform in die Scheitelform zu gelangen. Dort kann der Scheitel, sowie die Verschiebungen der Parabel direkt aus dem Funktionsterm entnommen werden.
Verwende die Informationen aus den Teilaufgaben 1, 2 und 3, um Punkte (beispielsweise der Scheitelpunkt) der Parabel in ein Koordinatensystem zu skizzieren. Verbinde diese Punkte mit einer Kurve, die keine Ecken oder Sprünge aufweist.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Funktionen
Scheitelpunkt berechnen
↓ Minus ausklammern. Distributivgesetz.
↓ In die Scheitelform umwandeln. Dazu die quadratische Ergänzung machen.
↓ Umformen in eine Binomische Formel.
Achsenschnittpunkte berechnen
Schnittpunkte mit der x-Achse
↓ Nullstelle berechnen. Die Gleichung gleich 0 setzen.
↓ Mitternachtsformel anwenden. Dazu zuerst die Diskriminante D berechnen.
2 Lösungen
Schnittpunkt mit der y-Achse
Für x gleich 0 setzen.
Verschiebung des Funktionsgraphen
Normalparabel:
Die verschiedenen Verschiebunge n lassen sich an der Scheitelform ablesen.
Nach unten geöffnet.
Verschiebung um 2 LE nach links.
Verschiebung um 7 LE nach oben.
Zeichnung
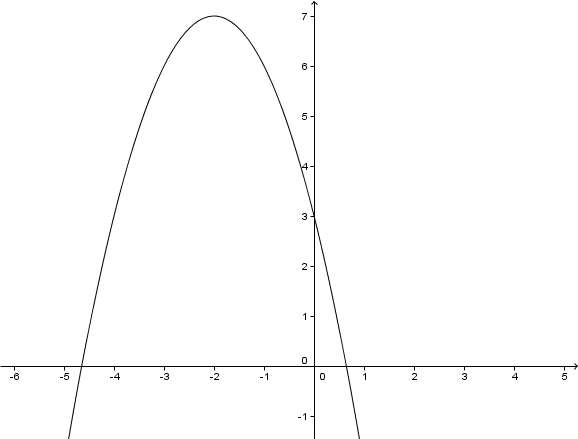
Hast du eine Frage oder Feedback?
Führe eine quadratische Ergänzung durch, um von der Normalform in die Scheitelform zu gelangen. Dort kann der Scheitel, sowie die Verschiebungen der Parabel direkt aus dem Funktionsterm entnommen werden.
Verwende die Informationen aus den Teilaufgaben 1, 2 und 3, um Punkte (beispielsweise der Scheitelpunkt) der Parabel in ein Koordinatensystem zu skizzieren. Verbinde diese Punkte mit einer Kurve, die keine Ecken oder Sprünge aufweist.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Funktionen
Scheitelpunkt berechnen
↓ Minus ausklammern. Distributivgesetz.
↓ In die Scheitelform umwandeln. Dazu die quadratische Ergänzung machen.
↓ Umformen in eine Binomische Formel.
↓ Distributivgesetz anwenden.
Achsenschnittpunkte berechnen
Schnittpunkte mit der x-Achse
↓ Nullstelle berechnen. Die Gleichung gleich 0 setzen.
↓ Mitternachtsformel anwenden. Dazu zuerst die Diskriminante D berechnen.
2 Lösungen
Schnittpunkt mit der y-Achse
Für x gleich 0 setzen.
Verschiebung des Funktionsgraphen
Normalparabel:
Die verschiedenen Verschiebungen lassen sich an der Scheitelform ablesen.
Nach unten geöffnet.
Verschiebung um 4 LE nach rechts.
Verschiebung um 7 LE nach oben.
Zeichnung
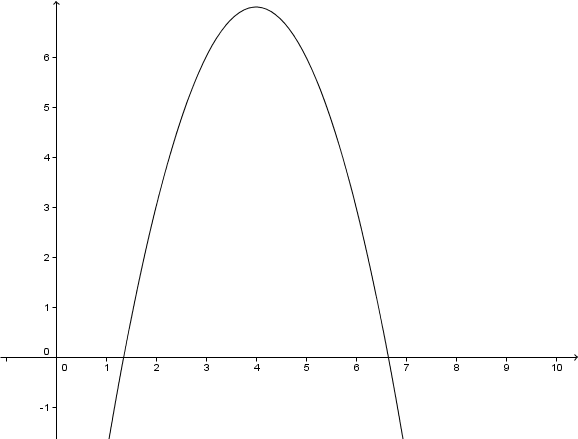
Hast du eine Frage oder Feedback?
Führe eine quadratische Ergänzung durch, um von der Normalform in die Scheitelform zu gelangen. Dort kann der Scheitel, sowie die Verschiebungen der Parabel direkt aus dem Funktionsterm entnommen werden.
Verwende die Informationen aus den Teilaufgaben 1, 2 und 3, um Punkte (beispielsweise der Scheitelpunkt) der Parabel in ein Koordinatensystem zu skizzieren. Verbinde diese Punkte mit einer Kurve, die keine Ecken oder Sprünge aufweist.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Funktionen
Scheitelpunkt berechnen
↓ ausklammern. Distributivgesetz .
↓ In die Scheitelform umwandeln. Dazu die quadratische Ergänzung machen.
↓ Umformen in eine Binomische Formel .
↓ Distributivgesetz anwenden.
Achsenschnittpunkte berechnen
Schnittpunkte mit der x-Achse
↓ Nullstelle berechnen. Die Gleichung gleich 0 setzen.
↓ Mitternachtsformel anwenden. Dazu zuerst die Diskriminante D berechnen.
2 Lösungen
Schnittpunkt mit der y-Achse
Für x gleich 0 setzen.
Verschiebung des Funktionsgraphen
Normalparabel:
Die verschiedenen Verschiebungen lassen sich an der Scheitelform ablesen.
Gestaucht durch den Faktor .
Verschiebung um 4 LE nach rechts.
Verschiebung um 3 LE nach unten.
Zeichnung
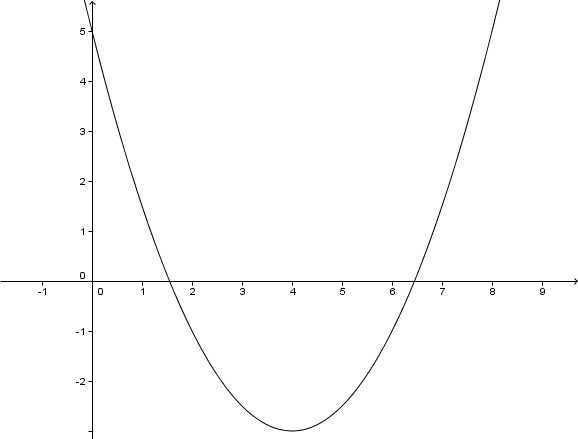
Hast du eine Frage oder Feedback?
Führe eine quadratische Ergänzung durch, um von der Normalform in die Scheitelform zu gelangen. Dort kann der Scheitel, sowie die Verschiebungen der Parabel direkt aus dem Funktionsterm entnommen werden.
Verwende die Informationen aus den Teilaufgaben 1, 2 und 3, um Punkte (beispielsweise der Scheitelpunkt) der Parabel in ein Koordinatensystem zu skizzieren. Verbinde diese Punkte mit einer Kurve, die keine Ecken oder Sprünge aufweist.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Funktionen
Scheitelpunkt berechnen
↓ ausklammern. Distributivgesetz .
↓ In die Scheitelform umwandeln. Dazu die quadratische Ergänzung machen.
↓ Umformen in eine Binomische Formel.
↓ Distributivgesetz anwenden.
Achsenschnittpunkte berechnen
Schnittpunkte mit der x-Achse
↓ Nullstelle berechnen. Die Gleichung gleich 0 setzen.
↓ ausklammern. Distributivgesetz .
↓ Satz von Vieta anwenden.
;
Schnittpunkt mit der y-Achse
Für x gleich 0 setzen.
Verschiebung des Funktionsgraphen
Normalparabel:
Die verschiedenen Verschiebungen lassen sich an der Scheitelform ablesen.
Nach unten geöffnet.
Gestaucht durch den Faktor .
Verschiebung um 2 LE nach links.
Verschiebung um 8 LE nach oben.
Zeichnung
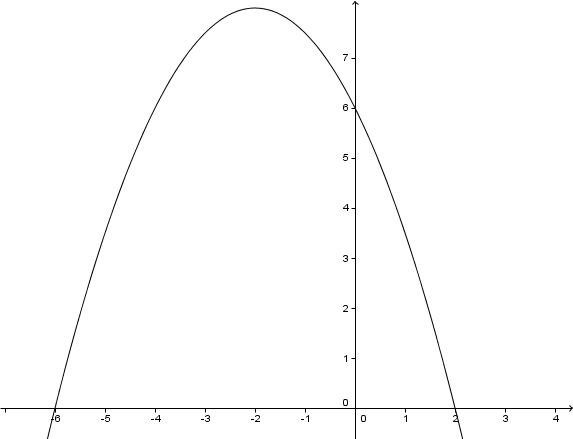
Hast du eine Frage oder Feedback?
Führe eine quadratische Ergänzung durch, um von der Normalform in die Scheitelform zu gelangen. Dort kann der Scheitel, sowie die Verschiebungen der Parabel direkt aus dem Funktionsterm entnommen werden.
Verwende die Informationen aus den Teilaufgaben 1, 2 und 3, um Punkte (beispielsweise der Scheitelpunkt) der Parabel in ein Koordinatensystem zu skizzieren. Verbinde diese Punkte mit einer Kurve, die keine Ecken oder Sprünge aufweist.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Funktionen
Scheitelpunkt berechnen
↓ ausklammern. Distributivgesetz.
↓ In die Scheitelform umwandeln. Dazu die quadratische Ergänzung machen.
↓ Umformen in eine Binomische Formel.
↓ Distributivgesetz anwenden.
Achsenschnittpunkte berechnen
Schnittpunkte mit der x-Achse
↓ Nullstelle berechnen . Die Gleichung gleich 0 setzen.
↓ Mitternachtsformel anwenden. Dazu zuerst die Diskriminante D berechnen.
2 Lösungen
Schnittpunkt mit der y-Achse
Für x gleich 0 setzen.
Verschiebung des Funktionsgraphen
Normalparabel:
Die verschiedenen Verschiebungen lassen sich an der Scheitelform ablesen.
Gestaucht durch den Faktor .
Verschiebung um 1 LE nach rechts.
Verschiebung um LE nach unten.
Zeichnung
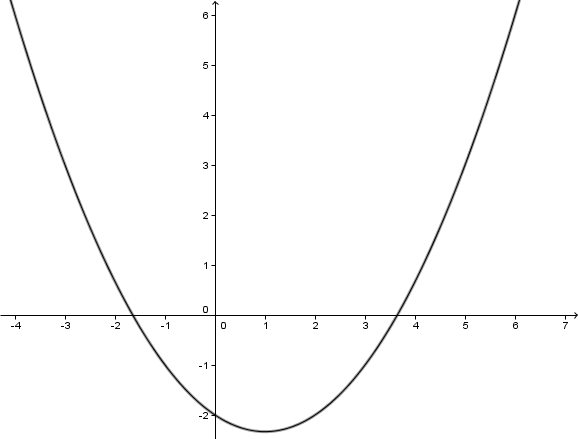
Hast du eine Frage oder Feedback?
Führe eine quadratische Ergänzung durch, um von der Normalform in die Scheitelform zu gelangen. Dort kann der Scheitel, sowie die Verschiebungen der Parabel direkt aus dem Funktionsterm entnommen werden.
Verwende die Informationen aus den Teilaufgaben 1, 2 und 3, um Punkte (beispielsweise der Scheitelpunkt) der Parabel in ein Koordinatensystem zu skizzieren. Verbinde diese Punkte mit einer Kurve, die keine Ecken oder Sprünge aufweist.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Funktionen
Scheitelpunkt berechnen
↓ ausklammern. Distributivgesetz.
↓ Vereinfachen
↓ In die Scheitelform umwandeln. Dazu die quadratische Ergänzung machen.
↓ Distributivgesetz anwenden.
↓ Vereinfachen
Achsenschnittpunkte berechnen
Schnittpunkte mit der x-Achse
↓ Nullstelle berechnen. Die Gleichung gleich 0 setzen.
↓ Mitternachtsformel anwenden. Dazu zuerst die Diskriminante D berechnen.
2 Lösungen
Schnittpunkt mit der y-Achse
x gleich 0 setzen.
Verschiebung des Funktionsgraphen
Normalparabel:
Die verschiedenen Verschiebungen lassen sich an der Scheitelform ablesen.
Nach unten geöffnet.
Gestaucht durch den Faktor .
Verschiebung um LE nach rechts.
Verschiebung um LE nach oben.
Zeichnung
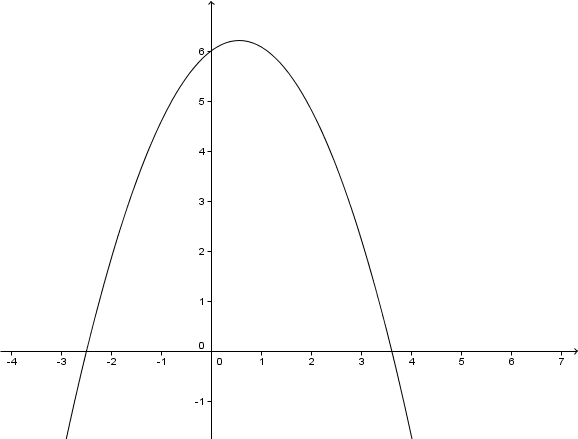
Hast du eine Frage oder Feedback?
Führe eine quadratische Ergänzung durch, um von der Normalform in die Scheitelform zu gelangen. Dort kann der Scheitel, sowie die Verschiebungen der Parabel direkt aus dem Funktionsterm entnommen werden.
Verwende die Informationen aus den Teilaufgaben 1, 2 und 3, um Punkte (beispielsweise der Scheitelpunkt) der Parabel in ein Koordinatensystem zu skizzieren. Verbinde diese Punkte mit einer Kurve, die keine Ecken oder Sprünge aufweist.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
