Lineare Abhängigkeit bzw. Unabhängigkeit sind Begriffe aus der Vektorgeometrie.
Zwei oder mehr Vektoren sind dann linear abhängig, wenn sich der Nullvektor durch eine Linearkombination der Vektoren bilden lässt.
Definition
Zwei Vektoren
sind linear abhängig, wenn sie kollinear, d.h. parallel verlaufen:
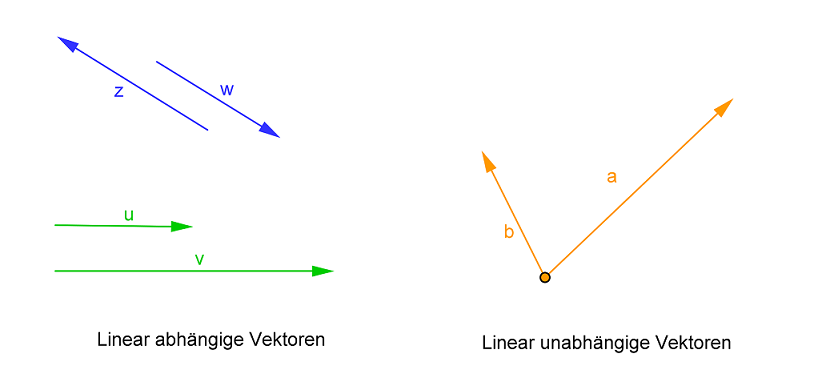
Drei Vektoren
sind linear abhängig, wenn sie komplanar, d.h. in einer Ebene sind und man mit ihnen eine geschlossene Vektorkette bilden kann.
Gilt dies nicht, sind die Vektoren linear unabhängig.
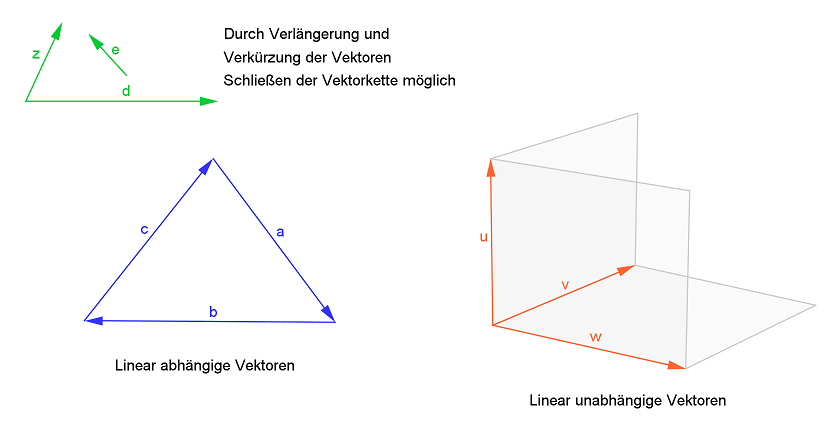
Insbesondere folgt daraus bereits, dass drei Vektoren im immer linear abhängig sind, da sie sich alle in einer Ebene befinden.
Allgemeine Definition
Eine Menge von Vektoren ist linear abhängig, wenn man eine Linearkombination von ihnen bilden kann, die den Nullvektor ergibt und nicht trivial ist (trivial wäre, einfach von allen Vektoren das Nullfache zu nehmen).
Geht das nicht, so sind sie linear unabhängig.
Berechnung bei zwei Vektoren
Zwei Vektoren und sind dann linear abhängig, wenn einer ein Vielfaches des anderen ist: mit .
Beispiel 1
Die zwei Vektoren und sind linear abhängig, da .
Beispiel 2
Die zwei Vektoren und sind linear unabhängig. Wären sie linear abhängig, so könnte man ausdrücken als . Das ist nicht möglich, da die erste Komponente der Vektoren impliziert - das passt aber nicht zur zweiten Komponente, da .
Beispiel 3
Die zwei Vektoren und sind linear abhängig, da .
Beispiel 4
Die zwei Vektoren und sind linear unabhängig. Wären sie linear abhängig, so könnte man ausdrücken als . Das ist nicht möglich, da die erste und zweite Komponente der Vektoren impliziert, das aber nicht zur dritten Komponente passt - schließlich gilt .
Berechnung bei drei Vektoren
Drei Vektoren sind dann linear abhängig, wenn sich eine geschlossene Vektorkette bilden lässt. Dabei dürfen allerdings nicht alle k-Parameter gleich null sein.
Formel zur Überprüfung
Beispiel 1
Die drei Vektoren , und sind linear abhängig, da z. B. gilt.
Beispiel 2
Die drei Vektoren , und sind linear unabhängig, da sie sich nicht in einer Ebene befinden.
Beispiel 3
Die drei Vektoren , und sind linear abhängig, da z. B. gilt.
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zur linearen Unabhängigkeit
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
