Das Skalarprodukt ist eine Multiplikation von zwei Vektoren. Sein Ergebnis ist ein Skalar (= eine reelle Zahl), im Gegensatz zum Kreuzprodukt, dessen Ergebnis ein Vektor ist.
Für das Skalarprodukt der Vektoren und schreibt man , oder auch .
Anmerkung: Um das Skalarprodukt (Vektor mal Vektor) vom skalaren Multiplizieren (Zahl mal Vektor) zu unterscheiden, verwenden wir hier als Symbol für das Skalarprodukt.
Wichtig: Man kann das Skalarprodukt von zwei Vektoren nur bilden, wenn sie beide gleich viele Komponenten haben.
Definition
Das Skalarprodukt von zwei Vektoren und ist definiert als
ihre komponentenweise Multiplikation und die
anschließende Addition.
Dies bedeutet:
In der Ebene
Im Raum
In beiden Fällen wird
die von mit der von ,
die von mit der von
und im Raum auch
die von mit der von
multipliziert. Diese Produkte werden dann addiert.
Beispiel
Berechne das Skalarprodukt zwischen den beiden Vektoren und !
Wende die Definition an und du erhältst:
Das Skalarprodukt von und beträgt somit .
Verwendung des Skalarproduktes
Senkrechte Vektoren
Zwei Vektoren stehen senkrecht bzw. orthogonal zueinander, genau dann, wenn ihr Skalarprodukt ergibt. Du hast also
Beispiel
Überprüfe, ob die Vektoren und senkrecht aufeinander stehen!
Berechne das Skalarprodukt der beiden Vektoren:
Da ihr Skalarprodukt ist, stehen die beiden Vektoren senkrecht aufeinander.
Länge eines Vektors
Die Länge eines Vektors (der Betrag) ist gleich der Wurzel aus dem Skalarprodukt des Vektors mit sich selbst:
In der Ebene
Im Raum
Beachte, dass lediglich der Nullvektor die Länge hat.
Beispiel
Berechne die Länge des Vektors .
Bestimme zunächst das Skalarprodukt von mit sich selbst:
Ziehst du nun die Wurzel aus diesem Skalarprodukt, so erhältst du die Länge des Vektors .
Der Vektor besitzt also die Länge .
Winkel zwischen Vektoren
Mit dem Skalarprodukt lässt sich der Winkel ermitteln, den zwei Vektoren miteinander einschließen (vorausgesetzt, keiner von ihnen ist der Nullvektor). Der Winkel hat immer einen Wert zwischen 0 und bzw. zwischen und .
Für den Winkel zwischen zwei Vektoren und gilt:
Durch Umformen erhältst du:
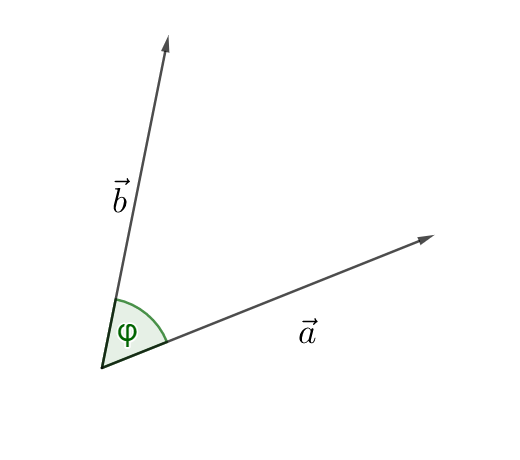
Wichtig: In dieser Formel sind die Längen von und im Nenner. Daher muss man darauf achten, dass weder noch gleich dem Nullvektor sind.
Beispiel
Berechne den Winkel, der zwischen den beiden Vektoren und eingeschlossen wird!
Berechne zuerst das Skalarprodukt:
.
Als Nächstes berechnest du jeweils die Länge der beiden Vektoren:
Einsetzen des Skalarprodukts und der Länge der Vektoren in die Formel für den Winkel liefert:
Der Winkel zwischen den beiden Vektoren und ist also .
Übungsaufgaben
Laden
Laden
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
