Das Vektorprodukt ist die Verknüpfung zweier Vektoren, dessen Ergebnis wieder ein Vektor ist, der senkrecht auf den beiden Vektoren steht.
Häufig wird das Vektorprodukt auch mit "Kreuzprodukt" bezeichnet.
Mathematisch ist das Kreuzprodukt zweier Vektoren und definiert als
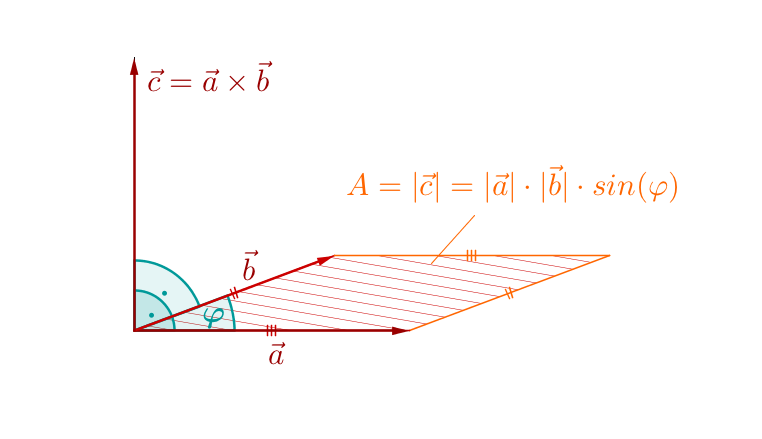
Der dadurch erhaltene Vektor steht auf und senkrecht ( und ).
Er hat die Länge , wobei der Winkel ist, den und aufspannen. Der Wert entspricht dem Flächeninhalt des von und aufgespannten Parallelogramms.
Beispiel
Für und ist das Kreuzprodukt
Wir können eine erste Probe dadurch machen, dass das Kreuzprodukt auf den Faktoren senkrecht stehen muss, das Skalarprodukt muss also Null sein:
Schema zum Berechnen
Um nicht die ganze Formel auswendig lernen zu müssen, gibt es folgenden Trick:
1) Man schreibt die oberen zwei Zeilen noch einmal unter die Vektoren:
2) Anschließend fängt man bei der 2. und 3. Zeile an und verrechnet zwei Zeilen immer folgendermaßen:
() ().
Dies ist dann die erste Zeile des neuen Vektors.
Wir rechnen , also
3) Damit haben wir den ersten Eintrag des Kreuzprodukts gefunden. Den zweiten finden wir mit demselben Verfahren aus den dritten und vierten Zeilen der Vektoren:
Wir rechnen , also
4) Für den dritten Eintrag des Kreuzprodukts machen wir dasselbe mit den vierten und fünften Zeilen der Vektoren:
Wir rechnen , also
Damit haben wir das Kreuzprodukt berechnet.
Eigenschaften
Das Kreuzprodukt ist weder assoziativ noch kommutativ!
Jedoch gelten folgende Gesetze:
(Distributivgesetze)
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Vektorprodukt
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
