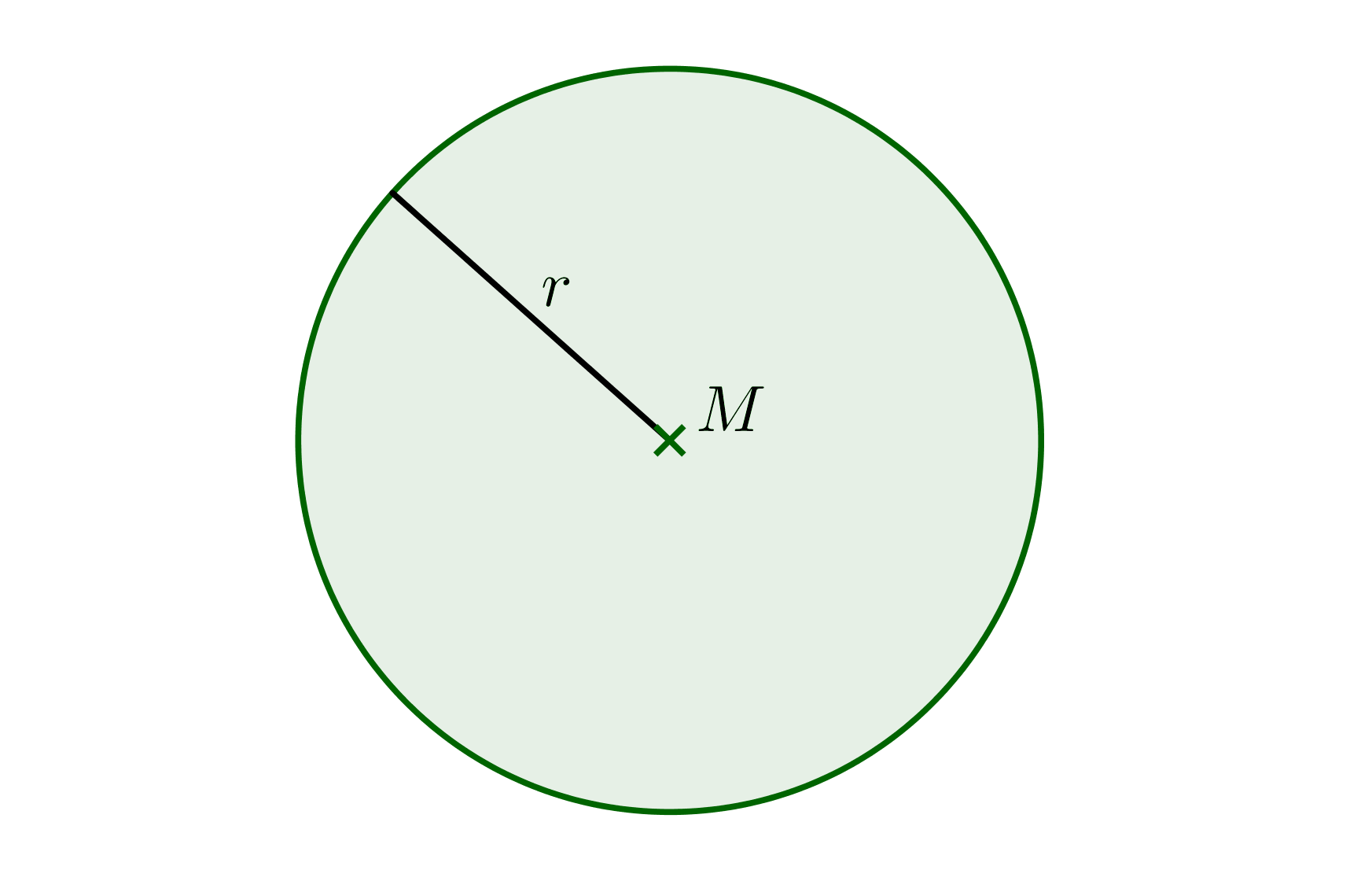
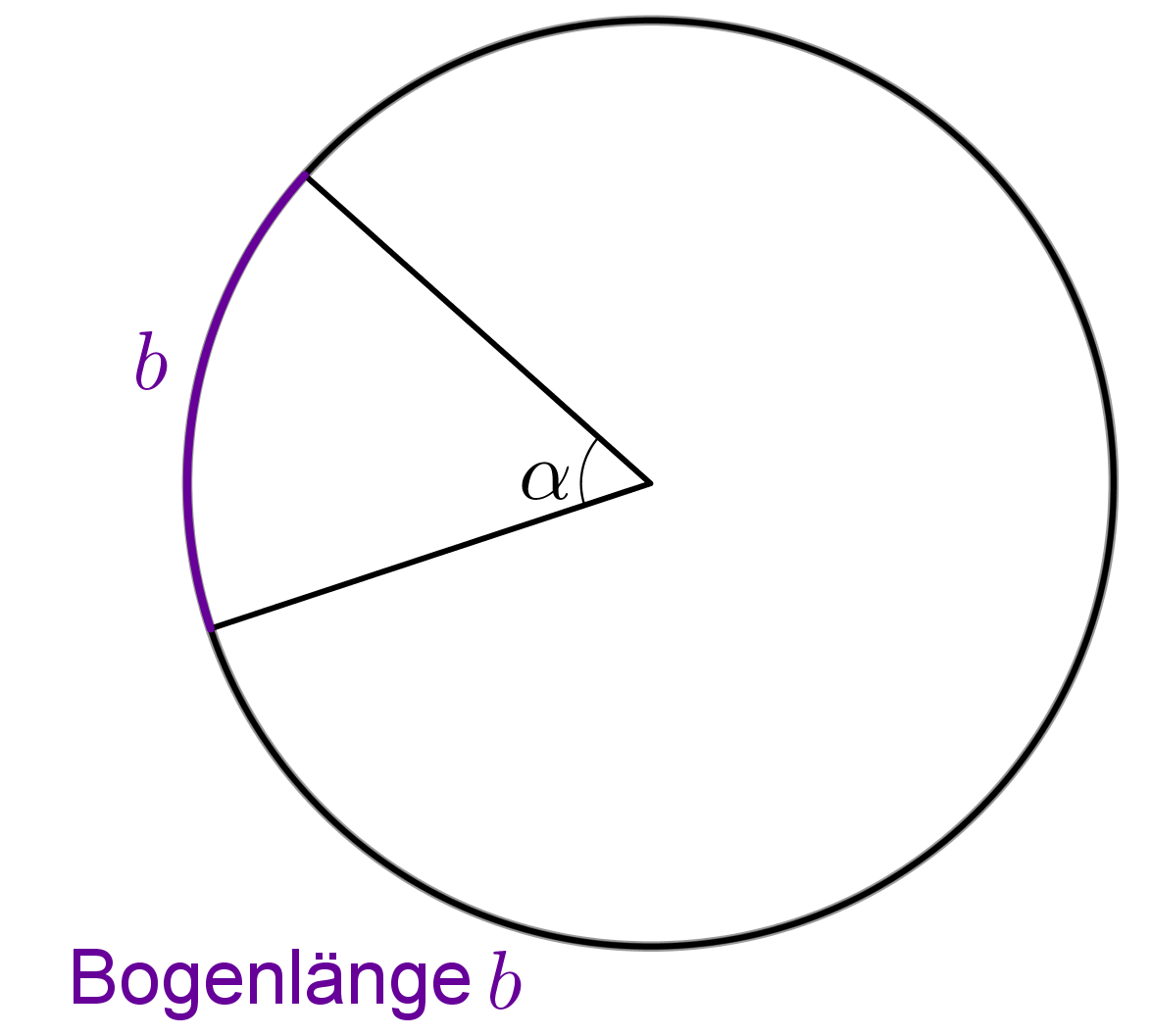
Berechnung der Kreisbogenlänge
Die Kreisbogenlänge kannst du über den vom Kreissektor eingeschlossenen Winkel und den Radius bestimmen.
Der Kreis hat einen Innenwinkel von Das Verhältnis des Winkel zu , gibt dir den Anteil der Kreisbogenlänge vom Umfang an.
Du erhältst so die Formel:
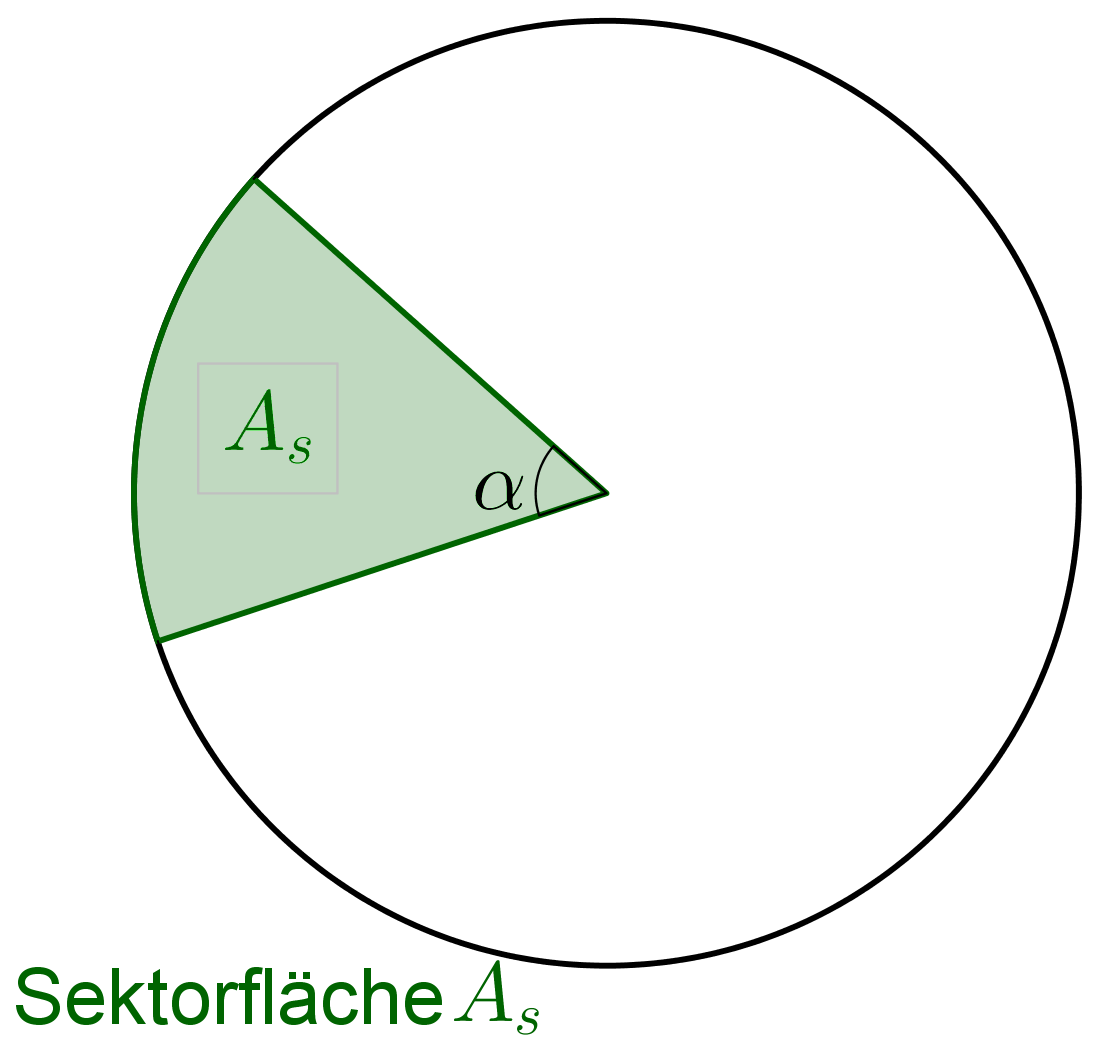
Berechnung der Sektorfläche
Die Sektorfläche bestimmst du auch über das Verhältnis des Winkels zu . Dieses Verhältnis gibt dir an, welchen Anteil der Flächeninhalt vom Kreissektor zum Flächeninhalt des ganzen Kreises hat.
Die Formel zur Berechnung der Sektorfläche lautet also:
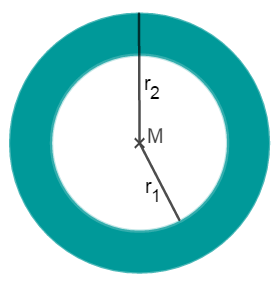
Berechnung des Kreisrings
Ein Kreisring ist die Fläche zwischen zwei Kreisen mit demselben Mittelpunkt.
Hier siehst du zwei Kreise mit dem Mittelpunkt M.
Der kleine Kreis hat den Radius , der große Kreis hat den Radius .
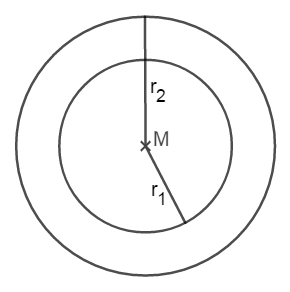
Den Flächeninhalt des Kreisrings berechnest du dadurch, dass du die beiden Kreisflächen voneinander subtrahierst:
Video zur Flächenberechnung
Übungsaufgaben
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zu Kreisen und Kreisteilen
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema: