In diesem Artikel geht es um eine Gruppe besonderer Vierecke, die Rauten.

Eine Raute (manchmal auch "Rhombus" genannt) ist
ein Viereck, bei dem
alle vier Seiten gleich lang sind.
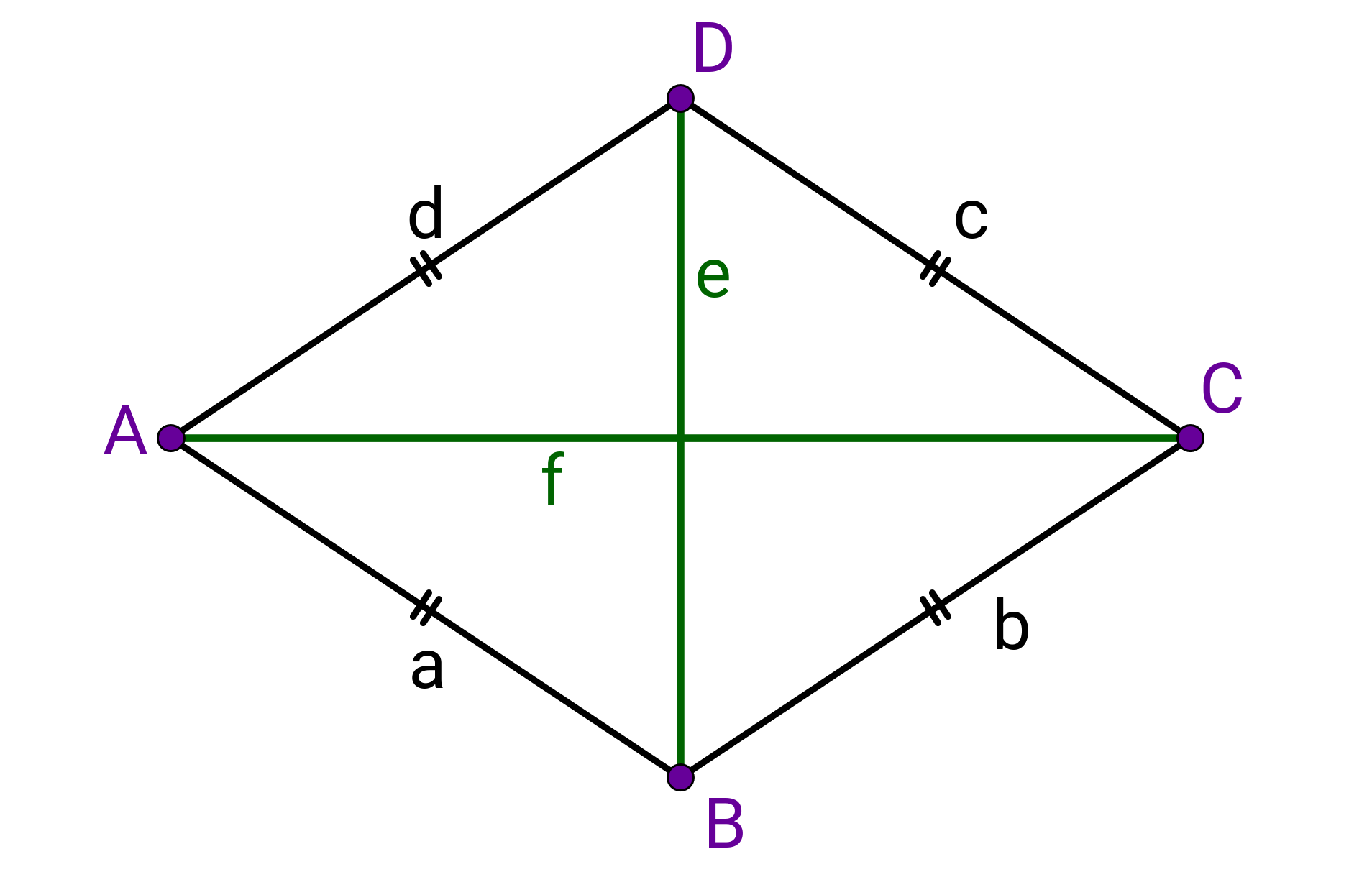
Eigenschaften der Raute
Besonderheiten bei Seiten, Winkeln und Diagonalen
In einer Raute sind gegenüberliegende Winkel immer gleich groß.
Bei einer Raute gilt also:
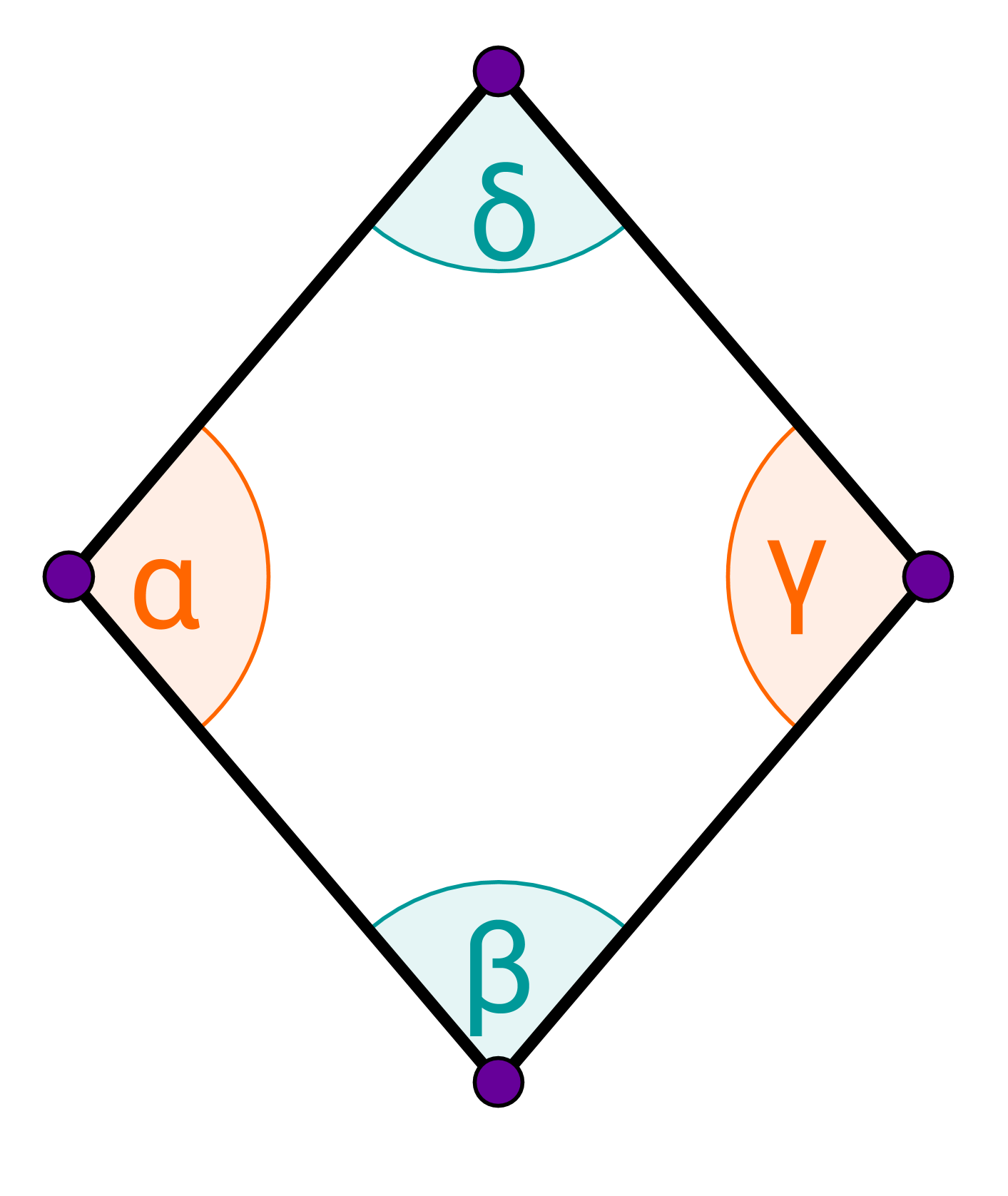
In einer Raute ergeben zwei auf derselben Seite liegende Winkel zusammen immer 180°.
Bei einer Raute gilt also:
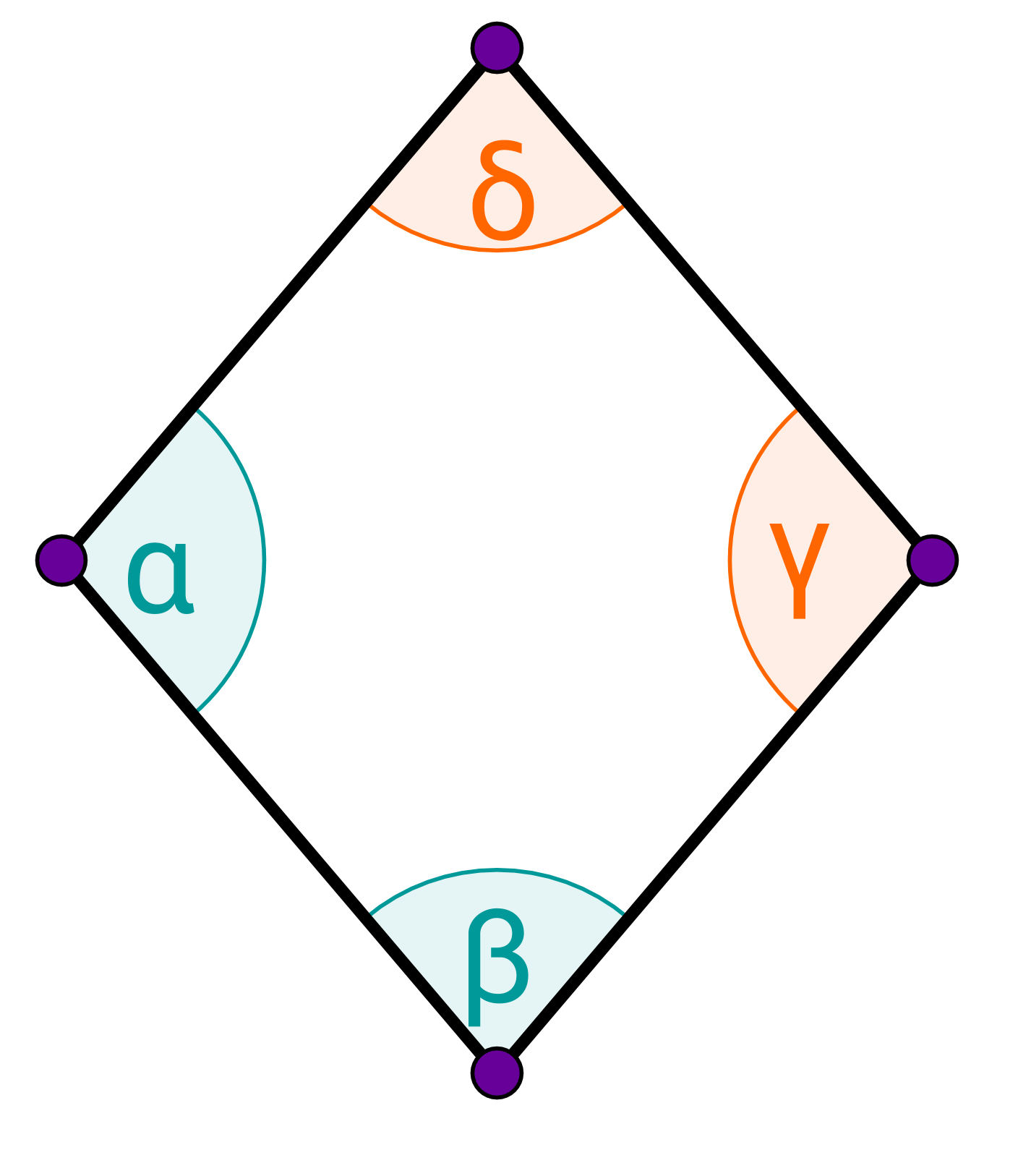
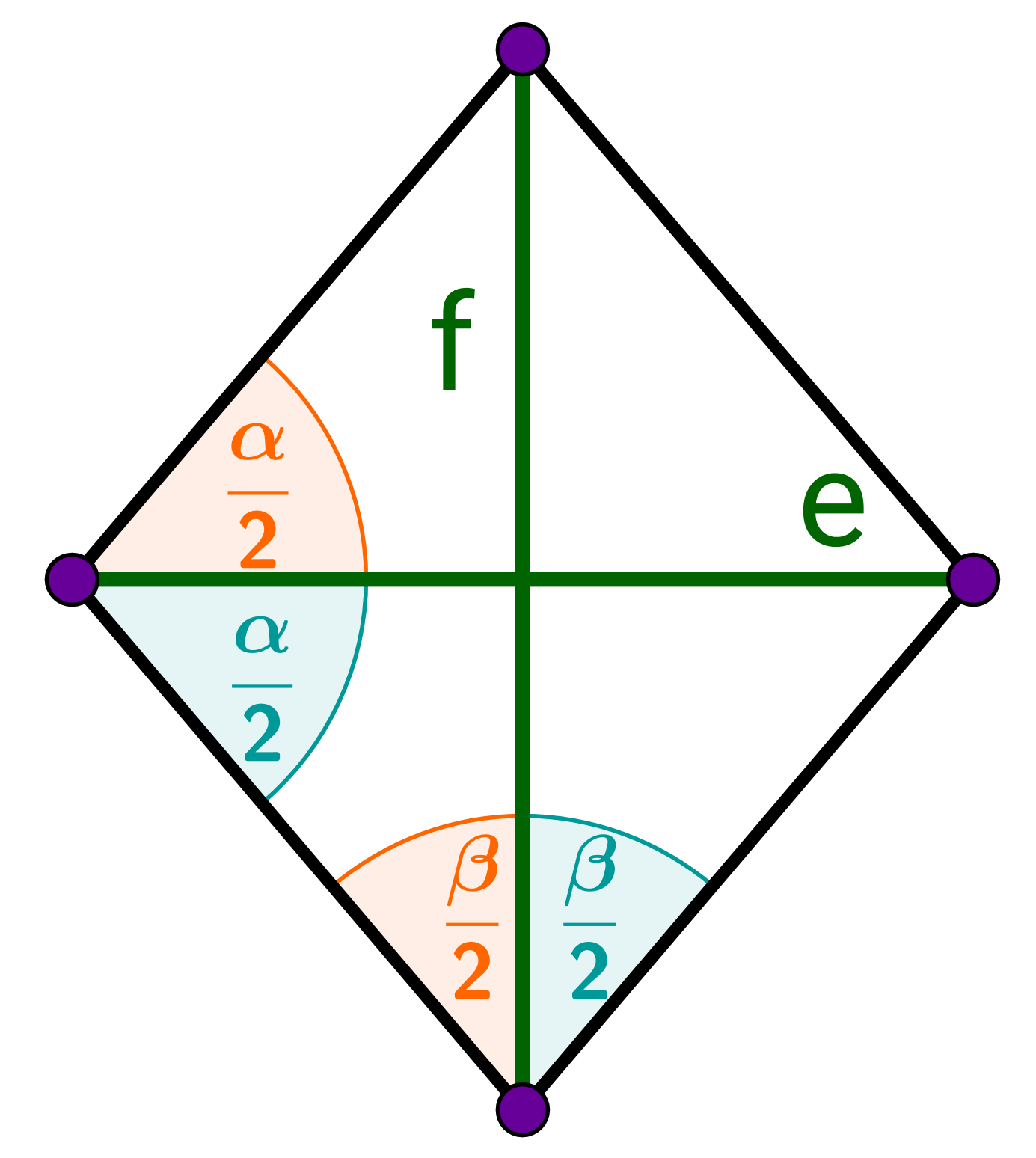
In einer Raute halbieren sich die Diagonalen senkrecht.
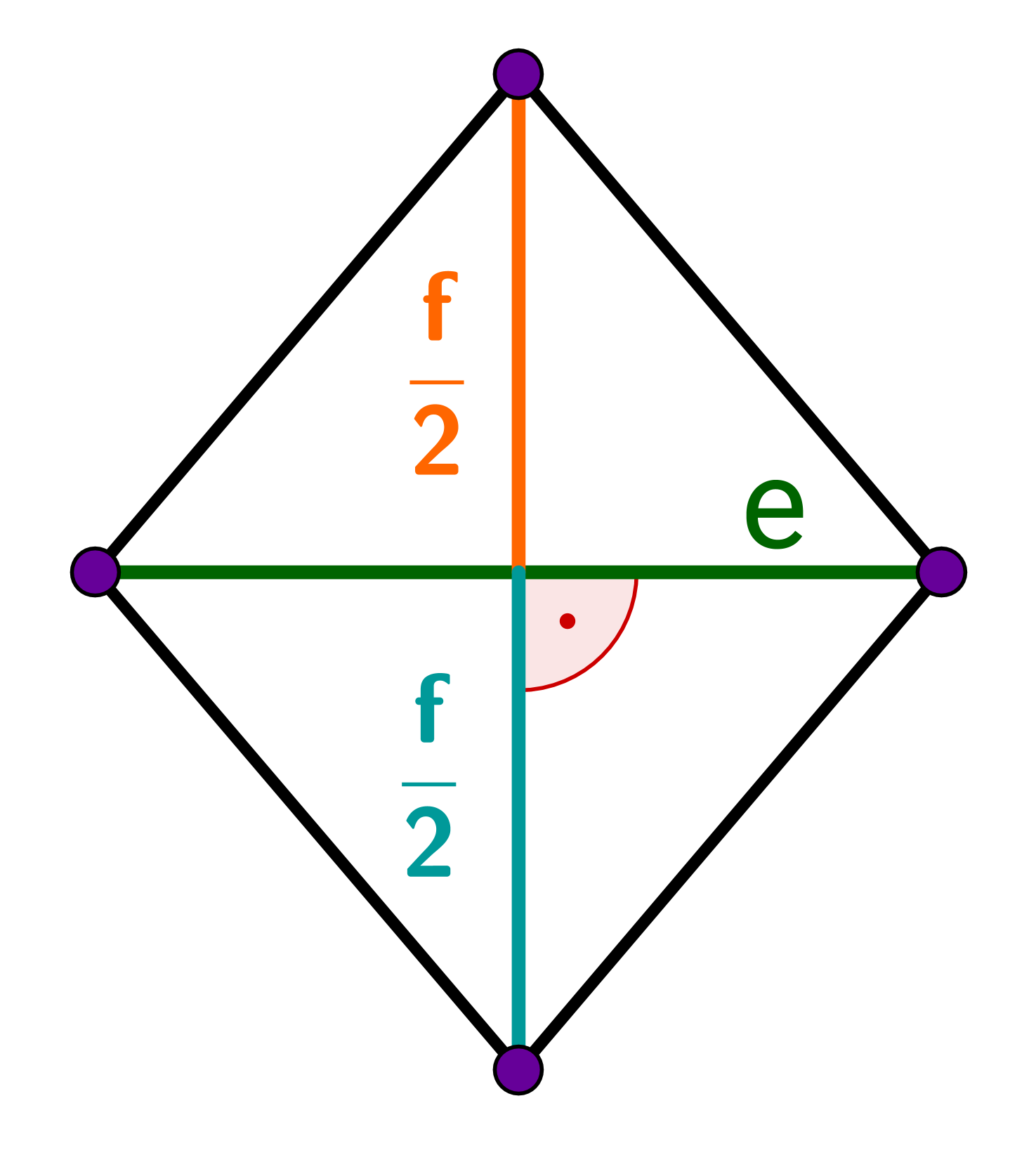
In einer Raute wird jeder Winkel von einer Diagonalen halbiert.
Einordnung als Viereck
Jede Raute ist immer auch ein Trapez, und zwar ein (besonderes) Trapez, bei dem nicht nur ein Paar gegenüberliegender Seiten parallel ist, sondern beide Paare und zusätzlich die Seiten gleich lang sind.
Jede Raute ist immer auch ein Parallelogramm und ein Drachenviereck, und zwar der Sonderfall dieser Viereckstypen mit vier gleich langen Seiten. Ein Viereck ist genau dann eine Raute, wenn es gleichzeitig ein Parallelogramm und ein Drachenviereck ist.
Spezialfälle von Rauten
Wenn eine Raute vier rechte Winkel hat, ist es ein Quadrat.
Wie sich eine Raute im Vergleich zu allen anderen Vierecken verhält, kannst du im Haus der Vierecke sehen.
Symmetrieeigenschaften
Punktsymmetrie
Eine Raute ist immer punktsymmetrisch zum Schnittpunkt der Diagonalen.
Achsensymmetrie
Eine Raute ist immer achsensymmetrisch, mit beiden Diagonalen als Symmetrieachsen.
Umkreis und Inkreis
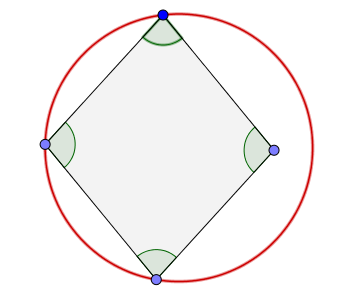
Umkreis: Eine Raute hat im Allgemeinen keinen Umkreis. Ausnahme ist der Sonderfall, wenn die Raute lauter rechte Winkel hat, also ein Quadrat ist.
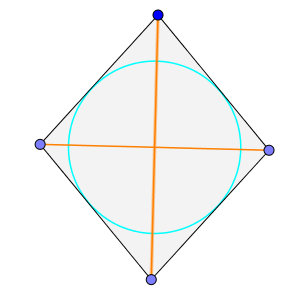
Inkreis: Eine Raute hat immer einen Inkreis. Inkreismittelpunkt ist der Schnittpunkt der Diagonalen.
Flächeninhalt und Umfang
Flächeninhalt:
Der Flächeninhalt einer Raute ist die Hälfte des Produkts der Länge beider Diagonalen:
Wie diese Formel zustande kommt, sieht man im Applet unten. Die Punkte und der Schieberegler lassen sich ziehen.
Umfang:
Der Umfang einer Raute ist die Summe der Seitenlängen. Da alle vier Seiten die gleiche Länge haben, ist der Umfang gegeben durch:
Rauten im Alltag

Die bayrische Flagge enthält viele blaue und weiße Rauten.

Spielkarten der Spielfarbe "Karo" sind rautenförmig.

Das Schild "Vorfahrtsstraße" hat die Form einer Raute.
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
