Um die Lage von bestimmten Punkten zu beschreiben, gibt es Koordinatensysteme. In der Schule benutzt man meist folgende zwei Koordinatensysteme:
zweidimensionales kartesisches Koordinatensystem
dreidimensionales kartesisches Koordinatensystem
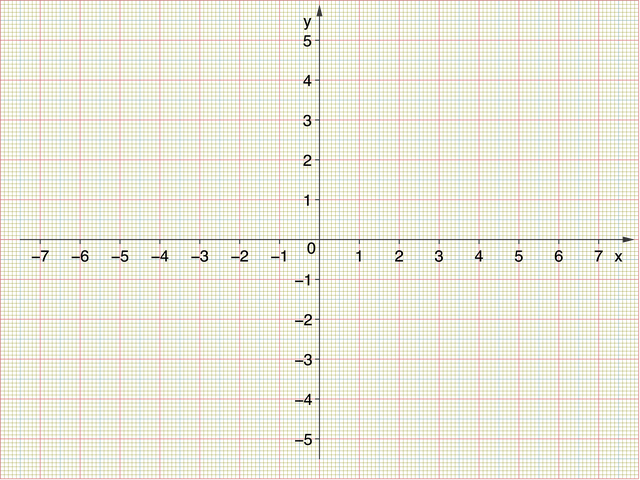
Mithilfe des zweidimensionalen Koordinatensystems kann man Punkte in einer Ebene darstellen, mithilfe des dreidimensionalen Koordinatensystems Punkte im Raum. „Kartesisch“ heißt, dass die Achsen senkrecht aufeinander stehen.
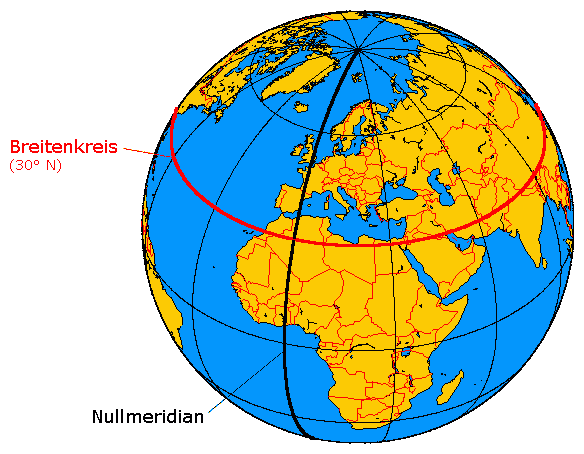
Ein berühmtes Koordinatensystem aus dem Alltag ist das der Erde. Hier kann jede Stadt, jedes Dorf, jeder See… durch die Angabe von Längen- und Breitengrad bestimmt werden.
Mit Koordinatensystemen kann man auch Funktionen graphisch darstellen, oder allgemeiner gesagt: Man kann bildlich darstellen, wie sich zwei Größen zueinander verhalten.
Beispiel:
Du machst bei einem Spendenlauf deiner Schule mit und trägst einen GPS-Sender, der alle vier Minuten deinen Standort an einen PC übermittelt. Dein Sportlehrer trägt die Informationen
zurückgelegte Strecke und
gelaufene Zeit
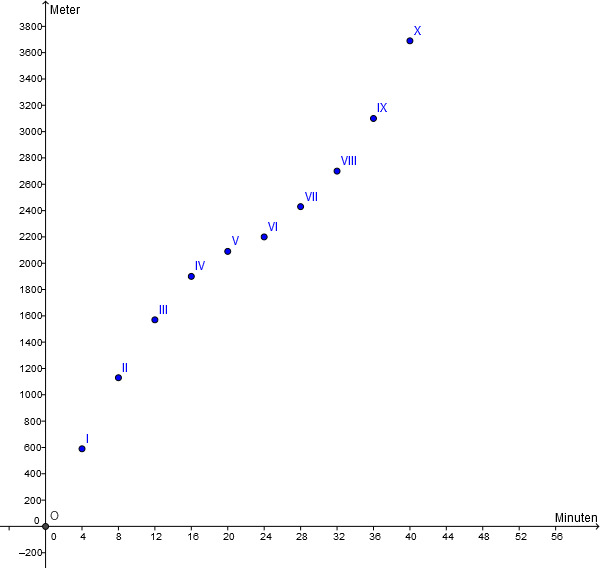
in ein Koordinatensystem ein. Das nennt man auch Weg-Zeit-Diagramm:
Man kann ablesen,
zu welchem Zeitpunkt du welche Strecke zurückgelegt hast,
dass du schnell startest, bis etwa zur Minute langsamer wirst, dann aber wieder an Schnelligkeit gewinnst.
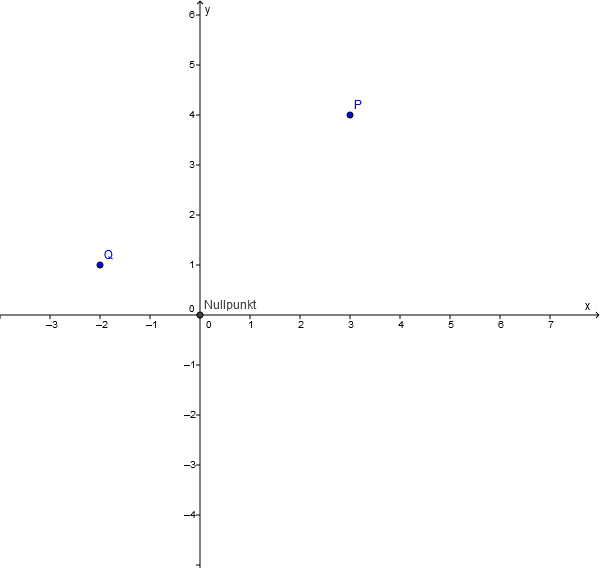
Zweidimensionales Koordinatensystem
Die Lageinformation eines Punktes im zweidimensionalen Koordinatensystem wird in runden Klammern geschrieben und durch einen senkrechten Strich getrennt:
Nullpunkt:
Punkt
Punkt
Zusätzlich kann man von einem Punkt den Quadranten angeben.
Dreidimensionales Koordinatensystem
Um Punkte im Raum zu beschreiben, braucht man drei Informationen:
Wie weit vor oder hinter dem Nullpunkt liegt der Punkt?
Wie weit rechts oder links vom Nullpunkt liegt der Punkt?
Wie weit oberhalb oder unterhalb vom Nullpunkt liegt der Punkt?
Diese drei Informationen bilden die Lageinformation.
Begriffe
Die Richtungen (vorne, hinten, rechts, links, oben, unten) werden durch die Koordinatenachsen - die -, -Achse und -Achse - bestimmt. Manchmal werden sie auch als -, - und -Achse bezeichnet.
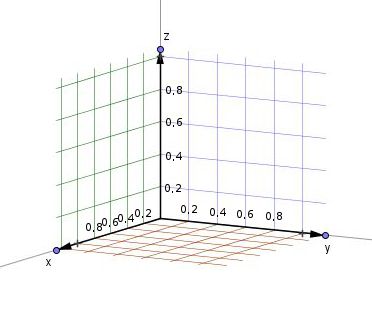
Auch hier ist der Nullpunkt oder auch Ursprung der Schnittpunkt der Koordinatenachsen.
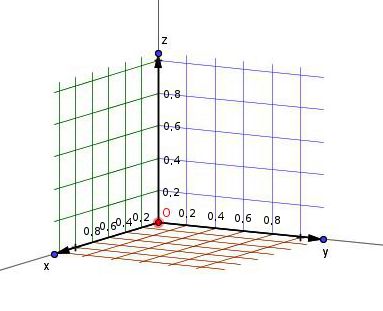
Die Lageinformation eines Punktes wird in runden Klammern geschrieben und durch senkrechte Striche getrennt:
Nullpunkt:
Punkt liegt im Raum und nicht auf dem eingezeichneten Gitter!
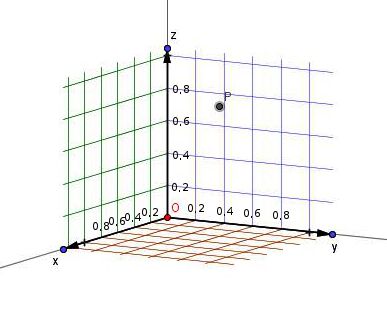
Merke: Die Reihenfolge der Informationen ist festgelegt:
Als Erstes steht die „Vor-Hinter-Information“, die -Koordinate, in der Klammer.
Als Zweites steht die „Rechts-Links-Information“, die -Koordinate, in der Klammer.
Als Drittes steht die „Oben-Unten-Information“, die -Koordinate, in der Klammer.
Allgemein sieht die Notation also so aus: Punkt -Koordinate-Koordinate-Koordinate
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Koordinatensystem
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
